一类具有周期变指数和凹凸非线性项椭圆型方程解的多重性

祁红红, 贾 高

(上海理工大学理学院,上海200093)

一类具有周期变指数和凹凸非线性项椭圆型方程解的多重性

祁红红, 贾 高∗

(上海理工大学理学院,上海200093)

研究一类具有周期变指数和凹凸非线性项的椭圆边值问题,借助Ekeland变分原理和Nehari流形等理论和方法得到解的多重性.

周期变指数;多重性;Nehari流形

§1 引 言

目前,变指数拟线性问题越来越受到人们的关注,国内外许多学者对这一课题进行了研究,并取得一些新的成果,如文献[1-5].

随着弹性力学,流体力学等学科理论的发展激发了对变指数空间的研究,同时变指数Lebesgue空间Lp(x)(RN)和Sobolev空间W1,p(x)(RN)的发展也促进更多物理模型的出现,参见文献[2-4].

T.F.Wu在文献[3]中研究了下面方程多重解的存在性

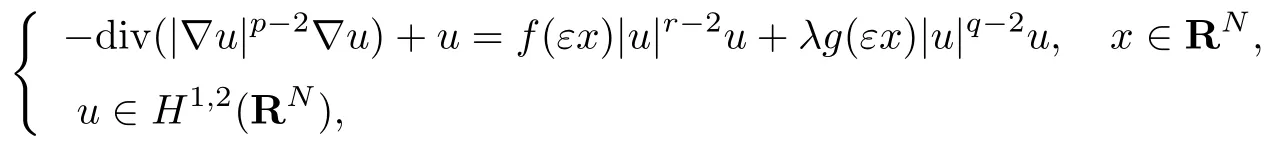
其中q∈(0,1),λ是一个正整数.

T.S.Hsu,H.L.Lin和C.C.Hu在文献[4]中讨论了如下方程

解的存在性和多重性,其中2≤p＜N,N≥3.

在文献[5]中,C.O.Alves等学者研究如下问题解的存在性和多重性

其中λ≥0,k∈N,p(x),q(x),r(x):RN→R是正Lipschitz连续的ZN周期函数,即p(x+z)=p(x),x∈RN,z∈ZN.f(x):RN→ R 是一个正连续函数,存在l个点a1,a2,···,al∈ZN,其中

本文研究含有周期变指数和凹凸非线性项的拟线性椭圆方程解的多重性{

其次,对于问题(1.0)给出一些基本假设:

(F1) p(x),q(x),r(x):RN→R是正Lipschitz连续的ΠN周期函数,且

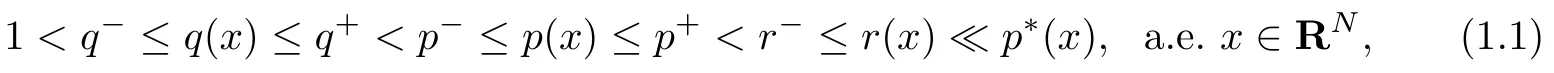
(F3) g(x):RN→R是一个非负可测函数且其中(F4)f(x):RN→ R 是一个正连续函数,存在K个点a1,a2,···,aK∈ ΠN,取a1=0,并且这K个点都是f(x)的极大值点,所对应的极大值为Mi,即Mi=f(ai),1≤i≤K,记M∗=max{Mi,1}.

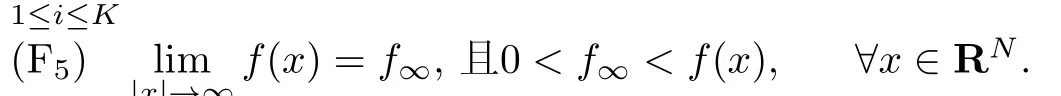
需要特别说明的是,本文研究的边值问题与文献[5]中的相似,本文的工作是将周期性推广到ΠN;将推广到将[5]中关于f(x)具有相等极大值减弱到互不相等极值,在本文主要结论的证明过程中,这是需要克服的最大困难.

本文的主要结果:

定理1.1如果条件(F1)−(F5)满足,那么存在Λ∗＞0,m∗∈N,使得当0＜λ＜Λ∗,m≥m∗时,方程(1.0)至少有K+1个解.

§2 预备知识和主要引理

先介绍变指数空间Lp(x)(RN)和W1,p(x)(RN)的定义和相关性质.

定义Ls(x)(RN)上的范数为函数ρ:Ls(x)(RN)→R为ρ(u)=|u|s(x),可得以下结论:在空间Ls(x)(RN)中,考虑模

命题2.1[5]则

在W1,s(x)(RN)上定义范数为||u||1,s(x)=|u|s(x)+|▽u|s(x),定义模函数为ρ1(u)= ∫(|u|s(x)+|▽u|s(x)).

如果在空间W1,s(x)(RN)上另定义范数

则在W1,s(x)(RN)中||u||1,s(x)和||u||是等价范数([5,7]).在本文的讨论中,只用范数‖·‖.

命题2.2[5]关于‖·‖和ρ1(u)有类似命题2.1的结论.

命题2.3[8](Sobolev嵌入定理) 设s(x):RN→ R 是一个Lipschitz连续函数且1＜s−≤s(x) ≤ s+＜ N,h(x)∈满足s(x) ≤ h(x) ≤ h∗(x),a.e.x ∈ RN,则W1,s(x)(RN)→Lh(x)(RN),且存在常数A＞1,有|v|h(x)≤A||v||,∀v∈W1,s(x)(RN).

根据变分理论,寻求(1.0)的弱解等价于寻找泛函Φλ,m(u):W1,p(x)(RN)→R的临界点

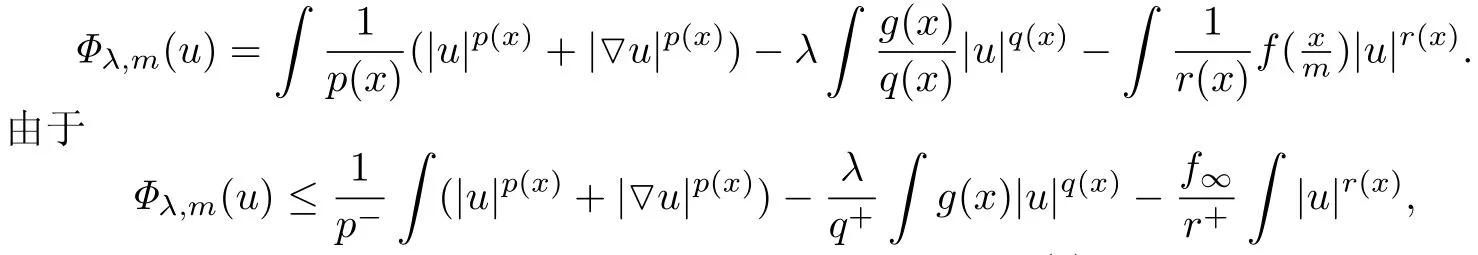
则当||u||→∞时,由(1.1)知Φλ,m(u)→−∞,即Φλ,m(u)在W1,p(x)(RN)上是无下界的,因此不能在W1,p(x)(RN)上借助变分理论研究Φλ,m(u)的临界点的存在性.另一方面,在下面研究中将证明Φλ,m(u)在Nehari流形上是有下界的,所以将在Nehari流形上讨论Φλ,m(u)的临界点.

Nehari流形Nλ,m={u∈W1,p(x)(RN){0}:

则cλ,m是Φλ,m(u)的山路水平数([5]).

当λ=0,f(x)≡P(常数)时,(1.0)成为下列特殊问题{

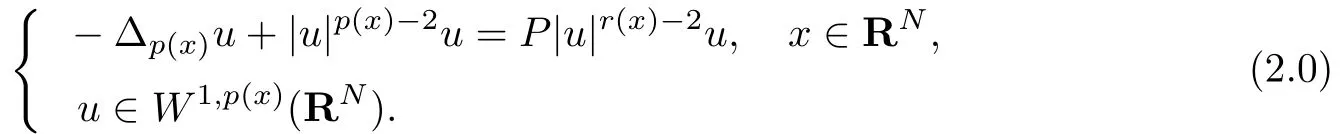
下面将依据引理2.9得到(2.0)解的多重性.

问题(2.0)对应的泛函为ΦP:W1,p(x)(RN)→R,

相应Nehari流形为

引理2.4在Nλ,m上,泛函Φλ,m(u)是强制的并且有下界.

证因为对∀u∈Nλ,m,有Φ′λ,m(u)u=0,从而有

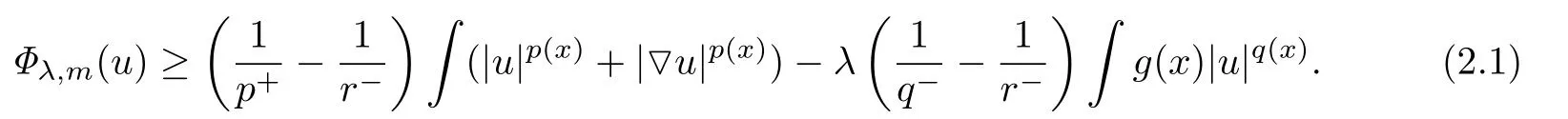
不妨设||u||＞ 1,由H¨older不等式,(F3)和命题2.3得

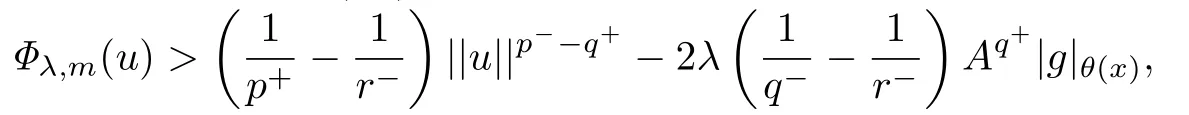
所以当||u||≫1时,上式右端大于0,即Φλ,m(u)在Nλ,m上是强制的并且有下界.

引理2.5假设g满足(F3),{un}⊂ W1,p(x)(RN)是Φλ,m的一个(PS)d序列,那么{un}在W1,p(x)(RN)中是有界的.

此引理的证明是基本的,这里从略.

引理2.6[9]假设g满足(F3),存在{un}⊂W1,p(x)(RN),u∈W1,p(x)(RN),当n→ ∞ 时,有un⇀u和∀v∈W1,p(x)(RN),则存在子列(仍记为{un}),当n→∞时,▽un−→▽u,a.e.x∈RN,对∀v∈W1,p(x)(RN)有

引理2.7若(2.0)中的P取为f(x)的极大值Mi,设在NMi中存在序列{un}满足ΦMi(un)→cMi,则下列两结论只能成立其中之一:(1)在W1,p(x)(RN)中有un→u(n→∞),且u∈ NMi.(2)存在{yn}⊂ΠN且|yn|→+∞(n→n)和w∈W1,p(x)(RN),使得在W1,p(x)(RN)中,wn(x)=un(x+yn)→w(n→∞)和ΦMi(w)=cMi,w∈ NMi.

证由引理2.5知,存在u∈W1,p(x)(RN)及{un}的子列(仍记为{un}),使得在W1,p(x)(RN)中un⇀u.利用Ekeland变分原理,可得

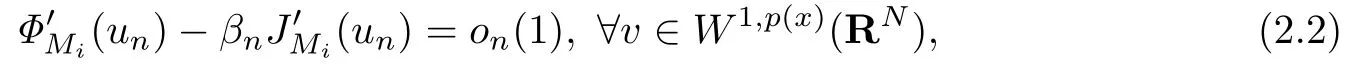
其中{βn}⊂R.因为{un}⊂NMi,那么从(2.2)可知

接下来,证明存在α∗＞0,使得

断言:存在α0＞0,满足||u||＞α0, ∀u∈NMi.

若不然,则存在{vn}⊂NMi,当n→∞时,||vn||→0.因为{vn}⊂NMi,故∫

另一方面,当n充分大时||vn||＜1,由命题2.1-2.2和Sobolev嵌入定理有于是可得这与假设矛盾,故断言成立.

由命题2.2知存在ξ0＞0,使得的定义有故(2.4)得证.

结合(2.3)和(2.4)可得,当n→∞时,成立βn→0,从而

接下来,分u/=0和u=0两种情况进行分析.

情形1:u/=0,a.e.x∈RN.从引理2.6知,当n→∞时,成立

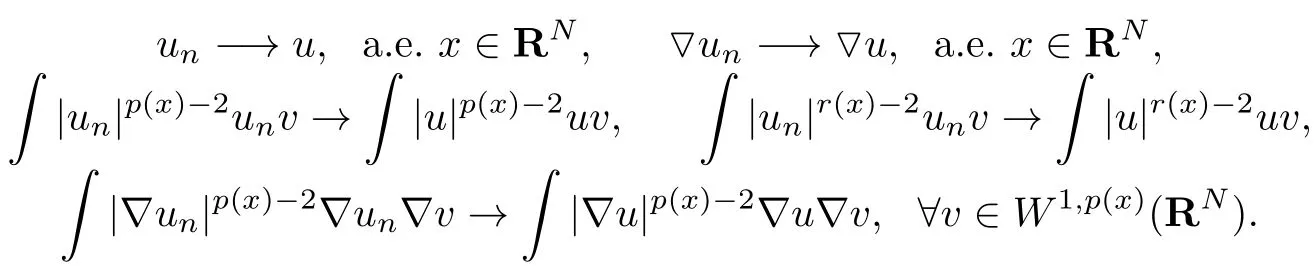
从以上结论可知u是ΦMi的一个临界点.由Fatou引理和引理2.6得

情形2:u=0,a.e.x∈RN.下面证∫明存在R,满足

假设(2.5)不成立,则

由[10]的引理3.1知,在L∫

b(x)(RN)中un→0,其中b(x)∈C(RN)且p(x)≪b(x)≪p∗(x).由

,则在W1,p(x)(RN)中un→ 0,故cMi=0.

又因为对v ∈ N 有(|v|p(x)+|▽v|p(x))=M|v|r(x),而

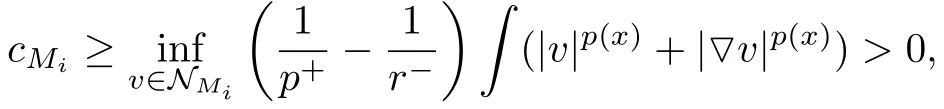
即cMi＞0,显然矛盾,故断言成立.

设{yn}⊂ΠN且|yn|→+∞,定义wn(x)=un(x+yn).因为p(x),q(x)和r(x)都是ΠN周期函数,经变量代换后得Φ于是{wn}是ΦMi的一个(PS)cMi序列.由引理2.5知{wn}在W1,p(x)(RN)中是有界的,于是在W1,p(x)(RN)中有wn⇀w. 由(2.5)得则w/=0.

对{wn}重复(1)的步骤,可得在W1,p(x)(RN)中有wn→w和ΦMi(w)=cMi,w∈NMi.

引理2.8对任意m ∈ N,则存在正常数λ0＞ 0,α和l,当λ ∈ (0,λ0),||u||=l时,有Φλ,m(u)≥α＞0.

证由H¨older不等式,(F3)和Sobolev嵌入定理得

不妨设||u||＜1,由命题2.1和Sobolev嵌入定理得

因为p+＜r−,选取充分小的l,使得

另一方面,选取λ0满足在∂Bl(0)上有

引理2.9[5]设(F3),(F4)和(1.1)满足,记则对

由引理2.9,当0＜ λ ＜ Λ1时,下面的几个引理将给出的一些重要性质.依据引理2.9还可以得到:

引理2.10设0＜λ＜Λ1,则下列不等式成立:

证明省略之.

引理2.11(1)设(F3)满足,则有一常数0,使得对成立Φλ,m(u)＞ L;(2)设(F2),(F3),(F5)和(2.1)满足,如果0＜ λ ＜ Λ1,那么对任意有Φλ,m(u)＜0,并且

利用Young不等式可得

§3 主要结论的证明

引理3.1[11](1)在Nλ,m中存在Φλ,m的一(PS)γλ,m序列;(2)在中存在Φλ,m的序列;(3)在中存在Φλ,m的一序列.

引理3.2[5]设单调递增的连续函数fl:[0,+∞)→[0,+∞),fl(0)=0,(l=1,2,3),且满足

(2)函数φ=f1−f3在[0,+∞)中只有一个极大值点,并且当t→+∞时,φ(t)→−∞,

那么存在λ1＞0,当0＜λ＜λ1时,ψ=f1−λf2−f3只有两个正的零点.

借助引理3.2,可以得到下列引理:

引理3.3对u∈W1,p(x)(RN){0},那么下列结论成立:

(1)若∫g(x)|u|q(x)=0,则存在t−＞0,使得(2)若0＜λ ＜ Λ1,∫g(x)|u|q(x)＞ 0,则存在正数t∗,t+,t−满足t+＜ t∗＜ t−,使得,且

证设u∈W1,p(x)(RN){0},通过计算有

令φ(t)=Φλ,m(tu),∀t∈[0,+∞),则φ(0)=0.如果g(x)|u|q(x)=0,当0＜t≪ 1时,

当t≫ 1时,可得φ(t)＜ 0. 于是存在t−＞ 0,使得进一步有结合(3.3)可推出令v=t−u,则

下面∫证明(2).令

容易验证I1(t),I2(t)和I3(t)满足引理3.2的条件,函数ψ(t)=I1(t)−λI2(t)−I3(t)有两个正的零点,t+＜ t−.对φ(t)= Φλ,m(tu),因为φ(0)=0,如果∫g(x)|u|q(x)＞ 0,那么当0＜ t≪ 1时,φ(t)＜0,于是φ(t)在t=t+处有一个局部最小值.因此,故利用引理2.11(2)有Φλ,m(t+u)＜ 0,即φ(t+)＜ 0.

因为t+和t−是φ(t)仅有的两个临界点,并且t+,t−∈ (0,1),于是可知φ(t)在t=t−处有一个局部最大值,那么故根据引理2.11(1)有Φλ,m(t−u)＞0,即φ(t−)＞ 0.因此φ(t)在区间(t+,t−)上存在唯一的零点t∗,从而

引理3.4设D∗(λ)由引理2.12给出,条件(F3)和(F5)满足,当0＜ λ ＜ Λ1时,则泛函Φλ,m满足(PS)d条件,其中d ＜ cf∞−D∗(λ).

证设{vn}⊂ W1,p(x)(RN)是Φλ,m的一(PS)d序列,其中d＜ cf∞−D∗(λ).从引理2.5知{vn}在W1,p(x)(RN)中是有界的,即存在一个子列(仍记为{vn}),在W1,p(x)(RN)中有vn⇀ v(n→∞).由引理2.6知由引理2.8知Φλ,m(v)≥0,且wn=vn−v是Φ0,m的一个(PS)d∗序列,其中d∗=d−Φλ,m(v)＜ cf∞,(见引理2.12).

下面证明存在R＞0,使得

假设(3.4)不成立,则对∀R＞0,存在ξ2＞0,{yn}⊂ΠN满足

故¯w是问题(2.0)的弱解.又因为

这与d∗＜ cf∞矛盾,故(3.4)成立.

引理3.5如果条件(F3)和(F5)满足,对于Λ∗∈(0,Λ1),使得当λ ∈(0,Λ∗)时,问题(1.0)至少有一个基态解

证根据引理3.1(1)知,存在Φλ,m的一个极小化序列{un}⊂Nλ,m,且有Φλ,m(un)=γλ,m+on(1),因为cf∞＞0,存在0＜ Λ∗＜ Λ1,则对∀λ ∈(0,Λ∗)有γλ,m＜0＜cf∞−D∗(λ).从引理3.4可知,存在{un}的一个子列(仍记为{un})和u∗∈ W1,p(x)(RN),使得un→u∗(W1,p(x)(RN)),于是u∗是(1.0)的一个弱解,并且Φλ,m(u∗)= γλ,m＜ 0.

于是由γλ,m的定义得这与γλ,m＜ 0矛盾.

由引理3.3(2)知,存在t+＜t−=1,使得且

根据泛函Φλ,m(u),Φ0,m(u),Φf∞(u),ΦMi(u)的特征及水平(山路)cλ,m,c0,m,cf∞,cMi, 容易得到下列结论:

引理3.6(1)对任意i,j ∈ {1,2,···,K},i/=j,如果Mi/=Mj,那么cMi/=cMj;(2)对极小水平数cMi和cf∞有cMi＜ cf∞成立.

证明省略之.

由假设(F4),那么存在ρ0＞0,r0＞0且满足下列条件:

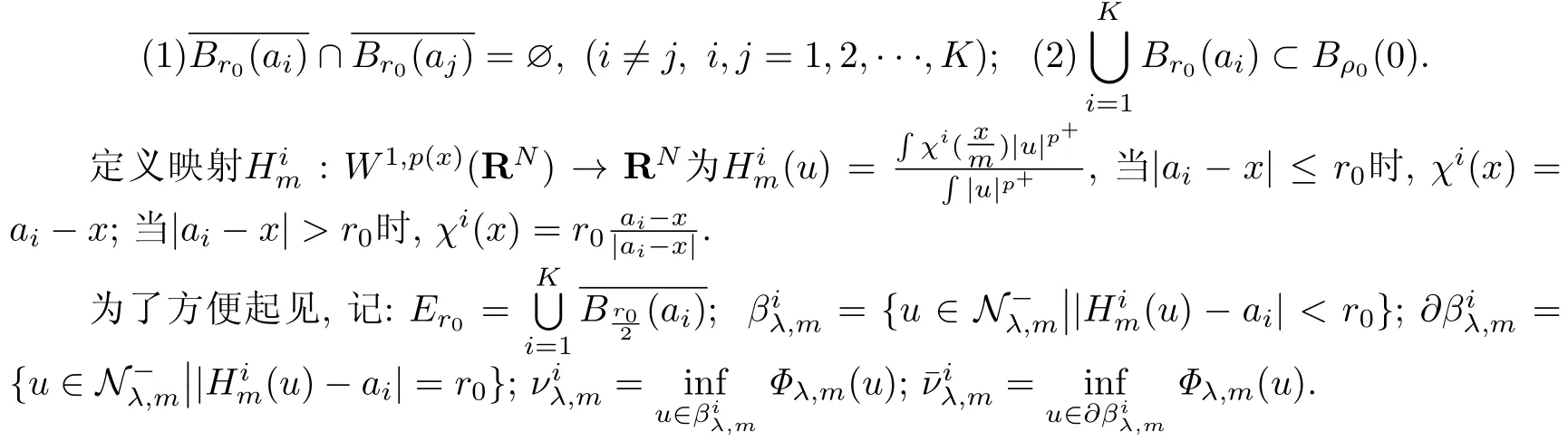
引理3.7若(F1-F2)满足,则在NMi中存在{un},使得∞).

证利用证明引理2.4的方法可得ΦMi(u)在NMi上有下界.

下面证明ΦMi(u)在NMi上是弱下半连续的.

设在NMi上un⇀ u,则{un}有界,于是存在子列(仍记为{un}),在Lh(x)(RN)(h(x)＜p∗(x))上un→u和un→u,a.e.x∈RN,所以(u)u=0.由Fatou引理可得

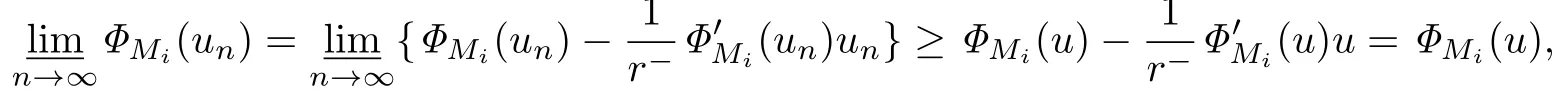
故ΦMi(un)在NMi上是弱下半连续的.因此,由Ekeland变分原理可得在NMi上存在{wn},使得ΦMi(wn)→cMi,

引理3.8对f(x)的极大值Mi,那么存在充分小的ε0＞0和充分大的m0＞0,当m≥m0,对任意的u∈N0,m且满足cMi−ε0≤Φ0,m(u)≤cMi+ε0,有

证由引理3.7可知在NMi上存在{wn},使得ΦMi(wn)→cMi,→0,n→ ∞.对于wn∈NMi有令φ(t)=当0＜t≪1时,φ(t)＞0,当t→+∞时,φ(t)＜0,所以必存在tn＞0,使得Φ即tnwn∈N0,m.

用反证法.假设此引理结论不成立,则存在εn→0,mn→+∞(n→∞),un=tnwn∈N0,mn,使cMi− εn ≤ Φ0,mn(un)≤ cMi+εn,但

根据引理2.7,有以下两种情况之一:

(1)在W1,p(x)(RN)中有nun→u0,且u0∈NMi(n→∞).

(2)存在{yn}⊂ΠN,|yn|→+∞(n→∞),使得在W1,p(x)(RN)中,vn=nun(x+yn)→v0(n→∞)和ΦMi(v0)=cMi,v0∈ NMi.

对于情况(1):由Lebesgue控制收敛定理得

因为ai∈Er0,所以当n充分大时,这与(3.5)矛盾.

对于情况(2):由N0,mn定义以及Ekeland变分原理可得可知对G∈W1,p(x)(RN)有那么

因为在W1,p(x)(RN)中vn→ v0(n→ ∞),所以{vn}有界,则在W1,p(x)(RN)中vn⇀ v0和vn→v0,a.e.x∈RN,从引理2.6知∇vn→∇v0,a.e.x∈RN.

即v0是(2.0)的一个非平凡弱解.由Fatou引理得

这与引理3.6(2)的结论cMi＜cf∞矛盾.

如同(3.7)式,可得cf(y0)≤ cMi,其中cf(y0)是Φf(y0)(u)的山路水平.由cMi−εn≤ Φ0,mn(un)≤cMi+εn,可知0≤Mi−f(y0)＜ε,其中ε为充分小的正数.如果f(y0)＜Mi,那么可得cf(y0)＞cMi,这与cf(y0)≤cMi矛盾.于是f(y0)=Mi,故y0=ai.由Lebesgue控制收敛定理

综合(1)和(2)可知引理成立.

引理3.9设ε0和m0是引理3.8中给出的,令

那么当m≥m0,λ∈[0,Λ)时,存在R1,R2＞0,使得

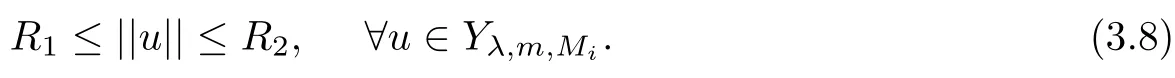
不妨设||u||＞1,因为q+＜p−,所以存在R1,R2＞0,使得R1≤||u||≤R2,∀u∈Yλ,m,Mi.

引理3.10设u∈Yλ,m,Mi,tu≥0满足tuu∈N0,m,Λ＞0由引理3.9中给出,那么存在m′＞0和R＞0,当λ∈[0,Λ],m≥m′时,对任意u∈Yλ,m,Mi成立0≤tu≤R.

证用反证法.假设结论不成立,则存在un∈Yλn,mn,Mi,λn→0,mn→+∞(n→∞),使得tunun∈N0,mn且tu∫n→+∞.不妨设tun≥1,由tunun∈N0,m∫n和0＜f∞＜f(x)可得

下面证明存在η1＞0,使得 ∫

假设(3.10)不成立,即存在{un}的一个子列(仍记为{un}),使|un|r(x)=on(1)(n→∞).

因为un∈Yλn,mn,Mi,所以

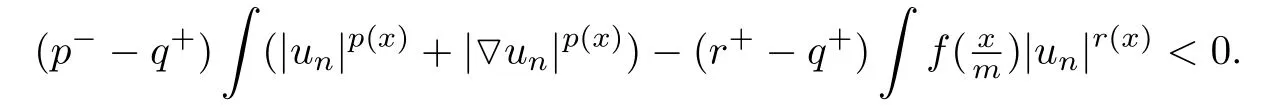
结合(3.8)知,存在C1,C2＞0,使得C1＜ρ1(un)＜C2,那么

这与p−＞ q+矛盾,故(3.10)成立. 从而由(3.9)得即{un}是无界序列.而由引理3.9知{un}是有界的,故反证法假设不成立,引理得证.

引理3.11令m♯=max{m0,m′},则存在Λ♯＞ 0,当m ≥ m♯,λ ∈ [0,Λ♯]时,对任意u ∈Yλ,m,Mi,成立Him(u)∈ Er0.

证设u∈Nλ,m,存在tu＞0满足tuu∈N0,m,则

由(F3),引理3.10和H¨older不等式可得

因为u ∈ Yλ,m,Mi,故

对f(x)的极大值Mi,由引理2.7知(2.0)有一个基态解Vi∈W1,p(x)(RN),使得ΦMi(Vi)=cMi,对Vi,若定义函数则有下列引理:

引理3.12对f(x)的极大值Mi,那么有

证因为p(x),q(x)和r(x)是ΠN周期函数,并且ai∈ΠN,变量代换可得

从上式可知存在ti,m＞0,α＞0(见证引理2.8),使得

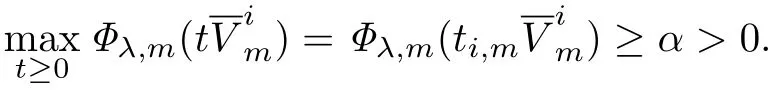
于是当m → ∞时,ti,m↛ 0且ti,m↛ ∞,从而{ti,m}是有界数列,则数列{ti,m}必存在收敛子列(仍记为{ti,m}),即ti,m→t0∫＞0(m→ ∞).因此,由Lebesgue控∫制 收敛定理得

引理3.13设Λ♯,m♯由引理3.11给出,D∗(λ)是引理2.12给出,则存在Λ∗∈ (0,Λ♯),m∗＞m♯,当λ ∈[0,Λ∗),m≥m∗,时,成立

证由引理3.6(2)可知存在Λ∗∈ (0,Λ♯),使得对任意λ ∈ [0,Λ∗)满足cMi＜ cf∞−D∗(λ).取ε¯ ∈(0,ε0)(ϵ0是由引理3.8给出),使cMi+ε¯＜cf∞−D∗(λ).因为

另一方面,结合引理3.12知,当m充分大,对λ∈[0,Λ∗)成立于是当m∗＞m♯时,成立

引理3.14[12]对f(x)的极大值Mi,则泛函Φλ,m存在一个(PS)νλi,m序列

引理3.15假设(F1−F5)满足,则存在Λ∗＞ 0,m∗＞ 0,对λ ∈ [0,Λ∗),m ≥ m∗,在

中(1.0)至少有K个弱解.

证依据引理3.14知在中,泛函Φλ,m存在一个(PS)νλi,m序列由引理3.13得再由引理3.4知在W1,p(x)(RN)中0,即ui是(1.0)的一个弱解.

定理1.1的证明结合引理3.5和引理3.15可得定理1.1.

[1] Alves C O.Existence of solution for a degenerate p(x)-Laplacian equation in RN[J].Journal of Mathematical Analysis and Applications,2008,345(2):731-742.

[2] Musielak J.Orlicz Spaces and Modular Spaces[J].Lecture Notes in Mathematics,1983,1034(4):1-216.

[3] Wu Tsungfang.Multiplicity of positive solutions for semilinear elliptic equations in RN[J].Proceedings of the Royal Society of Edinburgh:Section A Mathematics,2008,138(12):674-670.

[4] Hsu Tsingsan,Lin Hueili,Hu Chungche.Multiple positive solutions of quasilinear elliptic equations in RN[J].Journal of Mathematical Analysis and Applications,2012,388(4):500-512.

[5] Alves C O,Barreiro J L P,Goncalves J V A.Multiplicity of solutions of some quasilinear equations in RNwith variable exponents and concave-convex nonlinearities[J].arXiv:1409.0910[math.AP],2014.

[6] Willem M.Minimax Theorems[A].Progress in Nonlinear Di ff erential Equations and Their Applications,24[C].Berlin:Springer-Verlag,1996.

[7] Kov´a˘cik O,R´akosnik J.On spaces Lp(x)(Ω )and Wk,p(x)(Ω )[J].Czechoslovak Mathematical Journal,1991,41(4):592-618.

[8] Diening L,Harjulehto P,H¨ast¨o P,Ruzicka M.Lebesgue an Sobolev Spaces with variable exponents[A].Lecture Notes in Mathematics,2017[C].Heidelberg:Springer-Verlag,2011.

[9] Qi Honghong,Jia Gao.Existence and multiplicity of solutions for quasilinear p(x)-Laplacian equations in RN[J].Journal of Applied Mathematics and Physics,2015,10(3):1270-1281.

[10]Fan Xianling,Zhao Yuanzhang,Zhao Dun.Compact embedding theorems with symmetry of Strauss-Lions type for the space W1,p(x)(RN)[J].Journal of Mathematical Analysis and Applications,2001,255(1):333-348.

[11]Miotto M L,Miyagaki O H.Multiple positive solutions for semilinear Dirichlet problems with sign-changing weight function in in fi nite strip domains[J].Nonlinear Analysis,2009,71(7):3434-3447.

[12]Lin Hueili.Multiple positive solutions for semilinear elliptic systems[J].Journal of Mathematical Analysis and Applications,2012,391(1):107-118.

Multiplicity of solutions for a class of quasilinear elliptic equations with periodic variable exponents and concave-convex nonlinearities

QI Hong-hong,JIA Gao
(College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)

The boundary value problems of a class of quasilinear elliptic equations are considered,which possess periodic variable exponents and concave-convex nonlinearities in RN.Under some weaker assumptions,the multiplicity of solutions for the equations is obtained by applying the Ekeland’s variational principle and the Nehari manifold theory.

periodic variable exponent;multiplicity;Nehari manifold

35J62;58E05;35J20

O175.25

A

:1000-4424(2016)03-0294-13

2016-01-19

2016-05-23

*通讯作者,Email:gaojia89@163.com

国家自然基金(11171220);上海市一流学科(系统科学)项目(XTKX2012);沪江基金(B14005)