寿命为爱尔兰分布的可修闭路排队模型时间依赖解的渐近性质

阿力木·米吉提

(新疆广播电视大学远程教育学院,新疆乌鲁木齐830049)

寿命为爱尔兰分布的可修闭路排队模型时间依赖解的渐近性质

阿力木·米吉提

(新疆广播电视大学远程教育学院,新疆乌鲁木齐830049)

利用C0-半群理论研究寿命为爱尔兰分布的可修闭路排队系统.首先利用泛函分析中的Hille-Yosida定理,Phillips定理和Fattorini定理证明此排队系统模型正时间依赖解的存在唯一性.然后通过研究该模型相应主算子的谱的特征,分别得到虚轴上除了0外其他所有点都属于该模型主算子的豫解集与0是其主算子及其共轭算子的几何重数为1的特征值.最后将上述结果结合在一起推出该模型的时间依赖解强收敛于其稳态解.

C0-半群;dispersive算子;特征值;豫解集;几何重数

§1 引 言

可修系统模型是可靠性理论中的重要的研究对象之一,有着广泛的应用.正因为有强烈的应用背景,许多学者不断的研究它[1-3].1997年朱翼隽[4]在以前学者工作的基础上,以实际应用作为背景,将闭路可修排队系统中服务设备的寿命从指数分布推广到爱尔兰分布,用补充变量法建立了寿命为爱尔兰分布的可修闭路排队模型，并在

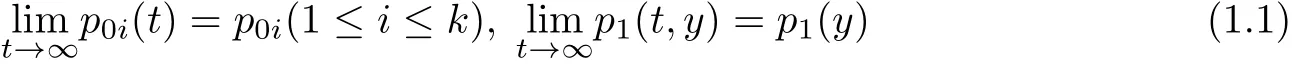
的情况下,进一步获得了该模型稳态下的循环时间,同时求得了此模型可修相位上的平均失效次数及稳态故障频度.实际上(1.1)中隐含了如下两个假设：

1.该排队模型有唯一的正时间依赖解p(t,y);

2.此时间依赖解p(t,y)在给定的初始条件下趋向于其稳态解p(y),其中

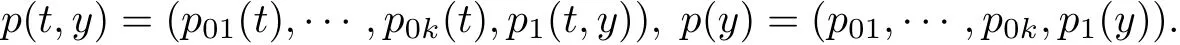
本文运用强连续算子半群理论对寿命为爱尔兰分布的可修闭路排队模型进行动态分析,即证明上述两个假设的成立.为此,首先将通过引入状态空间,主算子及其定义域,把寿命为爱尔兰分布的可修闭路排队模型转化为Banach空间中的抽象Cauchy问题.然后运用Hille-Yosida定理,Phillips定理和Fattorini定理证明该模型正时间依赖解的存在唯一性,即推出假设1的合理性.最后通过研究该模型相应主算子的谱的特征得到此模型时间依赖解的渐近行为,即,首先证明0是此模型主算子的几何重数为1的特征值,然后通过利用文献[5]中的边界扰动思想获得该模型主算子的豫解集,并推出虚轴上除了0外其它所有点都属于此模型主算子的豫解集,最后求出该模型主算子的共轭算子表达式并证明0是该共轭算子的几何重数为1的特征值,由此推出寿命为爱尔兰分布的可修闭路排队模型的时间依赖解强收敛于其稳态解,即得到假设2的成立.

§2 模型的转换

由文献[4],寿命为爱尔兰分布的可修闭路排队模型用以下微积分方程组描述:

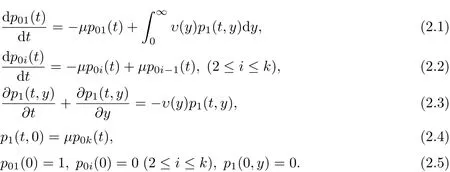
其中(t,y)∈[0,∞)×[0,∞);p0i(t)(1≤i≤k)表示在时刻t系统中孔加工中心未失效,并孔加工中心正启用第i−1组备用刀具的概率；p1(t,y)表示在时刻t系统中孔加工中心故障失效且已消耗的刃磨修理时间为y的概率;µ表示孔加工中心每组刀具的平均寿命;k表示孔加工中心刀具的数量;υ(y)表示故障部件的刃磨修复率.

则方程(2.1)-(2.5)可以描述为Banach空间X上的一个抽象Cauchy问题:

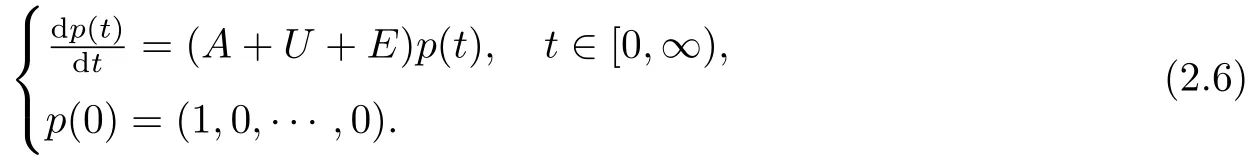
§3 系统(2.6)的适定性

定理3.1则A+U+E生成一个正压缩C0-半群T(t).

证分四步证明此定理.第一步估计A的豫解式.第二步验证D(A)在X中的稠密性.第三步指出U和E为有界线性算子,并推出A+U+E生成一个C0-半群T(t).最后由算子的耗散性和Phillips定理得到T(t)是一个正压缩C0-半群.

对给定的x=(x01,x02,···,x0k,x1(y))∈ X,考虑方程(γI −A)p=x,即

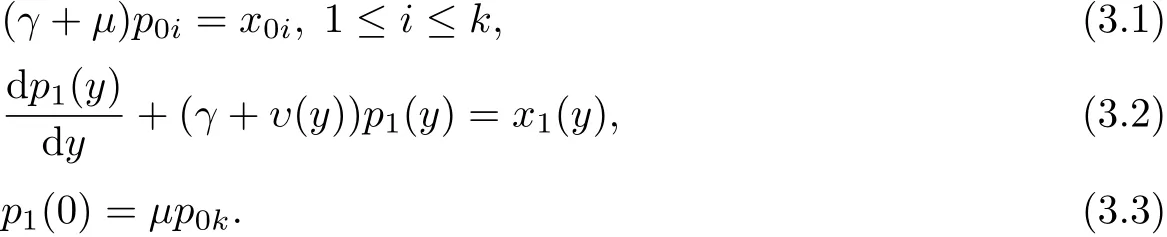
解方程(3.1)-(3.3)算出

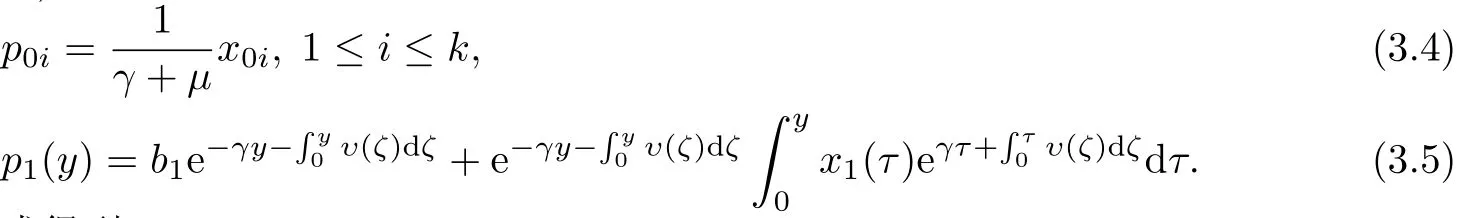
由(3.3)与(3.5)式得到

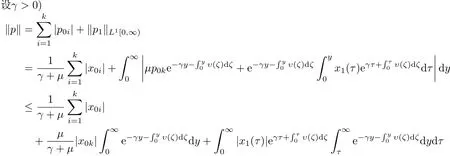
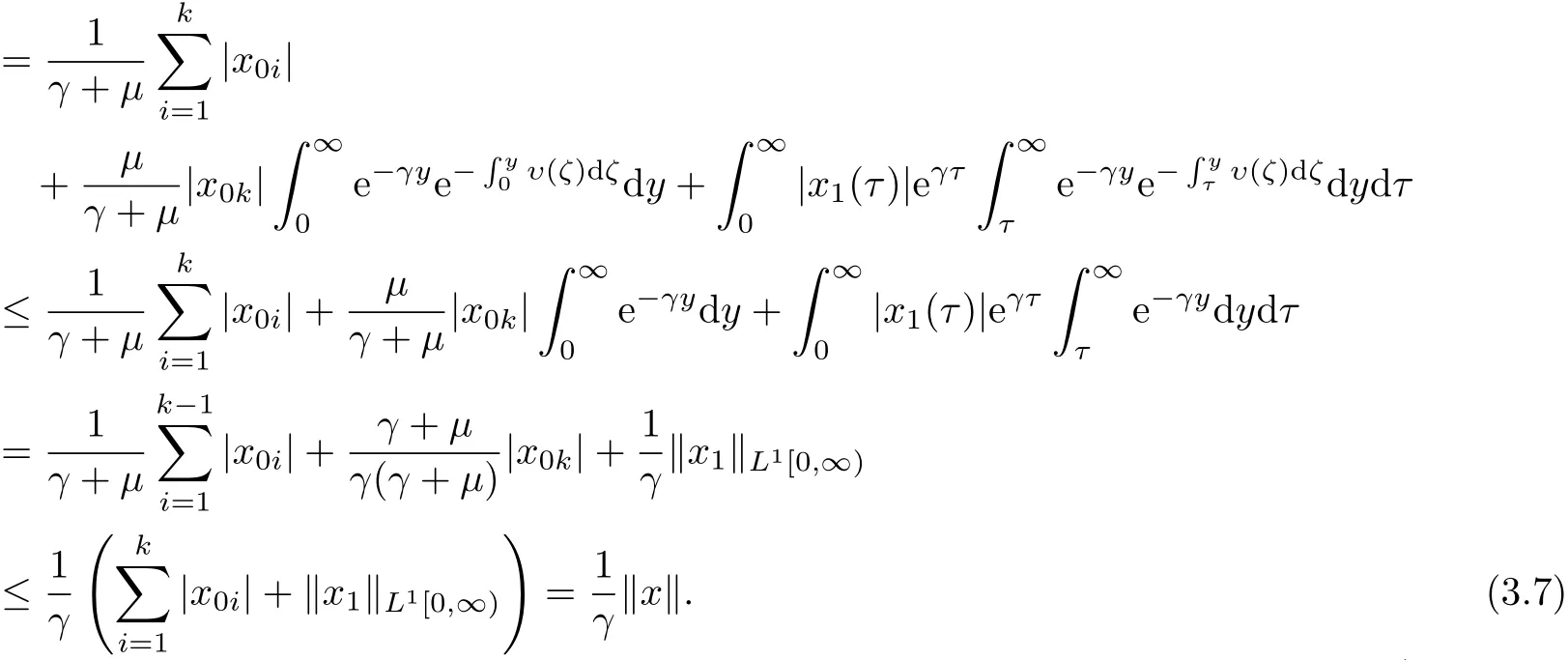
(3.7)说明当γ ＞ 0时,(γI − A)−1存在且(γI − A)−1:X → D(A)满足第二步证明D(A)在X中稠密.若取使得∀y∈[0,c]有p1(y)=0},

则由文献[7]知L在X中稠定.于是只需验证D(A)在L中稠定即可.

任取p=(p01,···,p0k,p1(y))∈ L,则存在常数c＞ 0,使得y∈ [0,c]有p1(y)=0.定义

这里

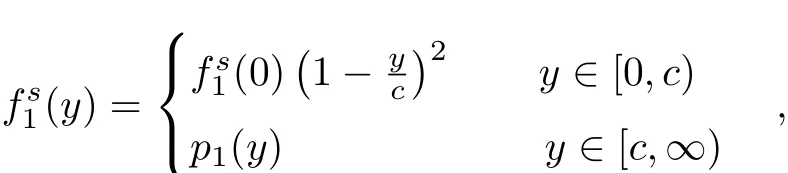
则易证fs∈D(A),还有

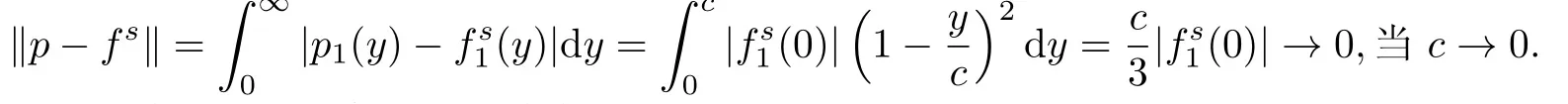
上式表明D(A)在L中稠定,即D(A)在X中稠定.从而由上面的两步与Hille-Yosida定理[8]得到A生成一个C0-半群.

第三步指出U和E是有界线性算子.对任意给定的p(y)∈X,由U和E的定义容易推出

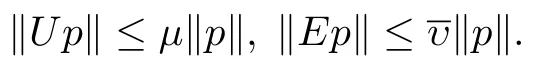
此外易见U和E是线性算子.因此结合C0-半群的扰动理论[8]得到A+U+E生成一个C0-半群T(t).

第四步证明A+U+E是dispersive算子.为此任取p(y)=(p01,···,p0k,p1(y))∈X并定义

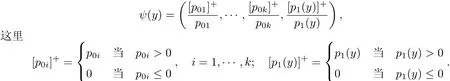
如果定义V={y∈[0,∞)|p1(y)＞0}和W={y∈[0,∞)|p1(y)≤0},则由文献[9]知道

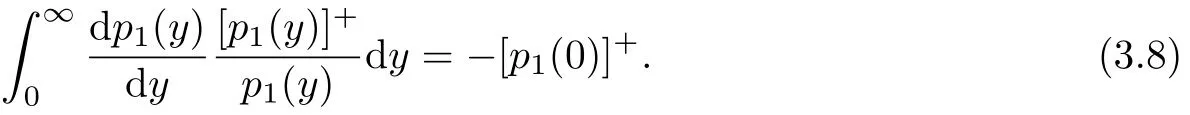
对任意的p∈D(A)和上述的ψ(y),用(3.8)式,边界条件与不等式2,···,k)得到

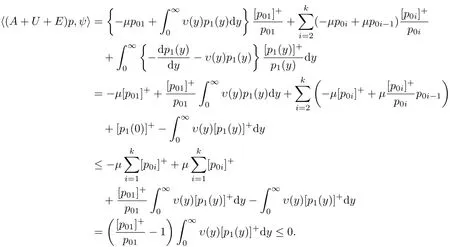
此式与dispersive算子的定义[10]知道A+U+E是dispersive算子.从而由第一步,第二步,第四步和Phillips定理得到A+U+E生成一个正压缩C0-半群.再由半群的唯一性理论即知,这个正定压缩C0-半群就是T(t).

类似于定理3.1的推导过程易得下面结果：

推论3.1A+U生成一个正压缩C0-半群Q(t).

由文献[11],不{难求出X 的共轭空间?X∗为{}}

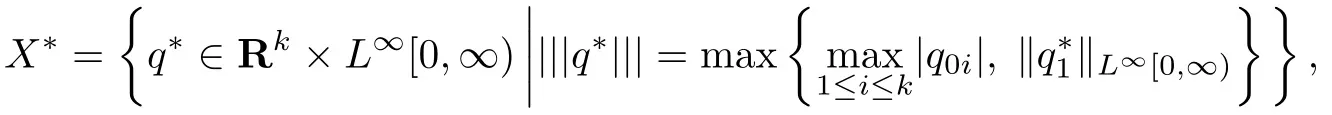
易证X∗是一个Banach空间[6].在X中引进集合

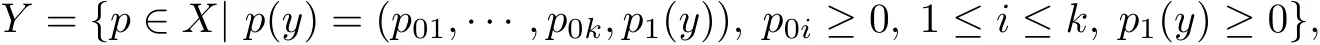
则引进的集合Y是X中的锥.对任意的p∈ D(A)∩Y,取q∗= ‖p‖(1,1,···,1),那么q∗∈ X∗,同时有

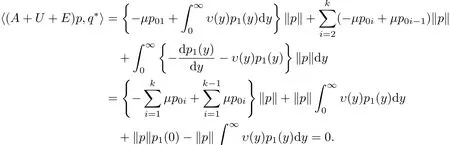
上式说明算子A+U+E对集合

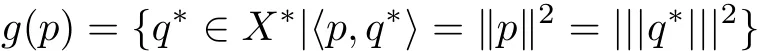
是保守算子.由于p(0)∈D(A2)∩Y,因此运用Fattorini定理[12]得到如下结论：

定理3.2T(t)对于系统(2.6)的初值p(0)是等距算子,即

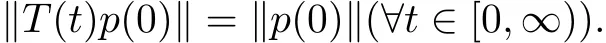
由本节的以上两个定理得到本节的主要结果，即

定理3.3则系统(2.6)具有唯一的正时间依赖解p(t,y),满足

证由定理3.1与文献[13]中的定理11知道系统(2.6)存在唯一的,非负的时间依赖解

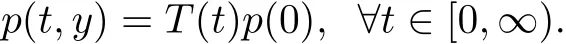
上式合并到定理3.2推出

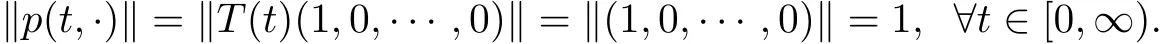
上述定理恰好反映了假设1的合理性和p(t,y)的实际背景.

§4 系统(2.6)相应算子的谱的特征

引理4.10是A+U+E的几何重数为1的特征值.

证讨论方程(A+U+E)p=0,即

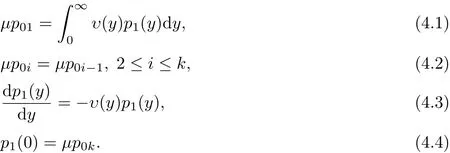
解(4.2)与(4.3)并利用边界条件(4.4)有

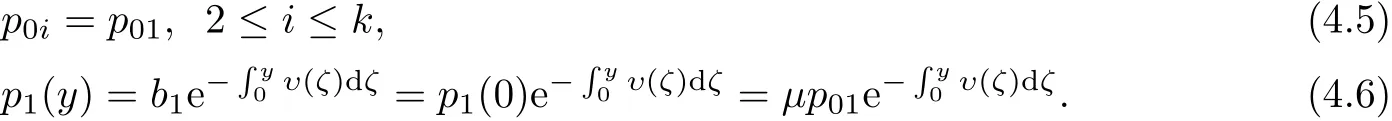
由(4.5)与(4.6)估计出

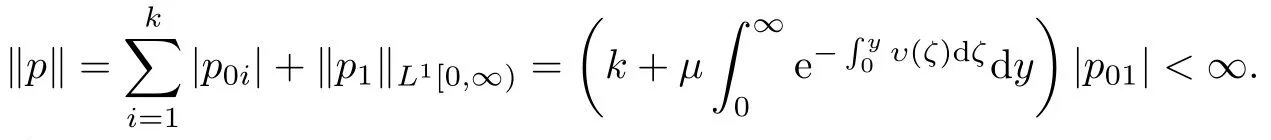
此式表明0是A+U+E的的特征值.同时由(4.5)与(4.6)知道对应于0的特征向量空间是1维的线性空间.即0的几何重数为1.

下面研究A+U+E的豫解集.首先定义极大算子(Am,D(Am))来定义算子(A0,D(A0))并研究它的豫解集.其次通过考虑(γI−Am)的核来定义Dirichlet算子Dγ并结合到边界算子Φ的定义推出ΦDγ的表达式.接着用文献[14]中的结果得到A+U+E的豫解集,并结合到得到的其它结论推出本文的主要结果.

首先定义极大算子Am和它的定义域D(Am)为[5]是绝对连续函数}.

选取X 的边界空间∂X:=C,并且定义边界算子L:D(Am)→∂X与Φ:D(Am)→∂X如下：

如果定义算子((A+U+E),D(A+U+E))为

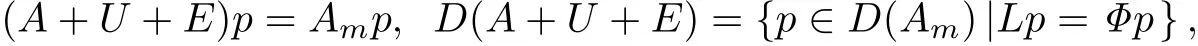
那么方程(2.1)-(2.5)可以描述为像(2.6)一样的的抽象Cauchy问题.

由极大算子(Am,D(Am))来定义算子(A0,D(A0))为

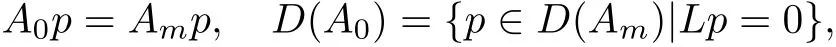
由上述表达式和豫解式的定义可得以下结论：

引理4.2设υ(y):[0,∞)→[0,∞)是可测函数,若

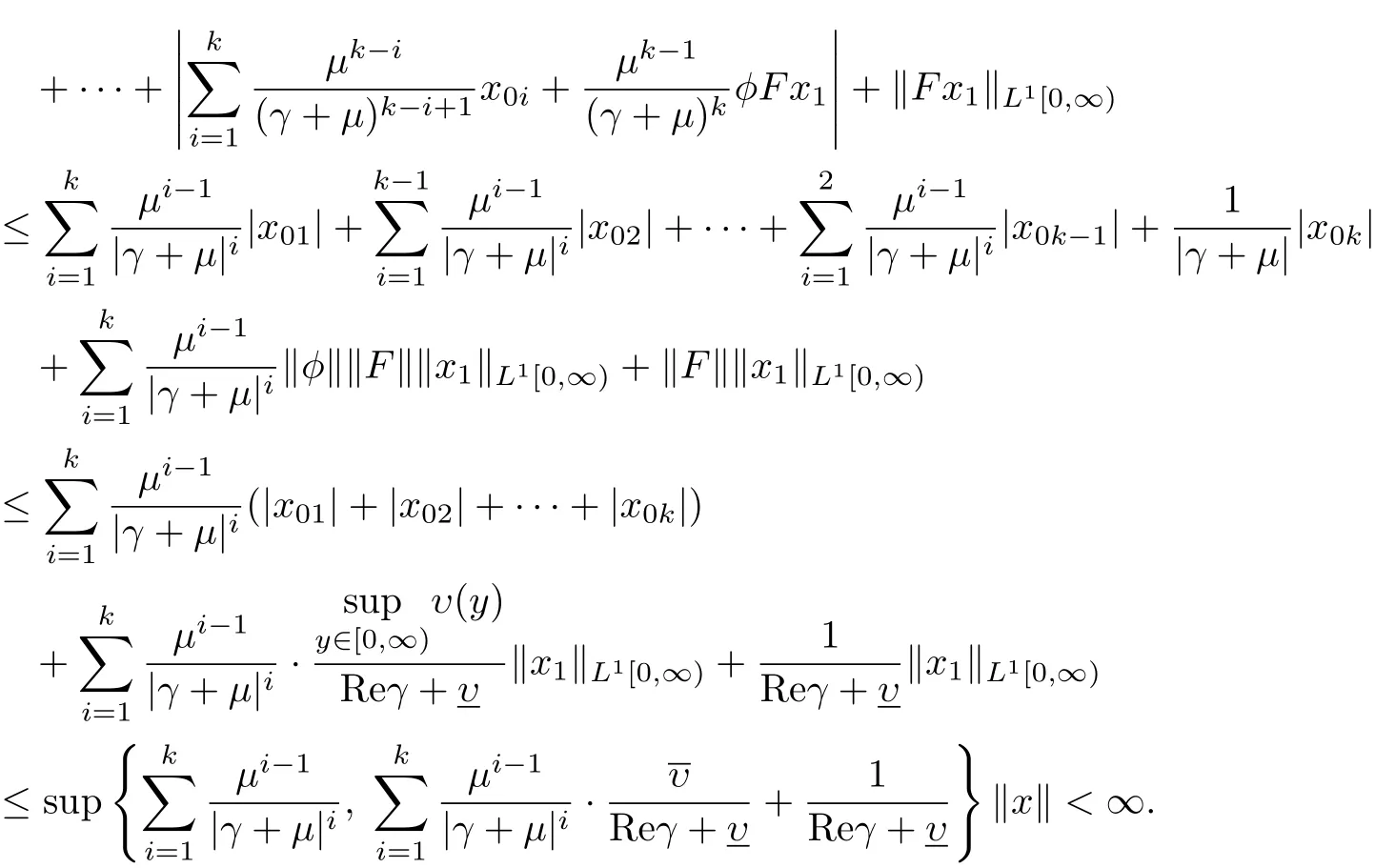
此式说明引理的结论成立.

引理4.3设υ(y)是可测函数,且

反之,若式子(4.18)与(4.1∫9)成立,则有

(4.27)与(4.28)说明p ∈ ker(γI − Am).

由于L是满射,所以

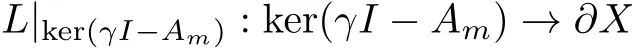
可逆.如果γ∈ρ(A0),那么定义Dirichlet算子为

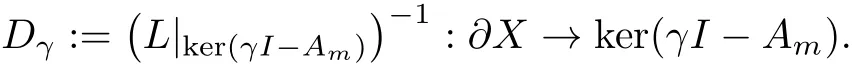
由引理4.3知道算子Dγ的具体表达式为

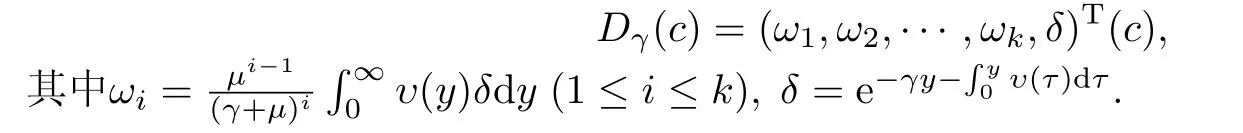
由Dγ的表达式和Φ的定义得到的具体表达式：

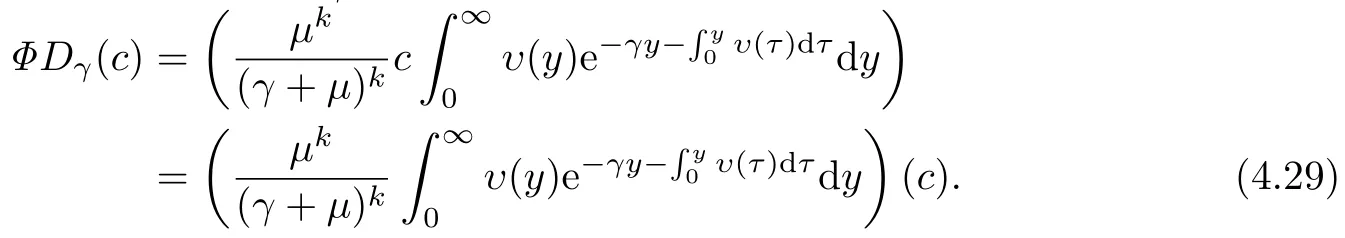
在文献[14]中作者得到如下结论：

引理4.4设γ ∈ ρ(A0)且存在γ0∈ C使得1/∈ σ(ΦDγ0),则

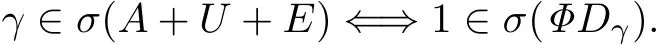
结合引理4.4与文献[10]得到如下结论：

引理4.5设υ(y)是可测函数,若

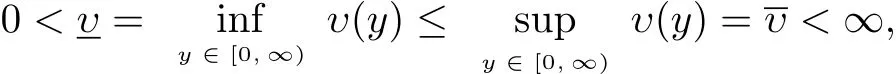
那么在虚轴上除了0外其它所有点都属于A+U+E的豫解集.

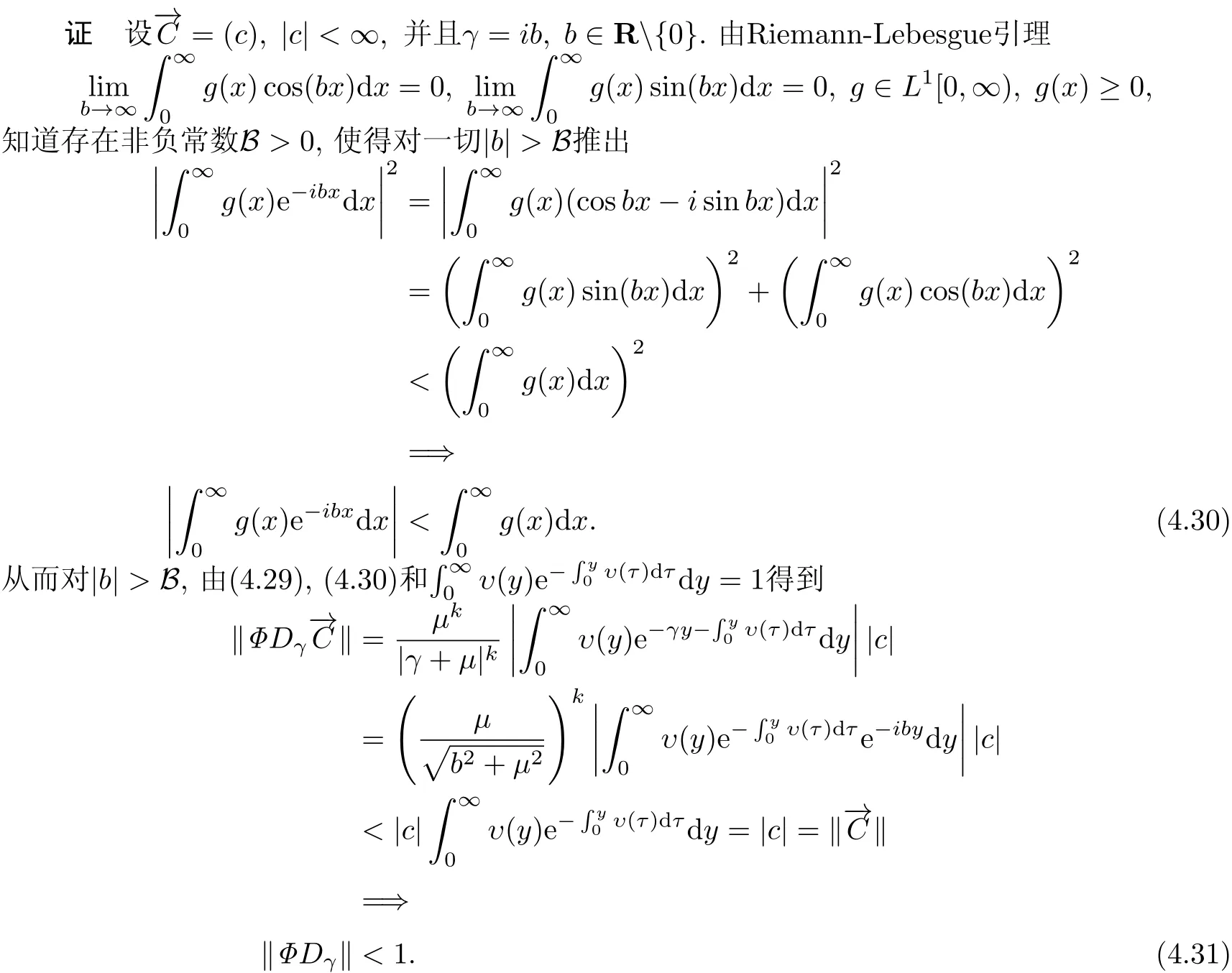
(4.31)说明当|b|＞ B时谱半径r(ΦDγ)＜ ‖ΦDγ‖ ＜ 1,这表明1/∈ σ(ΦDγ).此结果结合引理4.4知道当|b|＞ B时有γ /∈ σ(A+U+E),即

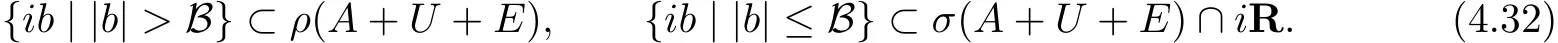
另外由定理3.1与文献[10]中的推论2.3知道σ(A+U+E)∩iR是虚加法循环.即

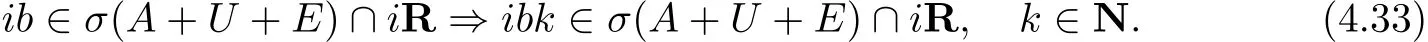
从而由(4.32),(4.33)与引理4.1推出σ(A+U+E)∩iR={0}.

引理4.6A+U+E的共轭算子(A+U+E)∗为

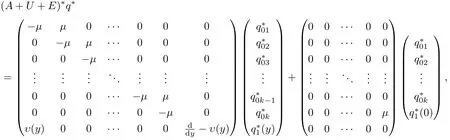
(4.34)及共轭算子的定义知道引理的结论成立.

引理4.70是(A+U+E)∗的几何重数为1的特征值.

证考虑方程(A+U+E)∗q∗=0,即

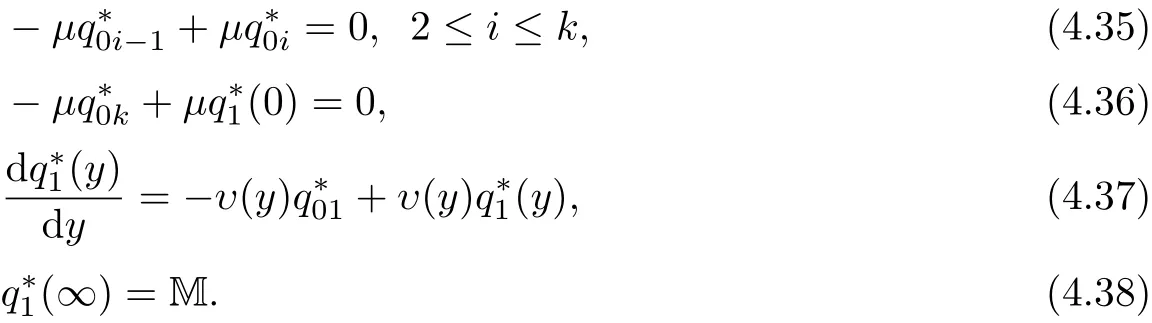
解(4.35)与(4.36)推出

§5 系统(2.6)时间依赖解的渐近行为

由于定理3.1,引理4.1,引理4.5,引理4.7恰好是文献[13]中的定理14的条件,因此这些结论结合到文献[13]中的定理14推出本文的主要结论：

定理5.1设υ(y)是可测函数,且满足

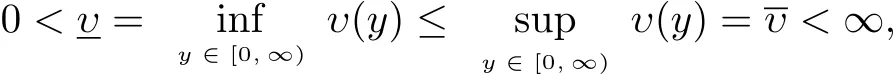
则系统(2.6)的时间依赖解强收敛于该系统的稳态解,即

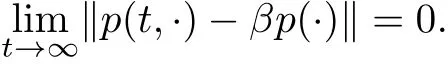
其中p(y)是引理4.1中的特征向量.

定理5.1说明假设2成立.

参考文献:

[1] 曹晋华,程侃.服务台可修的M/G/1排队系统分析[J].应用数学学报,1982,5(2):113-127.

[2] 朱翼隽.一个数据传送装置可修的计算机系统的性能分析和最优经济策略[J].数理统计与应用概率,1992,7(3):296-304.

[3] 曹晋华.服务设备可修的机器服务模型分析[J].数学研究与评论,1985,5(4):89-96.

[4] 朱翼隽.寿命为爱尔兰分布的可修闭路排队系统分析[J].江苏理工大学学报,1997,18(1):99-106.

[5] Greiner G.Perturbing the boundary conditions of a generator[J].Houston Journal of Mathematics,1987,13(2):213–229.

[6] 阿力木·米吉提,蔡玲霞.第二种服务可选的M/M/1排队模型状态空间及对偶空间的完备性[J].新疆师范大学学报(自然科学版),2012,31(2):72-76.

[7] Adams R A.Sobolev Space[M].New York:Academic Press,1975.

[8] Pazy A.Semigroups of Linear Operators and Applications to Partial Di ff erential Equations[M].New York:Springer-Verlag,1983.

[9] 阿力木·米吉提.带负顾客的非空竭服务休假排队模型非负解的存在唯一性[J].江西师范大学学报(自然科学版),2014,38(6):574-577.

[10]Nagel R.One-Parameter Semigroups of Positive Operators[M].Berlin:Springer-Verlag,1987.

[11] 定光桂.巴拿赫空间引论(第二版)[M].北京:科学出版,2008.

[12]Fattorini H O.The Cauchy Problem[M].Massachustes:Addison-Wesley,1983.

[13]Gupur G,Li X Z,Zhu G T.Functional Analysis Method in Queueing Theory[M].Hertfordshire:Research Information Ltd.,2001.

[14]Haji A,Radl A.A semigroup approach to queueing systems[J].Semigroup Forum,2007,75(3):609–623.

Asymptotic property of the time-dependent solution of the repairable closed queueing model with server of Erlangian distributed life time

Alim Mijit
(School of Distance Education,Xinjiang Radio&TV Univ.,Urumqi 830049,China)

By using the C0-semigroup theory,this paper studies the repairable closed queueing system with server of Erlangian distributed life time.First,by using the Hille-Yosida theorem,Phillips theorem and Fattorini theorem in functional analysis,the existence and uniqueness of nonnegative time dependent solution of system model has been proved.Next,the spectral properties of the operator corresponding to system model are investigated,which show that all points on the imaginary axis except zero belong to the resolvent set of the operator and zero is an eigenvalue of the operator and its adjoint operator with geometric multiplicity one.Thus,the above results give that the time-dependent solution of the system model converges strongly to its steady state solution.

C0-semigroup;dispersive operator;eigenvalue;resolvent set;geometric multiplicity

47D03;47A10

O177.92;O177.7

A

:1000-4424(2016)03-0281-13

2016-03-17

2016-04-16

新疆少数民族科技人才特殊培养计划科研项目(2016D0211)