一道习题的思考

安徽省颍上县第一中学　　程晓烨　　(邮编：236200)



一道习题的思考

安徽省颍上县第一中学程晓烨(邮编：236200)

在数学教学中，立体几何部分往往成为学生学习的难点.在立体几何中,经常通过平面几何的相关知识、方法来解决有关问题.下面以一道习题来探究平面几何和立体几何之间的联系：

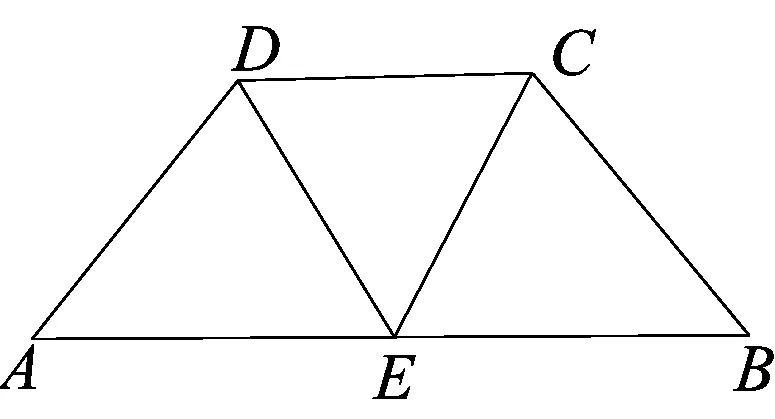
图1

1问题的提出

如图1,在等腰梯形ABCD中,AB=2DC=2a,∠DAB=600,E是AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B点重合,求形成的三棱锥的内切球和外接球的体积.

2问题的解决

分析由已知条件知,平面图形中,AE=EB=BC=CD=DA=DE=EC=a，所以折叠后得到一个正四面体.

我们先来思考：在平面中,若正三角形ABC边长为a,如何求它的内切圆和外接圆面积呢?

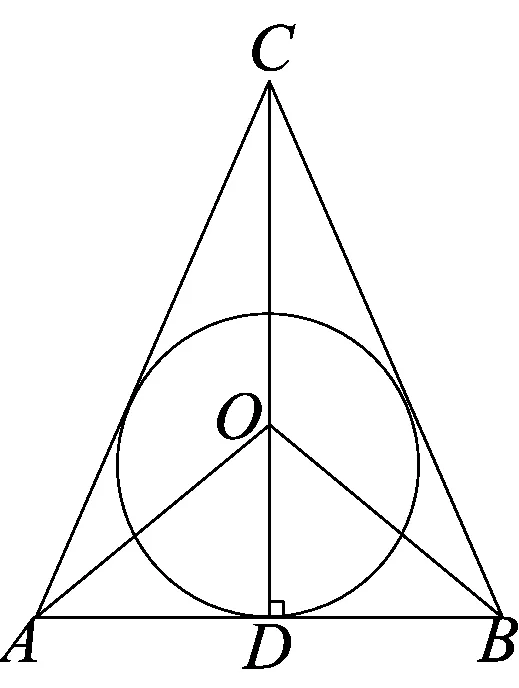
图2

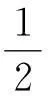
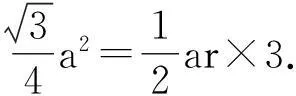
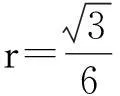
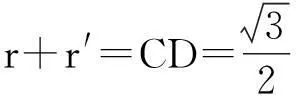
在正三角形中,我们可以通过等面积法求出其内切圆半径,再根据其内切圆半径和外接圆半径之和等于正三角形的高,求出其外接圆半径.那么推广到正四面体能不能用类似的方法解决其内切球半径和外接球半径问题呢?

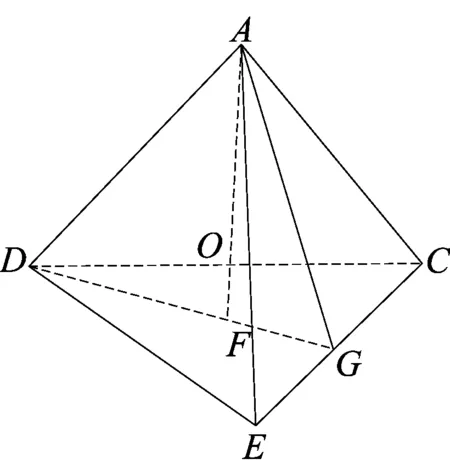
图3

例题中将等腰梯形如图折叠就可以得到棱长为a的正四面体,下面我们来求它的内切球半径和外接球半径.

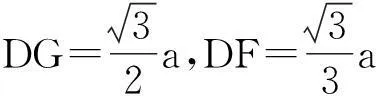
设正四面体内切球半径为R,球心O把正四面体分成四个三棱锥O-ADC、O-ADE、O-AEC、O-DEC,它们体积相等,均等于

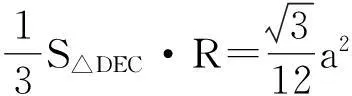
由等体积法得正四面体A-DEC体积等于四个三棱锥体积之和.即

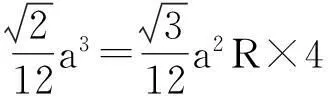
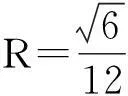
3问题的再思考

接下来再来求其外接球半径R′.

解法1正四面体内切球球心与外接球球心重合,内切球半径和外接球半径之和等于正四面体的高.

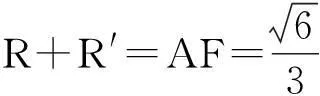
总结正三角形内切圆的圆心与外接圆的圆心重合,半径之比为1∶2,面积之比为1∶4,正四面体内切球的球心与外接球的球心重合,半径之比为1∶3,体积之比为1∶8.

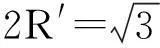
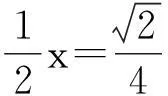
由正三角形的内切圆、外接圆半径的求法推广到正四面体内切球、外接球半径的求法,让学生体会平面几何和立体几何之间的联系,发现平面几何中的很多性质可以类比推广到立体几何中.立体几何在考查学生观察能力、思维能力和空间想象能力方面有重要作用,而由平面几何的知识、方法入手去分析不失为一种好的解题思路.

参考文献

1弼盛.同步导学案.济南：济南出版社,2008

2李凤华.正四面体外接球和内切球半径的求法.中学数学杂志,2008(1)

(收稿日期：2016-03-12)