2016年安徽省数学学科调研性试题分析与备考建议

安徽省教育科学研究院　　李院德　　(邮编：230001)



复习

2016年安徽省数学学科调研性试题分析与备考建议

安徽省教育科学研究院李院德(邮编：230001)

摘要为了加强对高考使用全国卷背景下高中数学教学的指导，安徽省教科院组织学科专家研制了数学学科调研性测试题.根据测试情况，以及对具体试题的分析，就如何做好高三数学复习教学进行了若干思考，对备考工作提出一些建议.

关键词全国卷；调研试题；备考建议

2016年安徽省数学学科调研性试题分文、理科，各五道大题，分别是解答题第17题，第21题，以及选做题第22题，第23题和第24题，重点就数列、导数、选修4-1、4-4和4-5等内容进行了考查.

1试题的总体特点

此次安徽省数学调研性试题的命制，主要依据《2016年普通高等学校招生全国统一考试大纲》的要求，参照高考全国卷Ⅰ的命题风格，充分考虑“安徽卷”与“全国卷”考查重点的不同，特别关注我省普通高中数学教学的实际情况.

在题型与难度方面，试题兼顾了传承与创新的关系.在确保科学性与规范性的前提下，试题注重基础知识、基本方法、数学思想和数学能力的考查.通过测试学校反馈的情况看，学生在答题过程中出现的错误和问题具有一定的共性，反映了我省高考数学复习存在着一些不足，这表明调研性试题具有很好的测试和反馈功能，既让高三师生初步感知了“全国卷”的要求，又为下一步高考复习提升效益指引了方向.

2数据分析

2.1数据来源

为了确保数据的科学性、有效性和准确性，笔者随机选取了一所普通高中使用调研性试题进行了测试，从该校698名理科学生中随机抽取195人、262名文科学生中随机抽取122人，对他们的答题情况进行了分析.

2.2数据统计

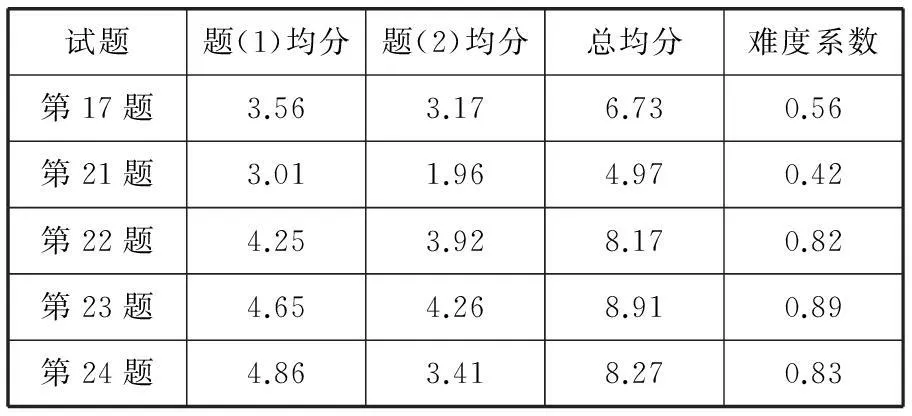
表1　理科测试情况

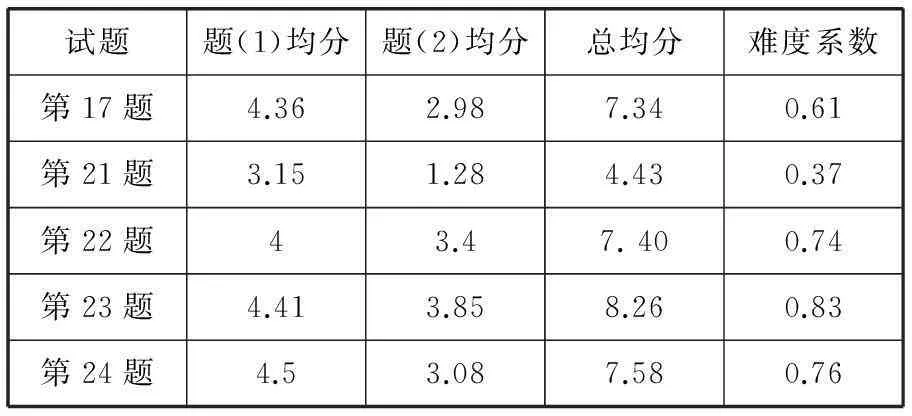
表2　文科测试情况

3试题分析

3.1对第17题的分析

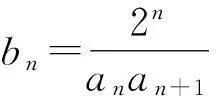
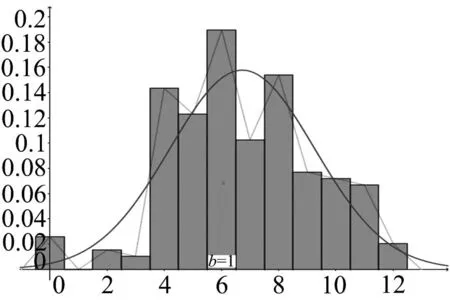
图1　理科第17题得分情况的频率分布直方图

试题分析第(Ⅰ)问可以通过函数的奇偶性确定零点，从而得到递推公式.根据递推公式可求通项公式.主要失分原因有：

(1)由于综合考查了函数与数列的相关知识，不少学生不会分析解决问题的途径；

(2)部分学生虽然得到了递推公式，却不会由递推公式求通项公式，或者在求解过程中运算错误；

(3)几乎没有同学考虑到求出通项公式后还需要进行检验，反映出了思维的严密性有待提高.

第(Ⅱ)问失分的主要原因是：部分学生没能发现新数列的特点(分子正好是分母中两项的差)，这也是正确解决问题的关键.

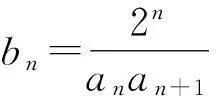
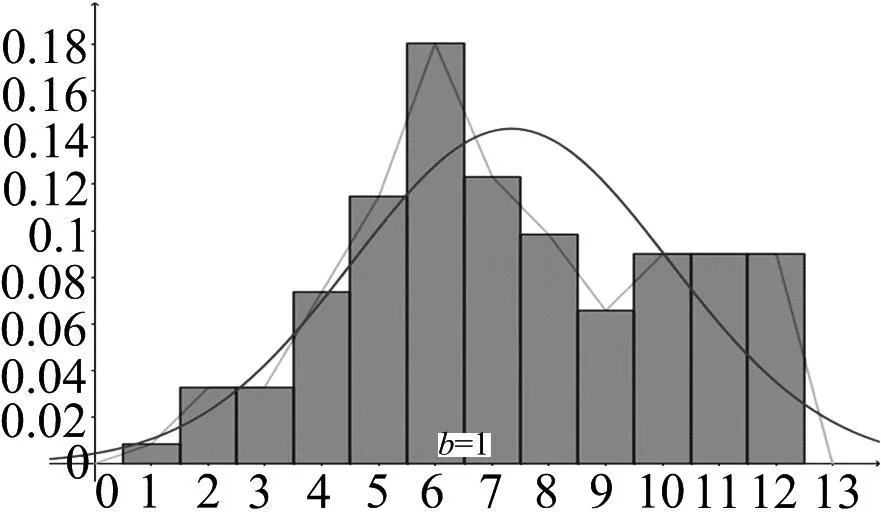
图2　文科第17题得分情况的频率分布直方图

试题分析第(Ⅰ)问根据

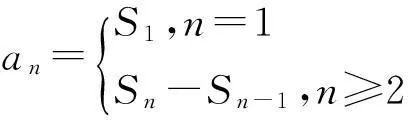
第(Ⅱ)问失分原因与理科相同.

复习建议从近五年高考全国Ⅰ卷看，理科2011、2014、2015和文科2011、2014年第(17)题均是数列题，主要考查了数列的定义、通项公式，以及特殊数列前n项和.建议二轮复习要夯实基础，重点让学生掌握好等差、等比数列的定义、性质，通项公式和前n项和公式.加强基本技能的训练，如利用递推公式求数列通项公式的常见方法，以及常用的求和方法(如错位相减法、裂项相消法、分组求和法等).同时，要注重培养学生的运算求解和推理论证的能力.

3.2对第21题的分析

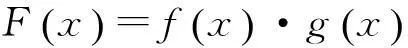
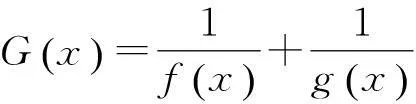
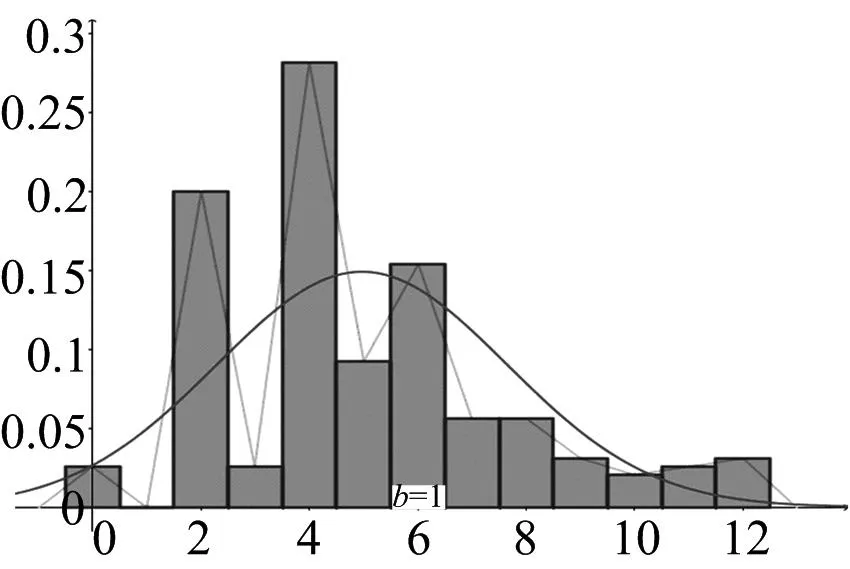
图3　理科第21题得分情况的频率分布直方图

试题分析第(Ⅰ)问对函数求导，问题转化为对含参方程在(0，+)内有根的讨论.暴露的问题有：(1)公式不熟，求导错误；(2)分类讨论时出现错误；(3)仅仅说明函数单调区间，没有指出极值点.

第(Ⅱ)问可以说是调研性试题的压轴一小问.许多学生对其敬而远之，主要原因是学生思维的抽象能力不强，理性思维深度不够，难以发现问题的本质.另外，也与时间不够和畏难情绪有关.

文科第21题已知函数f(x)=xlnx+ax2.

(Ⅰ)若f(x)在定义域内为单调递减函数，求实数a的取值范围；

(Ⅱ)若函数f(x)有两个零点x1、x2,证明：x1·x2>e2.

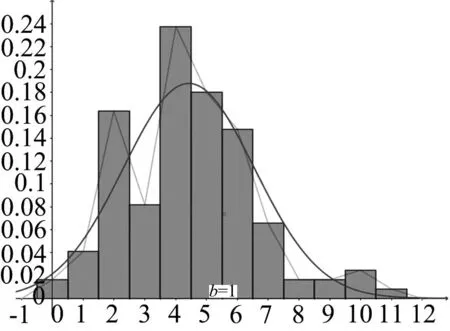
图4　文科第21题得分情况的频率分布直方图

试题分析第(Ⅰ)问利用导函数来研究函数的单调性，从而求出实数a的取值范围，是常见的恒成立问题，采用分离变量构造新函数很容易求出正确结果.需要注意的是，一定要在定义域内讨论.主要失分原因有：(1)求导出现错误；(2)思维的灵活性不够，没有想到用分离常数的办法.

第(Ⅱ)问对欲证不等式作等价变形，再构造函数解决问题.第(Ⅱ)问要求学生能够灵活运用所学的知识，对学生的创新意识要求较高.与理科的情形相似，绝大多数的同学没有解答.

复习建议2011-2015年，全国Ⅰ卷导数试题(除2013年文科卷是第20题)所处的位置和难度非常稳定，综合性较强，对学生的数学素养提出了较高的要求.建议在复习中要做好以下几点：

(1)重视导数在研究函数中的突出地位.不仅要让学生了解导数的概念和背景，更重要的是要让学生掌握利用导数的基本知识解决问题(如图象、单调性、最值、恒成立等问题以及函数的零点) 的一般方法，体会导数的通法作用.

(2)加强运用，培养学生利用导数解决问题的能力.如高考中经常出现的切线问题、含参问题、不等式问题、恒成立等问题.同时注重渗透数形结合、分类讨论、化归转化等思想，着重提升学生的抽象概括、推理论证、运算求解能力，以及应用意识和创新意识(尤其是构造函数的能力).

3.3选做题分析

对于“三选一”(第22、23和24题)的选做题，绝大多数学生选择了第23题，反映了学生整体对选修4—4专题掌握较好，也反映出一些学校对选修部分教学存在着一定的偏好，与使用全国卷的有关省份高考选做题情况基本吻合.

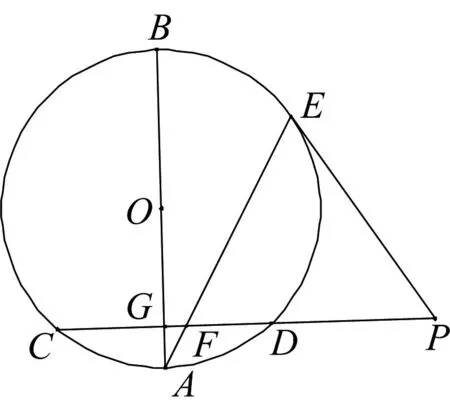
第22题(选修4-1：几何证明选讲)如图，AB是圆O的一条直径，弦CD垂直于AB,垂足为点G,E是劣弧BD上一点，点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.

(Ⅰ)求证：PE=PF；

(Ⅱ)求证：DF·CF=2GF·PF.

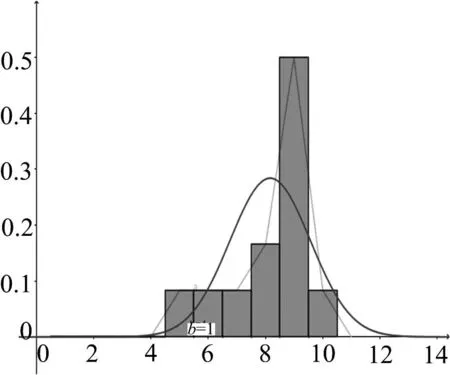
图6　第22题理科学生得分情况的频率分布直方图

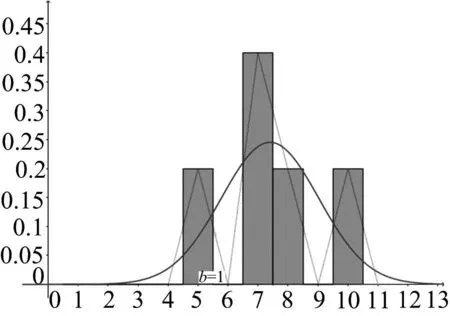
图7　第22题文科学生得分情况的频率分布直方图

试题分析整体来说，这道题得分率比较高.出现的问题主要是：基本定理不太熟悉，不会构造辅助线，或者是对几何证明有畏难情绪.对于几何证明选讲专题的考查，全国Ⅰ卷近五年来主要考查了四点共圆的判定和性质、射影定理、相交弦定理、弦切角、三角形相似的性质与判定等内容，主要是考查学生的几何思维与逻辑推理能力，考查学生的几何直观与空间观念.

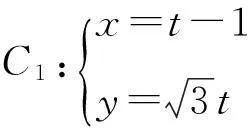
(Ⅰ)求曲线C1与曲线C3交点的直角坐标；

(Ⅱ)若P是曲线C2上的动点，Q是曲线C3上的动点，求|PQ|的最小值.

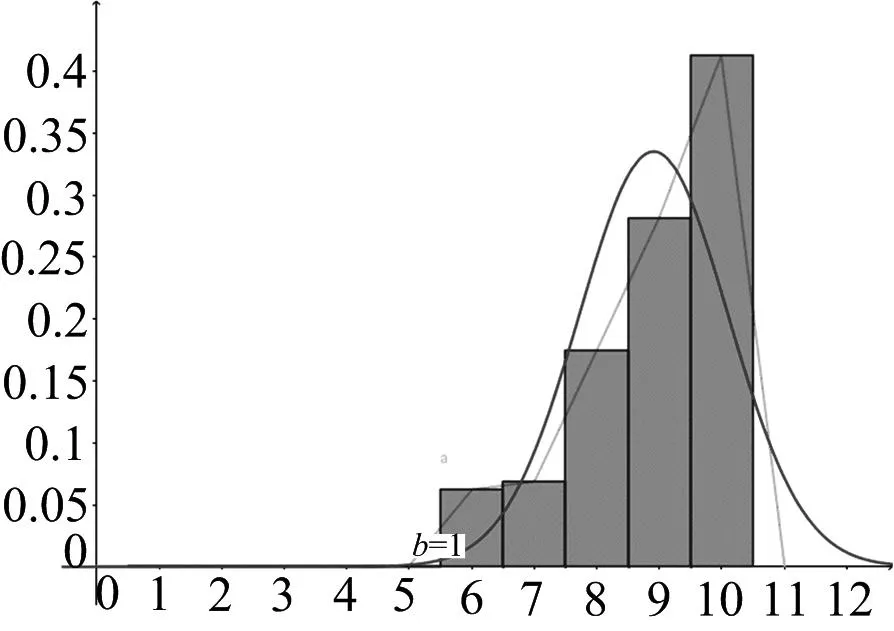
图8　第23题理科学生得分情况的频率分布直方图

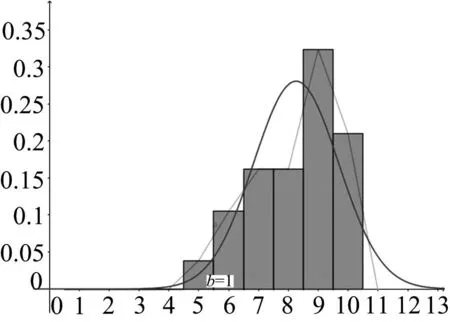
图9　第23题文科学生得分情况的频率分布直方图

试题分析本题考查直线的参数方程、圆的极坐标方程与直角坐标方程的互化，求直线与圆的交点坐标，利用点到直线的距离求最值问题，考查转化化归和数形结合思想.主要失分原因有：

第(Ⅰ)问部分同学可能是审题不清，漏看了还要求两条曲线的交点坐标，导致失分；

第(Ⅱ)问部分同学说理不清，仅有数学符号没有必要的文字加以说明.

近五年来，全国Ⅰ卷对于极坐标与参数方程，主要考查直角坐标方程、参数方程，与极坐标方程的相互转化，轨迹的参数方程，两点间的距离公式等问题，目的是为了让学生掌握曲线的参数方程与极坐标，以及它们之间的相互联系，有利于学生未来的学习与发展，难度适中.

(Ⅰ)试比较f(-1)与f(a)的大小；

(Ⅱ)若函数f(x)的图象和x轴围成一个三角形，求实数a的取值范围.

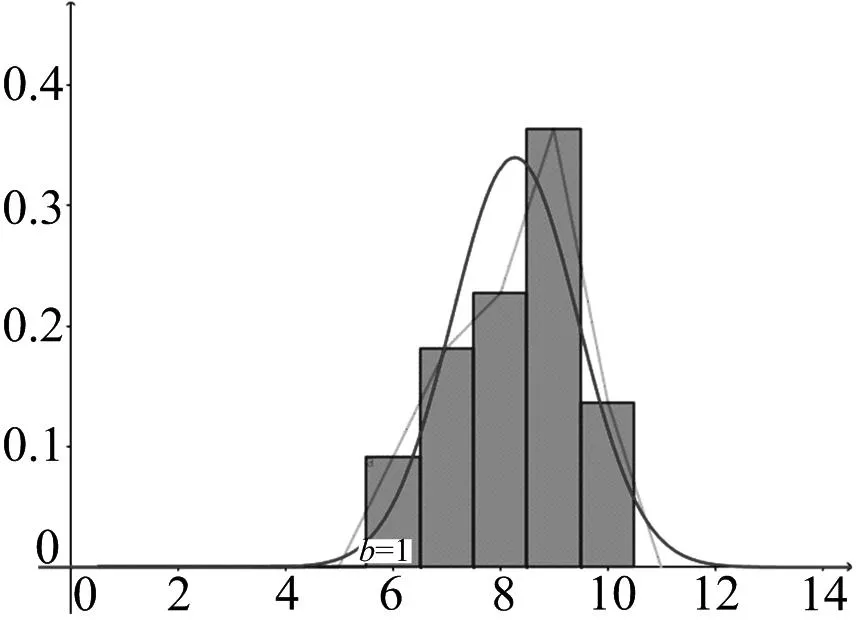
图10　第24题理科学生得分情况的频率分布直方图

试题分析本题考查含绝对值的函数值的大小比较，绝对值函数图象的特征等基础知识，以及分类讨论思想和运算求解能力.

第(Ⅰ)问比较大小可以考虑作差法，有的同学说理不清楚，直接说是显然的，而没有进行作差说明.

第(Ⅱ)问对函数图象和x轴围成一个三角形作等价转化，从而求出a的取值范围.有的同学分类不清楚，无法找到合适的方法.

近五年来，对于不等式选讲，全国Ⅰ卷在2011年、2012年、2013年2015年均考查了含有参数的绝对值不等式，2014年考查了均值不等式，涉及分类讨论、数形结合、转化化归思想等，难度适中.

复习建议(1)根据学生情况，凸显选修特色.对于选修内容，教师可根据学生的学习状况，既可以选择集中教学，也可以结合学生的学习水平分层教学.教学中应突出“选修”的特色，赋予学生“选”的权利，尊重他们的兴趣选择.在复习时段上可以和必修内容复习相结合，适当把选修内容穿插在必修内容之间， 同时复习过程中要根据复习内容、学生反馈的情况灵活调整，适当处理.

(2)丰富教学形式，重视探究性学习.选修部分内容不多，专题感强，有很好的探究价值.教师在教学和复习中可以分成多个小组，做一些探究性学习活动.

(3)重视考题特点，加强有效训练.教师要注重高考真题的研究价值和指导意义，可以对历年的真题进行测验、讲解.在此过程中，要根据学生情况和高考要求，避免过多过难过偏，防止增加学生的学习负担.

4对高三教学的几点思考

4.1夯实基础，构建良好的认知结构

以《考试大纲》为引领，重视对基本知识、基本技能和基本数学方法的教学，充分发挥教材在高考复习备考中的作用，帮助学生准确理解数学知识，了解知识间的逻辑关系和内在联系，建构完整、有序的知识网络，注重从知识整体的高度理解数学知识的本质，形成良好的认知结构.

4.2加强高考研究，把握备考方向

安徽卷与全国卷在试题风格、考查范围、试卷结构、知识点分布、考查侧重点以及能力要求上有一定的差异(可参考安徽省教育厅关于印发《2015-2016年度高三语文等九个学科教学指导意见》)，但安徽省高考试卷自主命题的指导思想与全国卷保持一致，命题始终遵循《考试大纲》，着重考查学生分析问题和解决问题的能力，这个本质是不变的.因此，我们要认真研读《考试大纲》，不仅要重视把握知识考查的范围与要求，更要重视对能力的要求，只有这样，才能使培养学生的能力落到实处.另外，我们还要研究全国卷的真题，重视解题方法和策略的研究，要善于帮助学生在解题过程中总结解题方法，积累解题经验.

4.3突出数学思想，注重提升能力

主要做好两个方面的工作：一要重视数学思想方法的复习与应用.到了复习阶段，教师应该对数学基本思想、方法进行梳理、总结，逐个认清它们的本质特征和相互联系，自觉、灵活地应用于所要解决的问题中；二要重视思维能力的培养.复习教学要在重视基础知识掌握的同时，更加注重学生数学思维能力的提升.空间想象、抽象概括、推理论证等思维能力的培养应渗透日常教学和复习备考的全过程，要让学生在参与数学知识的形成、发展、应用和解题过程中，感悟数学思想方法.要注意挖掘例题所蕴含的内在的教学价值，重视一题多解、一题多变、多题一解，提升学生的数学能力和数学素养．

(收稿日期：2016-02-18)

考试