使学生在数学学习的“巧练”中实现增效减负
2016-07-08安徽省合肥市包河区教研室汪洪潮邮编230001
安徽省合肥市包河区教研室 汪洪潮 (邮编:230001)
教学
使学生在数学学习的“巧练”中实现增效减负
安徽省合肥市包河区教研室汪洪潮(邮编:230001)
摘要“减负增效“是一项艰巨的任务,减轻学生过重的课业负担是教师的职责之一.“减负”了不一定能“增效”,要实现“增效”的目的,教师在作业的设计时需要精雕细琢.“巧练”是指用尽可能少的作业量,实现尽可能高的“效率”.“巧练”要围绕核心知识和基本思想方法,抓住问题的本质和解决问题的方法,关注数学思维和能力的提升,促进学生数学素养的提升.
关键词减负增效;巧练;核心知识;数学能力;数学素养
自新课改以来,“减负增效”就一直是热门话题,从中央到地方、从教师到学生都在喊“减负”.可是,现实效果却不容乐观,学生“负担”不减反增,苦不堪言.曾有一次听到一位优秀的毕业班同学讲述:“我度过了终身难忘的一个寒假,每天坚持做老师布置的寒假作业达9小时,明天开学了,还没做完”.她的话让我心头一震,“减负”真的是“理想很丰满,现实很骨感吗”?问题到底出现在哪里?我们的学生为什么会有那么多写不完的作业?仔细一想,就会明白:“减负”是很好的倡议,但是作业少了,负担轻了,怎样保证考试成绩呢?怎样保证升学率呢?如果“减负”不能“增效”,谁还敢大胆“减负”?其实,如果“减负”单单是减量,效果肯定不行,要通过教学内部结构的变化、对教与学的重新认识、对教学方式的转变来减轻学生的负担,而要实现这一目标就必须先“增效”,才有可能实现“减负”.
合肥市中学数学教研室主持研究的课题《本真性数学课堂教学模式的实践研究》,旨在过“深备”、“先学”、“精导”、“巧练”等四个环节的研究,探索总结出“回归数学本真,打造高效课堂”的方法和经验.教师对课堂教学四个环节的有效实施,就是“提高效率”,只有教师先“增效”了,才有可能实现学生“减负”的目的,以下略谈如何使学生在数学学习中实施“巧练”达到增效减负的目的.
1“巧练”要立足主要知识和基本思想方法
“巧练”的重点是练,关键在于巧.一堂课的知识点可能很多,我们不能面面俱到,以“刷题”的方式眉毛胡子一把抓是不行的.应该根据教学目标,围绕课堂的主要知识和基本思想方法设计问题,使学生通过若干有效的问题训练,达到既巩固了主要知识,又领悟了思想方法,这样的练习才是“巧练”.如,在学习了《三角形中的边关系》后,设置如下问题就是比较合适:
案例1等腰三角形中,周长为18cm.(1)如果腰长是底边的2倍,求各边长;(2)如果一边长为4cm,求另两边长.
本题的解决首先要用到本节的“三角形两边之和大于第三边”的重点知识,其次又要用到“分类讨论”思想,最后,还要渗透方程的思想,可谓“一箭三雕”.难度不大,但内涵丰富,很有韵味,属高质量的问题.
相反,如果抓不住主要知识,纠结于细枝末节,设置大量有“陷阱”的问题,不仅会增加学生负担,反而对知识的学习与巩固不利.
案例2在学习二次函数定义后,为了巩固二次函数的概念,有老师布置了如下问题:
(1)如果函数y=(m-1)xm2+2m-2是二次函数,则m的值是______;
(2)如果函数y=(m-2)x|m+1|-1+(m+4)x+1是二次函数,则m的值是______.
这两题虽然巩固了二次函数概念中自变量指数为2,二次项系数不为0的要求,但解答过程却要用到解一元二次方程和绝对值方程等知识,既耗费时间,又不能有效巩固和检测主要知识,故不可取.
2“巧练”要突出知识的本质和解决问题的方法
同一节课知识点是有限的,但题目是无限的,如何引导学生从无边无际的题海中跳出来,需要老师抓住知识的本质和解决问题的方法,只有这样才能“既见树木又见森林”.
在一次《“一线三直角”模型的复习》课中,老师一方面收集关于“一线三直角”模型的有关中考题,让学生仿着做、学着练,又布置如下问题让学生解决,既没有分析“一线三直角”模型试题的特点、也没有对有关“一线三直角”模型题型的拓展,更没有对“一线三直角”模型的解题方法予以总结.
案例3如图1,B、E、C在同一直线上,且∠B=∠C=∠AED=90°.
求证:△ABE∽△ECD.
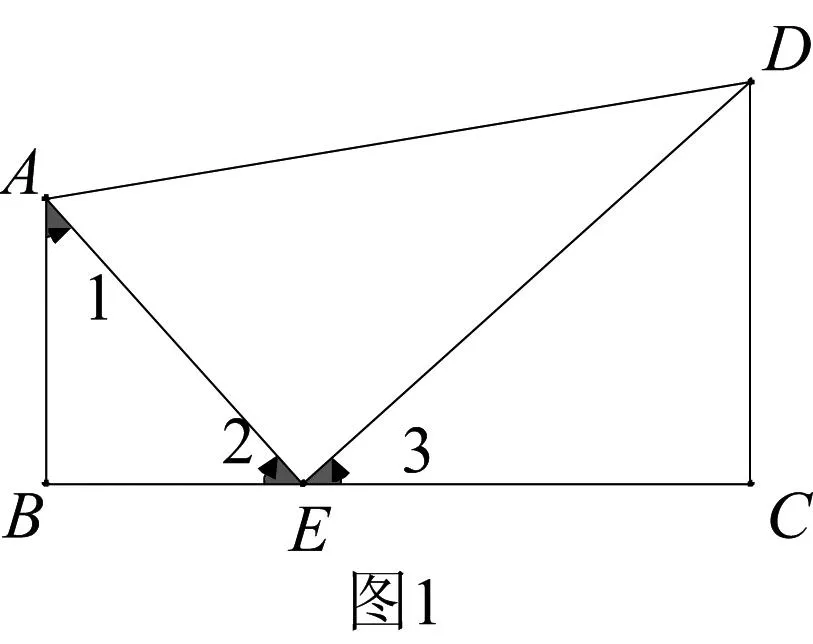
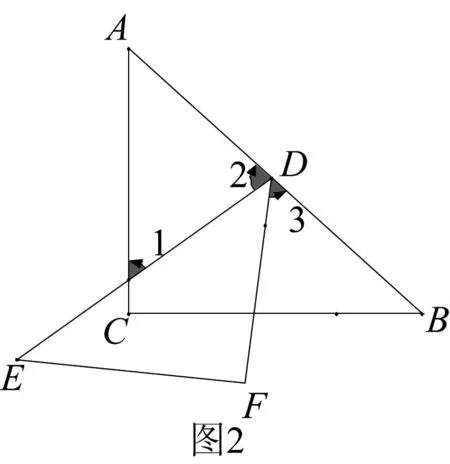
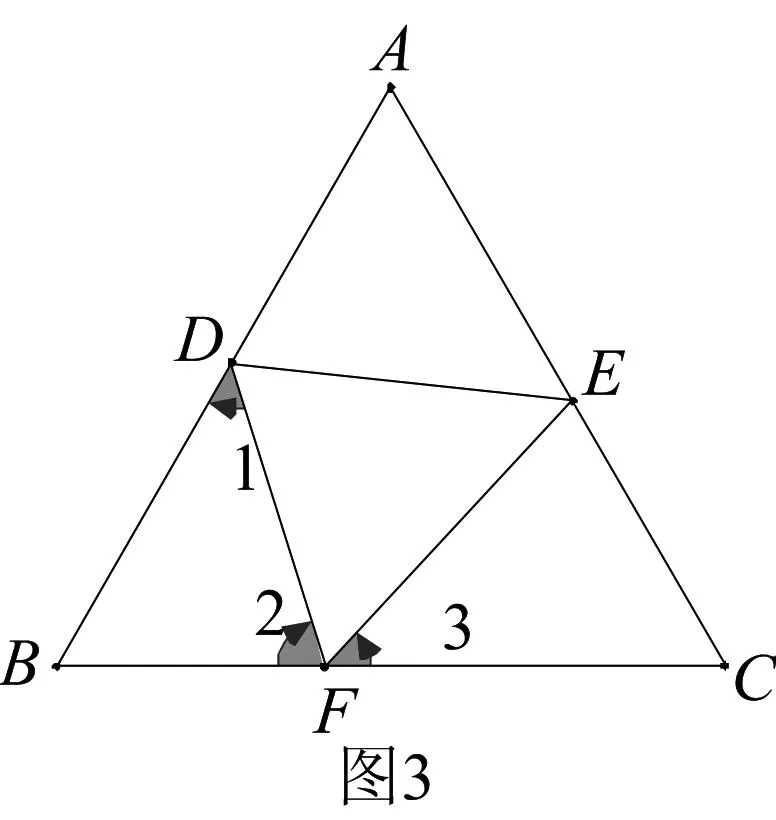
“一线三直角”是两三角形相似的常见模型,其关键是利用“∠1+∠2=90°和∠2+∠3=90°”得到“∠1=∠3”,但问题的本质远不止于此.如图2,将两个等腰直角三角形如图摆放,如图3,将等边三角形的一个角折叠,使顶点落在对边上,这两个图中都蕴含了两三角形相似,其本质和“一线三直角”类似,都是利用“∠1+∠2=180°-α”和“∠3+∠2=180°-α”来推出“∠1=∠3”的结论.
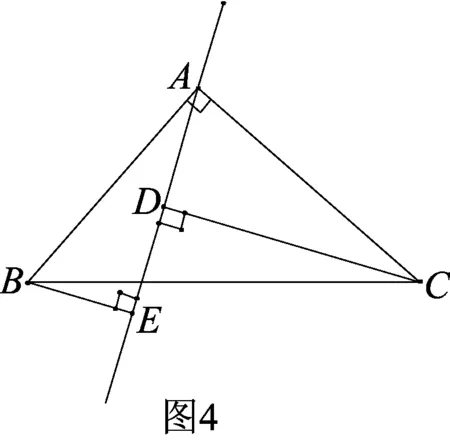
课堂复习不能就题讲题,应该抓住问题的本质,将“一线三直角”模型进一步变式和推广.
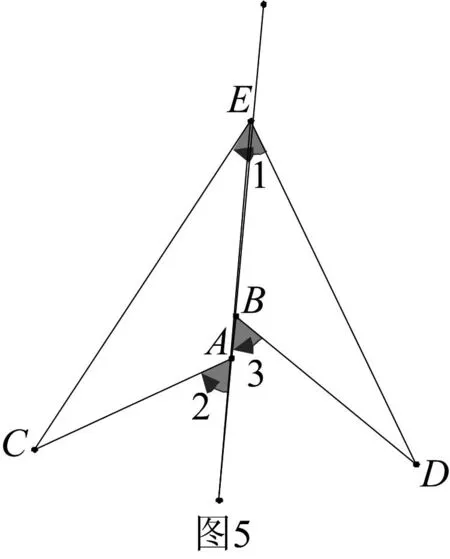
将这种模型进行如下变式,即等角在直线的两侧,如图4和图5,也可以得到相应性质.
如果将“一线三直角”模型运用到四边形中,可以发现类似的性质.
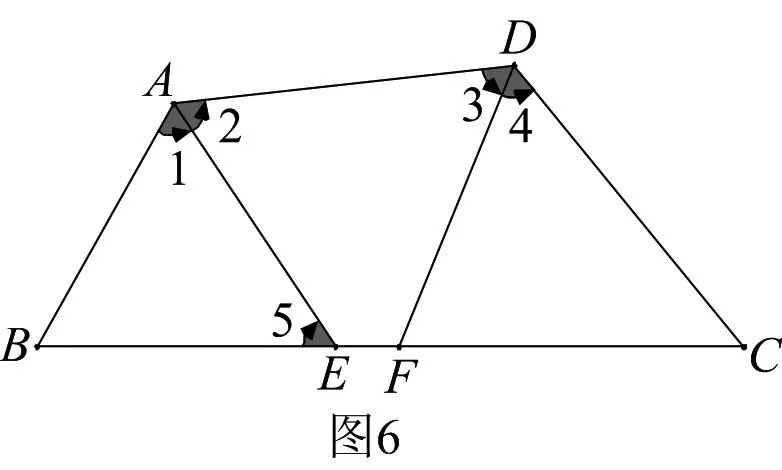
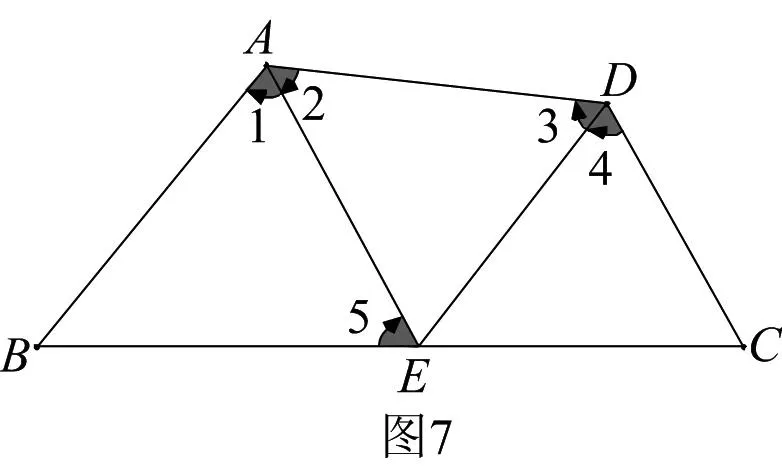
如图6,已知四边形ABCD中,∠B=∠C,AE、DF分别是∠BAD与∠CDA的角平分线,那么可以得到结论:△ABE∽△FCD.进一步,如图7,如果E、F重合,那么还可以得到结论:(1)△ABE∽△ECD∽△AED;(2)BE=CE;(3)BE2=AB×CD.
教师只有深刻理解和掌握了问题的内涵,才有可能引导学生掌握思考问题的方法,学会举一反三,触类旁通,达到解一道题而领悟解一类题的方法和思路.
3“巧练”要帮助学生将知识内化,促进能力的形成
课堂练习的目的是巩固知识,训练思维,形成技能.增效减负是要求设置集巩固知识、训练能力和掌握方法于一身的好问题,通过问题的训练,达到知识内化,形成技能的效果.如学习《线段、射线和直线》后,若安排如下问题:
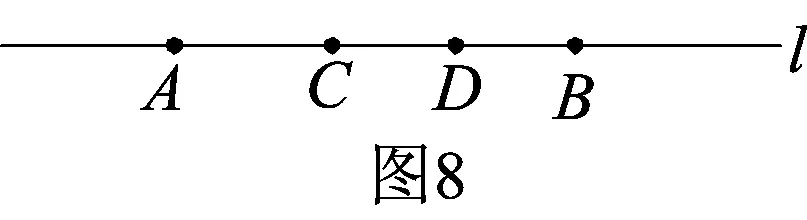
案例4 (1)如图8,直线l上依次有A、C、D、B四点,则图中线段共有几条?
(2)某次会议有5个人参加,如果每个人都和其他人握一次手,那么一个人要握几次手?一共握了多少次手?
问题(1)虽然简单,解决的方法也不同,但老师在分析时,总结了两种最基本的方法:其一是按线段上所含点的个数数,含有两个点的线段有AC、CD、DB三条,含有三个点的线段有AD、CB两条,含有四个点的线段有AB,总计共6条;其二是按线段的左端点依次数,左端点是点A的有AC、AD、AB三条,左端点是点C的有CD、CB两条,左端点是点D的有DB,共计六条.虽然方法不同,但结果都一样.重要的是,这样按一定顺序、有条理的“数法”,有助于学生发现所得结果的规律,进而推广到一般情况.把这样看似简单的问题讲清、讲透,为后续解决类似的“数角”、“数三角形”等问题提供经验,促进知识和方法的迁移,逐步发展成解决问题的技能.
问题(2)是参会人员握手次数的问题,老师将人抽象成平面内的点,将实际生活中的故事抽象成数学问题,将“握手问题”巧妙的转化为“数线段问题”,有效地将问题(1)中的“数线段”的思维方法应用于类似其他问题中,促进学生解决问题能力的提升.
在数学的学习过程中,往往有学生这样说,老师讲的都听得懂,自己做时就不会了.这种现象在几何证明中常常出现,比如一旦告诉了辅助线的添法,很多学生就会证明了.这种“不会添辅助线”的现象折射出学生没有真正学会思考、学会解题.南京师范大学涂荣豹教授在《解题教学与学习》的报告中指出,解题教学教师要“想给学生看”、“想给学生听”.要引导学生感悟“解法的自然”呈现.如下列问题:

案例5已知:如图9,△ABC中,D、E分别是边AB、AC上的点,且AD=AE,DE的延长线交BC延长线于点F,若BC∶CF=2∶3,求BD∶CE的值.
本题证明时,很多学生就是不知道如何添加辅助线,图中有很多点,从哪一点作平行线?为什么是这样?是如何想到的?为什么从点C作平行线比从点E做平行线好?这些问题都是需要认真考虑的.
其实,辅助线是沟通已知条件和求证结论的桥梁,教师在学生练习后要对此进行分析和总结,指出添加辅助线的规律,并安排一些与之相关的问题,帮助学生形成解决此类问题的能力:
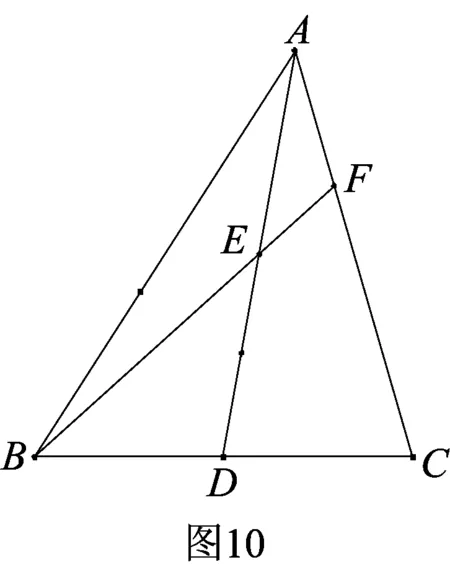
1.已知:如图10,△ABC中,D是边BC的中点,E是AD的中点,BE的延长线交AC于点F,求AF∶FC的值.
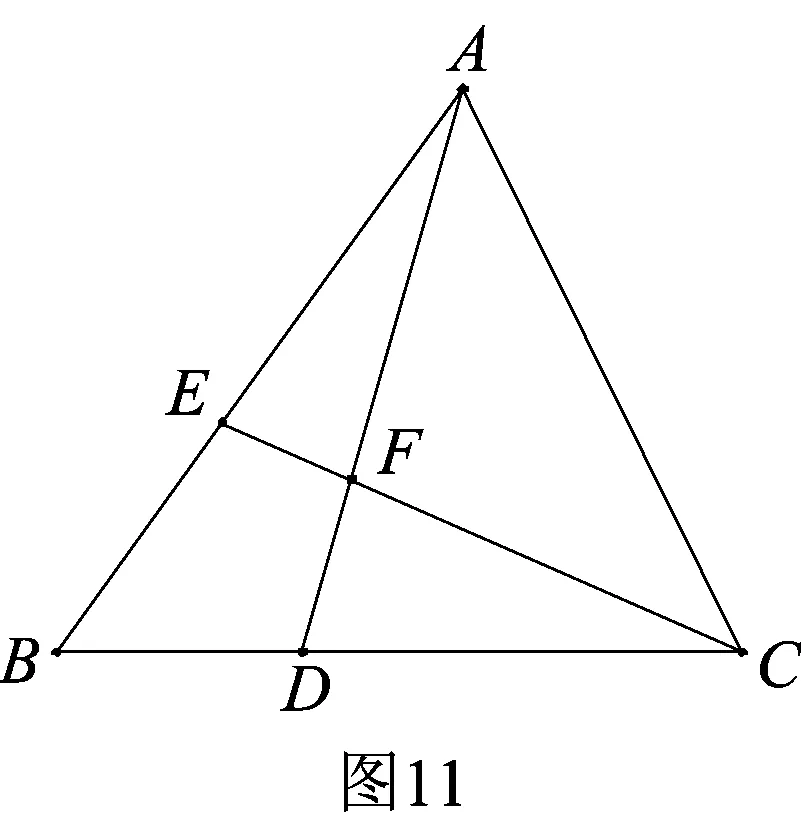
2.已知:如图11,△ABC中,D、E分别是边BC、AB上的两点,AD、CE交于点F,且BD∶DC=1∶2,BE∶AE=2∶3,求AF∶FD的值.
4“巧练”要着眼学生的发展,促进数学素养的提升.
数学教育不是“毕其功于一役”的教育,应该是“风物长宜放眼量”的教育,数学学习要着眼于学生的终身发展,要致力于学生数学素养的提升.要实现这一目标,就应该抓住核心概念组织教学,练习中就要围绕这些核心概念编制问题,将核心概念融入到学生对新知识的理解、运用之中.如在学习了《等腰三角形》一课后,老师安排了如下练习.
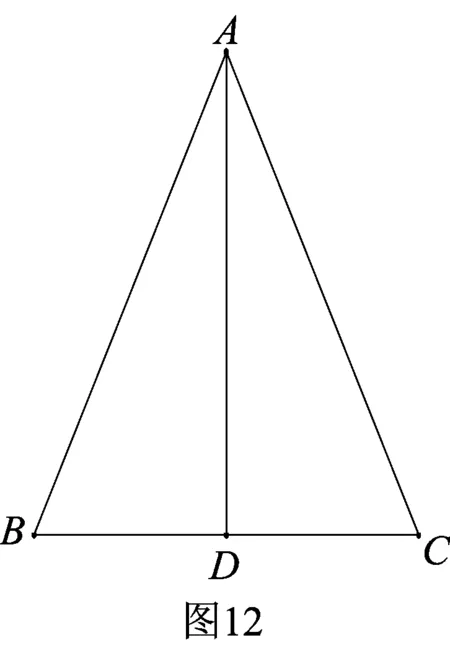
案例6如图12,在ABC中,AB=AC.
(1)∵AD⊥BD,∴∠____=∠____;____=____.
(等腰三角形底边上的高与____、____重合).
(2)∵AD是中线,∴____⊥____;∠____=∠____.
(等腰三角形底边上的中线与____、____重合).
(3)∵AD是角平分线,∴____⊥____;____=____.
(等腰三角形顶角的平分线与____、____重合).
这组题的目的是复习等腰三角形“三线合一”的性质,同时对数学中的“文字语言”、“图形语言”和“符号语言”的相互转化进行训练,通过填空,有效的训练学生用“数学符号”来表示数学的逻辑推理能力,可谓“举重若轻”.又如学习《用字母表示数》之后,布置如下问题:
案例7 (1)用计算器计算12×18,25×25,37×33,41×49,56×54,63×67,…,并探索规律,尝试再写出两个式子.
(2)用含字母的代数式表示运算规律,并说明规律的正确性.
问题(1)的目的是引导学生学会观察,学会思考,逐步培养发现问题的能力.通过观察、计算可以发现,这几个两位数乘两位数的算式中,十位数字相等,个位数字之和为10,积是三位或四位数,积的后两位恰好是因数个
位数字之积,前面一位或两位等于因数十位数字乘以比它大1的数的积.问题(2)是用数学符号语言表述发现的规律,其目的是培养学生提出问的能力.设一个因数的十位数字是a,个位数字是b,则以上规律可表示为:
(10a+b)[10a+(10-b)]=100a(a+1)+ab.
如果发现规律,并提出了问题,那么分析和解决它就比较容易了.这种发现问题、提出问题、分析问题和解决问题的能力是我们要致力培养的“四种能力”,它们是学生终身发展所需要的重要素养.我们只有在日常的教学活动中精心准备,巧妙设计,有效点拨,才有可能使学生在潜移默化的学习活动中发展和提升自身的数学素养.
“巧练”离不开“深备”,也离不开“先学”和“精导”,要达到“增效减负”的目的,教师必须充分把握教学内容的内涵,对准教学重难点,深刻理解教学内容所蕴含的思想方法,巧妙设置具有典型性、代表性的问题,让学生通过有效训练,达到“解一题,通一类,会一片”的效果.
参考文献
1史宁中.基本概念与运算法则——小学数学教学中的核心问题.北京:高等教育出版社,2013
2中华人民共和国教育部制定.义务教育数学课程标准(2011年版).北京:北京师范大学出版社,2012
基金项目:安徽省教育规划课题一本真性数学课堂教学模式的实践研究(课题编号:JG13236).
(收稿日期:2016-02-24)
参考
