三角形分割成两个等腰三角形的条件探究

安徽省合肥市第四十八中学　　陶兴高　　何军成　　(邮编：230061)



三角形分割成两个等腰三角形的条件探究

安徽省合肥市第四十八中学陶兴高何军成(邮编：230061)

“综合与实践”课是以具体问题为载体，学生经历设计解决问题方案，并加以实施的过程，体验建立模型、解决问题的过程，且在过程中不断总结反思，尝试发现和提出问题，是帮助学生获得数学活动经验的重要途径．在“综合与实践”课上学生通过对有关问题的探讨，结合已有的知识和生活经验，通过独立思考或与他人合作，感悟数学各部分之间的联系、数学与生活之间的联系，从而激发数学学习的兴趣，加深对所学数学内容的了解，发展应用意识和能力．

下面笔者以一节“综合与实践”课，即“三角形分割成两个等腰三角形的条件探究”为例，谈谈对“综合与实践”课的一些设想和思考．

1“三角形分割成两个等腰三角形的条件探究”的教学主要过程

1.1情境创设

教师：同学们，我们学习三角形时，有时会遇到一些三角形，它们可以分割成两个等腰三角形，有的却不可以，一个三角形能否分割成两个等腰三角形显然与该三角形满足的条件有关，本节课我们将通过动手画图、认真思考，并利用我们已有的知识来共同探究三角形能分割成两个等腰三角形的条件．

1.2共同探究

环节1复习相关知识，初步体验“分割”

教师：顶角为36°或108°的等腰三角形也叫做“黄金三角形”，你能求出黄金三角形的底角吗？你是怎样求的？

学生1：当顶角为36°时，这个“黄金三角形”的底角为72°，当顶角为108°时，这个“黄金三角形”的底角为36°．当已知顶角，可以根据利用三角形内角和定理求出两个底角的和，又因为“等腰三角形的两个底角相等”，可求出底角的度数．

教师：很好，显然在等腰三角形中，已知顶角的度数可以求出底角的度数，另外也可以已知底角的度数求出顶角的度数．

教师：如图1所示，△ABC为黄金三角形，其中∠A=108°，∠B=∠C=36°，作底角∠ABC的角平分线BD，可将△ABC分割成两三角形△ABD和△DBC，说一说这两个三角形各角的度数？△ABD和△DBC是等腰三角形吗？

学生3：△ABD中，∠A=∠ABD=36°，∠ADB=108°；△DBC中，∠C=∠BDC=72°，∠DBC=36°.根据“等角对等边”，它们都是等腰三角形.

教师：显然图1所示的“黄金三角形”是可以分割成两个等腰三角形的，分割线就是底角平分线.

(说明：过三角形一个顶点作一直线，将该三角形分割成两个三角形，顶点和对边交点之间的线段，本文中称之为“分割线”)

活动意图本环节是通过介绍“黄金三角形”(也是等腰三角形)，巩固等腰三角形的相关知识，即三角形的内角和定理、“等边对等角”和“等角对等边”等．它们是本节数学活动课的知识基础；通过了解顶角为36°的“黄金三角形”的分割，让学生初步了解三角形分割成两个等腰三角形的情形，感知如何“分割”，为接下来的尝试“分割”作铺垫．

环节2先尝试“分割”，到会“分割”

教师：我们要探究出三角形分割成两个等腰三角形的条件，先要会“分割”，下面来看如图2所示，△ABC为“黄金三角形”，其中∠A=108°，∠B=∠C=36°，试将其分割成两个等腰三角形？

(教师巡视课堂，观察学生尝试“分割”的过程，适时启发、引导，鼓励同学之间相互交流)

教师：为实现上述活动的目标，实际上是找出什么？

学生4：找出分割线，且这条分割线将原三角形分割成两个分别有两个角相等的三角形．

教师：非常好，有同学找出分割线了吗？

学生5：我的分割线是AD，(给出图3)，其中△ABD中，∠B=∠BAD=36°，∠ADB=108°；在△ADC中，∠C=36°，∠CAD=∠ADC=72°．

学生6：我的分割线AD位置不同，(给出图4)其中△ABD中，∠B=36°，∠BAD=∠ADB=72°；△ADC中，∠C=∠CAD=36°，∠ADC=108°．

教师：两位同学的结果都是对的，根据等腰三角形的轴对称性可知，它们可看作为同一种情形．哪位同学能说一说你是怎样找的？

学生7：我是分情况讨论，首先过顶点A作分割线AD，使得AB=AD或AB=BD或AD=BD，即△ABD为等腰三角形，再通过计算角的度数来判断△ADC是否为等腰三角形，如果是，则可以确定这个三角形能被分割成两个等腰三角形；再分别过B、C作分割线，用同样的方法进行尝试．

教师：好，你很细心、认真，利用分情况讨论来进行尝试分割，看来我们对于一个三角形要讨论几次？

学生8：9次，但是有些情况不存在，可以不需要讨论下去，例如过顶点A的分割线AD，如果AD=AB，则C与D重合；过顶点B的分割线BE，如果AB=AM，则M与C重合；如果BA=BM，则∠BMA=∠BAC=108°，则△ABM的内角和大于180°；如果AM=BM，则∠ABM=∠BAC=108°，则△ABM的内角和大于180°；过顶点C作分割线，根据轴对称性，情形与过顶点B作分割线一样．

教师：看来同学们在尝试分割的过程中探讨和交流得很深入、很全面，大家基本上掌握了分割的方法．例如尝试分割△ABC，先过顶点A作分割线，具体操作过程如下图所示，再分别过B、C作分割线，以相同方法分析．

教师：刚才的探究让我们知道了怎样找出分割线，将三角形分割成两个等腰三角形．下面我们来试着将如图5所示的△DEF(∠D=60°，∠E=40°，∠F=80°)分割成两个等腰三角形？

……

(具体操作探究过程与上例大致相同，此处不再赘述)

活动意图本环节是对两个具体三角形进行分割，第一个是顶角为108°“黄金三角形”，因为该三角形是特殊的等腰三角形，对其进行尝试分割，过程较为简单，学生容易取得成功，从而能激发学生进一步探究的欲望，同时也获取了将三角形分割两个等腰三角形的一般程序和方法，积累操作经验．第二个三角形为不等边三角形，对它的分割则是巩固刚刚获得的方法，并进一步增强分割三角形的操作体验．

环节3猜想能“分割”的条件，并证明

教师：下图是刚才出现的能分割成两个等腰三角形的三个三角形，仔细观察，你能猜想出三角形分割成两个等腰三角形的条件吗？

学生9：我的猜想是“当三角形中有一个角是另一个角的2倍时，这个三角形能够分割成两个等腰三角形，此时的分割线过第三个顶点”．

教师：很好，你会证明吗？

学生10：会，(结合所画图)设∠B为α，∠C为2α，AD为分割线，且令AD=BD(△ABD为等腰三角形)，则有∠BAD=∠B=α，所以∠ADC=∠BAD+∠B=2α，所以∠BDC=∠C=2α，所以△BDC也是等腰三角形．

教师：太好了，有猜想，有证明．你在什么时候就有这样的猜想了？

学生11：在画图尝试分割时，就有这样的猜想．

教师：看来同学们在尝试分割时不仅认真操作，而且还认真思考．是不是“只要三角形中有一个角是另一个角的2倍时，这个三角形就一定能够分割成两个等腰三角形”呢？

学生12：还要加一个条件，2倍角必须是锐角，因为如果2倍角是直角或钝角时，不可能作为等腰三角形的底角．

教师：分析的很有道理，这样我们就得到结论1“当三角形中有一个角是另一个角的2倍，且2倍角为锐角时，这个三角形能够分割成两个等腰三角形，此时的分割线过三个顶点”．还有其他的猜想吗？并能证明吗？

学生13：我的猜想是“当三角形中有一个角是另一个角的3倍时，这个三角形能够分割成两个等腰三角形，此时分割线过3倍角的顶点”．

教师：好，没有其他条件的补充，那么怎样证明？

学生14：(结合所画图)设∠B为α，∠ACB为3α，CD为分割线，且令CD=BD(△BDC为等腰三角形)，则有∠DCB=∠B=α，所以∠ADC=∠DCB+∠B=2α，∠ACD=∠ACB-∠DCB=2α，所以∠ADC=∠ACD=2α，所以△ADC也是等腰三角形．

教师：这样我们得到结论2“当三角形中有一个角是另一个角的3倍时，这个三角形能够分割成两个等腰三角形，此时分割线过3倍角的顶点”．同学们还有其他的猜想或发现吗？

……(学生吃惊、疑惑)

教师：图6、图7和图8中的三个三角形，它们的分割线在两个等腰三角形中，分别作为什么身份出现？

学生15：分割线有时在两个等腰三角形中均为腰，有时为其中一个的底，为另一个的腰．(此时出示图6、图7和图8中各分割线的身份说明)

教师：那么有可能存在一个三角形，能分割成两个等腰三角形，且分割线均为两个等腰三角形的底吗？

学生16：不存在，(结合所画图)假设△ABD和△ADC为等腰三角形，分割线AD均为二者的底，则∠BDA=∠BAD，∠CDA=∠CAD，又因为∠BDA+∠CDA=180°，所以∠BAD+∠CAD=180°，则三角形内角和大于180°，这显然不可能．

教师：很好，利用反证法来证明．还有其他情形吗？

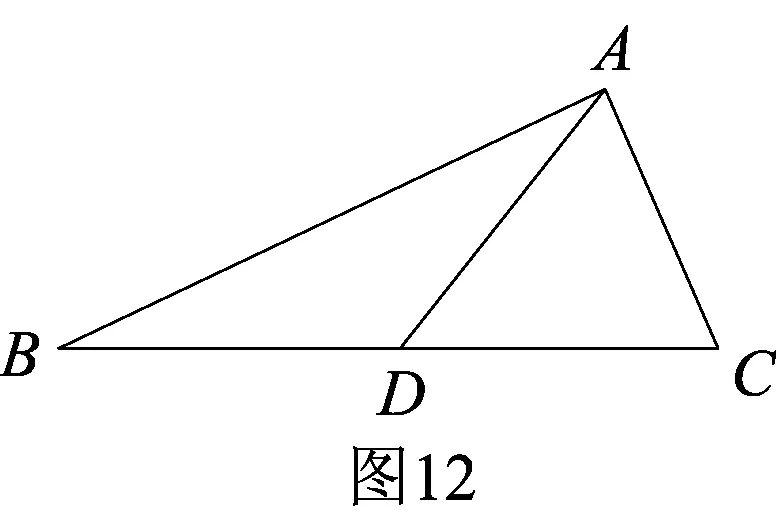
学生17：我发现还有一种情况，分割线同时为两个等腰三角形的腰，但是它们的顶角顶点是同一点，这与已经分析过的分割线同时是两个等腰三角形的腰，但是它们的顶角顶点不是同一点这情形不一样，(结合所画图)△ABD和△ADC均为等腰三角形，其中DA=DB，CA=CD(点D同为两个等腰三角形的顶角顶点)，设∠B为α，∠C为β，则∠B=∠BAD=α，∠C=∠CAD=β，又因为∠B+∠C+∠CAB=180°，所以∠B+∠BAD+∠C+∠CAD=2α+2β=180°，即α+β=90°，所以我发现所有直角三角形都能分割成两个等腰三角形，此时分割线过直角顶点(结论3)．

(教室响起了热烈的掌声)

教师：老师也由衷为你喝彩，欣赏你会观察，会发现，并会分析问题和解决问题．下面我们来总结一下我们的探究结果：

根据“分割线的出现时身份”可知，它只有四种可能：分割线均作为腰，它的两个端点分别为顶角顶点；分割线均作为腰，它的某一端点同时作为顶角顶点；既作为腰，又作为底；同时作为底．四种情形我们都已探究过，所以我们今天这节课“三角形分割成两个等腰三角形的条件”的探究已经结束……

图形能分割的条件其中一个角是另一个角的2倍,其中2倍是锐角其中一个角是另一个角的3倍直角三角形分割线的位置过第三个角的顶点过3倍角的顶点过直角顶点分割线出现时的身份均作为腰,分割线的两个端点分别为顶角顶点既作为腰,又作为底均作为腰,分割线的某一端点同时作为顶角顶点

活动意图通过展示上一环节出现的能分割成两个等腰三角形的三个三角形，引导学生仔细观察，回忆“分割”操作的过程，利用操作过程中的经验和感悟，提出“猜想”，并证明、归纳得到结论1和结论2；通过提问“能分割成两个等腰三角形的三个三角形，它们的分割线在两个等腰三角形中，分别作为什么身份出现？”引导学生观察、对比和思考，发现还有另外两种情况(情况一：分割线是两个等腰三角形的底；情况二：分割线同时作为两个等腰三角形的腰，分割线的某一端点同时作为两个等腰三角形顶角顶点)，并进行分析、证明，获得结论3．从通过“尝试分割”收获操作感悟来探究条件，到“假设能分割，分割线可能具有的身份”来探究条件，方式发生了改变，难度增加，但却让学生清楚，我们已经探究出全部情形.另外这样设计有助于培养学生的发现问题、提出问题和解决问题的能力，有助于培养学生逻辑思维的严密性和完善性．

2点评

《数学课程标准(2011年版)》指出：数学活动经验的积累是提高学生数学素养的主要标志.帮助学生积累数学活动经验是数学教学的重要目标，是学生不断经历、体验各种数学活动过程的结果.“综合与实践”是积累数学活动经验的重要载体.本节课的教学围绕“三角形能分割成两个等腰三角形的条件探究”这一问题核心，开展了一系列数学活动.在整个探究过程中，真正体现出实践活动为手段，具体问题为载体，积累数学活动经验为目的的教学特点与形式．在学生积累数学活动经验方面，这节课具体体现了以下几点：

2.1在“操作”与“思考 ”中，积累活动操作的经验

经验离不开活动，数学活动是经验产生的源泉，因此离开了数学活动，就根本不会形成有意义的数学活动经验，只有亲身经历体验了才能形成经验．本节课，学生首先通过观察顶角为36°的“黄金三角形”的分割情形，初步体会分割，接着让学生从简单而易操作的顶角为108°的“黄金三角形”进行实践(动手画)、观察分析(动眼看)、计算(动笔算)、思考(动脑想)，得到将三角形分割成两个等腰三角形的一般程序和方法，再尝试分割第二个三角形(三个内角分别为40°、60°和80°)，进一步巩固和加深前面的操作经验和体验．这一系列具体操作和思考活动，让学生会借助数据进行数学思考，积累了根据特例概括一般规律的经验，进一步提升了抽象、概括、判断等思维能力．

2.2在“反思”中，积累解决问题的经验

我国著名数学教育家曹才翰先生曾经提过“培养学生对学习过程进行反思的习惯，提高学生的思维自我评价水平，这是提高学习效率，培养数学学习能力的行之有效的方法”.本节课要解决的问题是探究三角形分割成两个等腰三角形的条件，问题的解决是基于学生有两点生成：第一，会利用上一环节尝试“分割”的操作过程中所积累的经验和感悟，进行归纳反思，猜想出三角形能分割成两个等腰三角形的可能具有的条件(结论1，结论2)；第二，对于“直角三角形能分割成两个等腰三角形”(结论3)的探究，在没有具体实例尝试“分割”的经历的情况下，通过对比分割线出现时的身份不同，反思发现还可能有的情形，即“分割线均作为腰，它的其中一端点同时作为两个等腰三角形顶角顶点”．在上述问题解决的过程中，学生不断地进行归纳、对比、概括等活动，并据此提出猜想，证明猜想，并对猜想作必要的修改完善.这种对刚刚经历的活动过程(条件、步骤、方法等)的反思，有助于让学生积累解决问题的经验.

2.3在“做数学”中，积累问题探究的经验

建构主义指出：数学学习并非是一个被动的接受过程，而是一个主动的建构过程.也就是说数学知识必须基于个人对经验的操作、交流，通过反思来主动建构.教师应努力给学生搭建“自主学习”的平台，从而有效地让学生领悟数学思想和数学方法，启发学生积极思维，引导学生自己探索、发现新知识，积累数学活动经验.根据本节课所探究的问题的特点，教师合理设计数学活动环节，让学生经历了“做数学”式的探究数学问题的过程：提出问题(探究三角形分割成两个等腰三角形的条件)→分析问题(感受“分割”，尝试“分割”)→解决问题(提出猜想，并予以证明，归纳结论).在探究过程中，学生可以体会：问题解决与什么元素有直接关联，问题解决的关键是什么，问题解决的方法有哪些等等.显然学生在以“做数学”的形式进行数学探究，不仅高效地解决了问题，同时还积累问题探究的经验.

(收稿日期：2016-03-15)