高二数学测试

高二数学测试

一、填空题(本大题共14小题,每小题5分,共70分)

2.有不同颜色的上衣5件,裤子3条,从中选一件送给某人,共有______种不同的选法；从中选出一套送给某人,共有______种不同的选法.

3.“∵四边形ABCD是矩形,∴四边形ABCD的对角线相等”,以上推理的大前提是______.

4.用反证法证明“方程F(x)=0至少有两个实根”,其反证假设是______.

6.把体育组9个相同的足球放入编号为1、2、3的三个箱子里,要求每个箱子放球的个数不少于其编号数,则不同的放法共有______种.

8.若把单词“error”中字母的拼写顺序写错了,则可能出现的错误的种数是______.

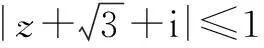
10.从4名男生和2名女生中任选3人参加演讲比赛,所选3人中至少有1名女生的方案总数是______.

11.若 5名同学安排在星期一至星期五值日,每人一天,若甲同学不能排在星期一,乙同学不能排在星期五,则共有______种不同的值日方法.

12.在平面几何中,有射影定理:“在∆ABC中,AB⊥AC, 点A在BC边上的射影为D,有AB2=BD·BC.”类比平面几何定理,研究三棱锥的侧面面积与射影面积、底面面积的关系,可以得出的正确结论是:“在三棱锥A-BCD中,AD⊥平面ABC,点A在底面BCD上的射影为O,则有______.

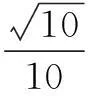
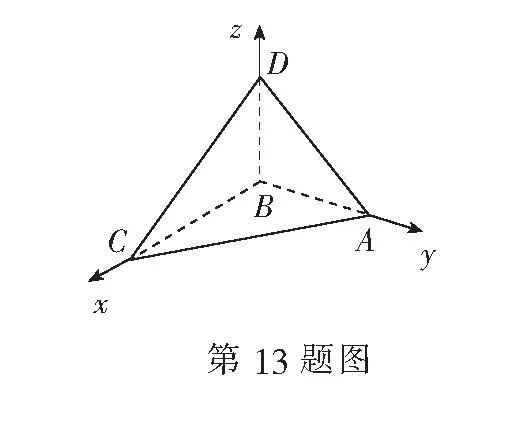
14.足球比赛的计分规则是:胜一场得3分,平一场得1分,负一场得0分,那么一个队打14场共得19分的情况共有______种.

二、解答题(本大题共6小题，共90分.解答应写出文字说明、证明过程或演算步骤)

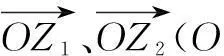
16.(本小题满分14分)A,B,C,D,E五人站成一排.

(1)A,B两人相邻的不同排法有多少种?

(2)A,B,C两两不相邻的排法有多少种?

(3)A,B都与C相邻的不同排法有多少种?

(4)A,B,C顺序一定的排法有多少种?

18.(本小题满分15分)观察下列三角形数表

1 …………第1行

2 2 ……… 第2行

3 4 3 …… 第3行

4 7 7 4 ……第4行

5 11 14 11 5…第5行

… … … …

假设第n行的第二个数为an(n≥2,n∈N*),

(1)依次写出第六行的所有6个数字;

(2)归纳出an+1与an的关系式，并求出an的通项公式;

(3)设anbn=1,求证:b2+b3+…+bn<2.

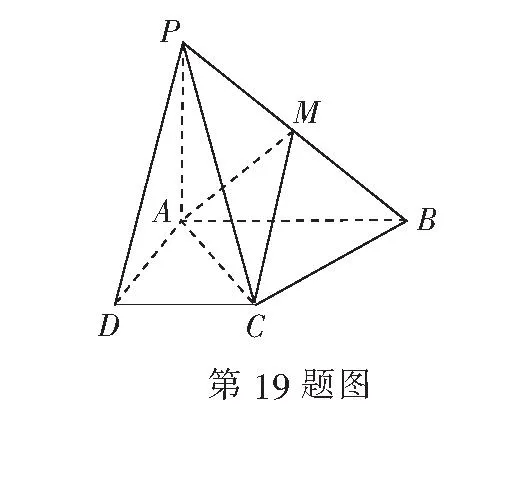
19.(本小题满分16分)已知四棱锥P-ABCD的底面为直角梯形,AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=1，AB=2，M是PB的中点.

(1)求AC与PB所成角的余弦值；

(2)求面AMC与面BMC所成二面角的余弦值的大小.

20.(本小题满分16分)在1与2之间插入n个正数a1,a2,…,an,使这n+2个数成等比;又在1与2之间插入n个正数b1,b2,…,bn,使这n+2个数成等差.记An=a1a2…an,Bn=b1+b2+…+bn.

(1)求数列{An}和{Bn}的通项;

(2)当n≥7时,比较An与Bn的大小,并证明你的结论.