柯西不等式在高中数学解题中的应用

王含阳　徐璐路　俞晓英

(江苏省扬州大学数学科学学院数学与应用数学13级2班,225002)

柯西不等式在高中数学解题中的应用

王含阳徐璐路俞晓英

(江苏省扬州大学数学科学学院数学与应用数学13级2班,225002)

众所周知,不等式是中学数学的基础知识,也是高中数学课程中的重点和难点,它不仅渗透到了中学数学课本的各个章节,而且在实际问题中被广泛应用．其中,柯西不等式作为重要的不等式之一,其形式丰富多样,应用灵活广泛．

柯西不等式的一般形式为

柯西不等式在证明不等式、解三角形、求函数最值、解方程等方面得到应用．若能巧妙应用柯西不等式,掌握其思想方法,则许多复杂问题会简单化,同时又能拓宽解题思路,提高学习效率．分类举例说明如下:

一、柯西不等式在代数中的应用

1. 求最值

例1已知a+b+c+d+e=8,a2+b2+c2+d2+e2=16，求e的最大值与最小值．

2. 证明不等式

例2设a，b，c，d是正数,a+b+c+d=1,求证:

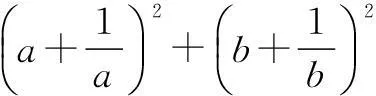
3. 解方程(方程组)

例3解方程：

解首先要使式子有意义,则

其次由柯西不等式,得

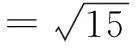
二、柯西不等式在几何中的应用

1. 推导点到直线的距离公式

证明设P1(x1,y1)是直线l上的任意一点,P(x0,y0)是坐标平面上的任意一点,那么

l:Ax1+By1+C=0,

①

②

|PP1|的最小值就是点P到直线l的距离.由柯西不等式，有

≥|A(x0-x1)+B(y0-y1)|

=|Ax0+By0+C-(Ax1+By1+C)|.

由①、②两式，得

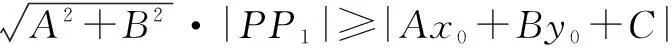
③

2. 推导点到面的距离公式

证明设Q(x,y,z)是平面π上的任意点,则Ax+By+Cz=-D且A2+B2+C2>0，

由柯西不等式，得

(A2+B2+C2)[(x-x0)2+(y-y0)2

+(z-z0)2]

≥[A(x-x0)+B(y-y0)+C(z-z0)]2

=[(Ax+By+Cz)

-(Ax0+By0+Cz0)]2

=[-D-(Ax0+By0+Cz0)]2

=(Ax0+By0+Cz0+D)2.

于是有

由垂线段最短，得

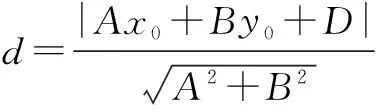
(本文系2015年扬州大学大学生科创项目研究成果之一，指导老师朱家生)