高三数学综合测试

高三数学综合测试

一、填空题(本大题共14小题,每小题5分,共70分)

3.已知l1:x+ay+6=0和l2:(a-2)x+3y+2a=0，则直线l1∥l2的充要条件是a=______.

4.设x∈{-1,1},y∈{-2,0,2}，则以(x,y)为坐标的点落在不等式x+2y≥1所表示的平面区域内的概率为______.

5.根据如图所示的伪代码,可知输出的结果S为______.

第5题图

6. 一个样本a,3,4,5,6的解的平均数是b,且不等式x2-6x+c<0的解集是(a,b)，则这个样本的标准差是______.

8.已知P是直线l:kx+y+4=0(k>0)上一动点,PA,PB是圆C:x2+y2-2y=0的两条切线,切点分别为A,B.若四边形PACB的最小面积为2,则k=______.

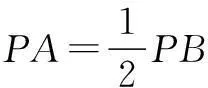
13.设定义在R上的函数f(x)满足f(0)=1,若对任意的x∈R,都有f(x+2)-f(x)≤5·3x,f(x+4)-f(x)≥50·3x,则f(8)=______.

14.已知函数

若函数y=f(f(x)-a)有四个零点，则实数a的所有可能取值构成的集合是______.

二、解答题(本大题共6小题，共90分.解答应写出文字说明、证明过程或演算步骤)

(1)求ω的值，并求函数f(x)在区间[0,π]上的单调增区间；

16.(本小题满分14分)如图,在四棱锥P-ABCD中,O为AC与BD的交点,AB⊥平面PAD,∆PAD是正三角形,DC∥AB,DA=DC=2AB.

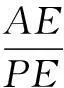
(2)求证:平面PBC⊥平面PDC.

17.(本小题满分15分)某中学校园内原有一块四分之一圆面形状的草坪AMN，如图(1),其中AM=AN=8 m,∠MAN=90°.今年暑假整治校园环境时,为美观起见,学校设计将原有草坪扩大,具体实施方案是:从圆弧上一点P作圆弧的切线BD,分别与AM,AN的延长线交于点B，D,并以AB,AD为邻边构造矩形ABCD,再以C为圆心制作一块与AMN形状相同的草坪,构成矩形绿地ABCD(如图(2)).

(1)求矩形绿地ABCD占地面积的最小值；

(2)若由于地形条件限制,使得矩形一边AB的长度不能超过10 m,求此时矩形绿地ABCD占地面积的最小值.

(1)求椭圆E的标准方程;

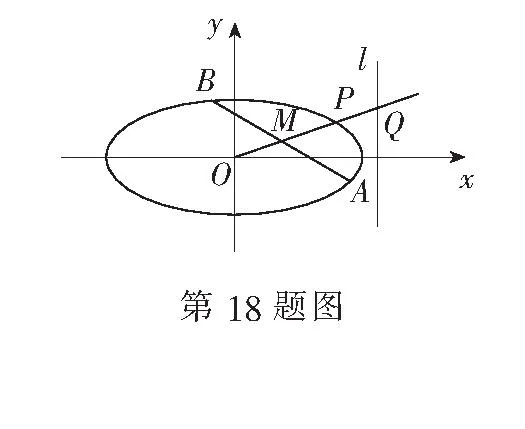
19.(本小题满分15分)已知数列{an}中，a1=3,a2=5,{an}前n项和Sn,满足Sn+Sn-2=2Sn-1+2n-1(n≥3).

(1)求数列{an}的通项公式;

20.(本小题满分16分)己知函数

(1)若f(1)=0,求函数f(x)的单调递减区间;

(2)若关于x的不等式f(x)≤ax-1恒成立,求整数a的最小值；

(3)若a=-2,正实数x1,x2满足f(x1)+f(x2)+x1x2=0,证明:

参考答案

一、填空题

二、解答题

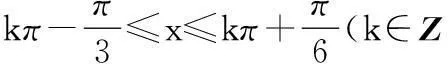
16.(1)因为OE∥平面PBC,OE⊂平面PAC,平面PAC∩平面PBC=PC,所以OE∥PC,

所以AO∶OC=AE∶EP.

在正三角形PAD中,M为PD中点,所以AM⊥PD.因为AB⊥平面PAD,所以AB⊥AM.

又因为DC∥AB,所以DC⊥AM.

因为BF∥AM,所以BF⊥PD,BF⊥CD.

又因为PD∩DC=D,PD、DC⊂平面PCD,所以BF⊥平面PCD.因为BF⊂平面PBC,所以平面PBC⊥平面PDC.

17.(1)设AB=a,AD=b,矩形绿地ABCD占地面积为S,则

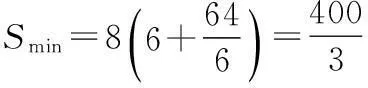
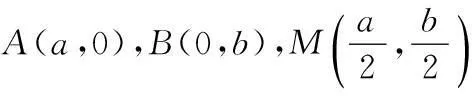
(5k2+1)x2+10mkx+5m2-50.

当Δ>0，5k2-m2+1>0时，

∵OP是OM，OQ的等比中项，

∴OP2=OM·OQ，

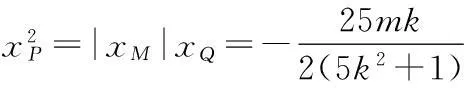
19.(1)由Sn+Sn-2=2Sn-1+2n-1(n≥3),得

Sn-Sn-1=Sn-1-Sn-2+2n-1(n≥3),

所以an=an-1+2n-1(n≥3),

累加得an=2n+1.

所以Tn=b1+b2+…bn

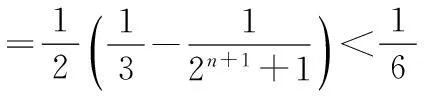
因为Tn+1-Tn>0,所以{Tn}递增.

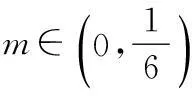
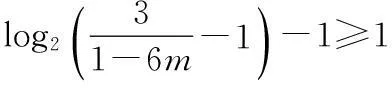
f(x)=lnx-x2+x,x>0,

由f′(x)<0,得2x2-x-1>0.

又x>0，所以x>1，

所以f(x)的单调减区间为(1，+∞).

(2)方法1：令g(x)=f(x)-(ax-1)

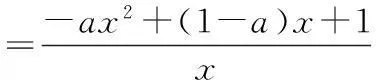
当a≤0时，因为x>0,所以g′(x)>0,所以g(x)在(0,+∞)上是增函数.

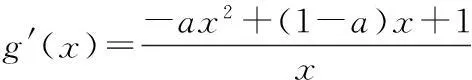
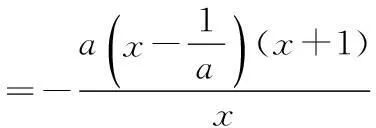
故函数g(x)的最大值为

所以当a≥2时，h(a)<0，

所以整数a的最小值为2.

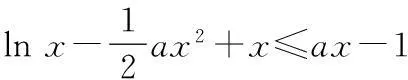
在(0，+∞)上恒成立.

当x∈(0,x0)时，g′(x)>0;

当x∈(x0,+∞)时，g′(x)<0,

所以g(x)在x∈(0,x0)上是增函数；在x∈(x0,+∞)上是减函数.

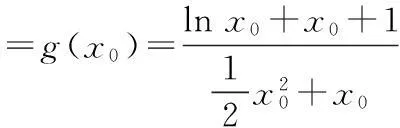
所以，a≥2，即整数a的最小值为2.

(3)当a=-2时，f(x)=lnx+x2+x,x>0.

由f(x1)+f(x2)+x1x2=0,即lnx1+x21+x1+lnx2+x22+x2+x1x2=0,从而

(x1+x2)2+(x1+x2)=x1·x2-ln(x1·x2).

令t=x1·x2,则由φ(t)=t-lnt，得

可知，φ(t)在区间(0，1)上单调递减，在区间(1，+∞)上单调递增，

所以φ(t)≥φ(1)=1,

所以(x1+x2)2+(x1+x2)≥1,