让探究性问题串引领数学概念的构建——函数概念的课堂教学设计

陈海波

(江苏省盱眙中学，211700)

○教学研究○

让探究性问题串引领数学概念的构建

——函数概念的课堂教学设计

陈海波

(江苏省盱眙中学，211700)

函数的概念是中学数学的基本概念.高中阶段不仅把函数看成变量之间的依赖关系,同时还用集合与对应的语言刻画函数.在本文中,笔者在高中函数概念教学设计中引入探究式教学模式,尝试用探究性问题串引领数学概念的构建.

一、问题的提出

新课程标准强调探究性教学要让学生像科学家从事科学研究那样来学习科学,领悟科学研究的真谛.但是在我们目前的中小学教学中,现状往往是另外一种景象,照本宣科压抑了学生的数学学习兴趣;缺乏问题意识不利于创新精神和实践能力的培养;不重视基本概念、核心数学思想的教学不利于学生数学素养的提高.因此在我们的教学中应不断改进教学方式，培养学生的创新能力，提高学生数学素养.实践证明探究和问题串教学是一种行之有效的教学方式.

1. 探究性教学

数学教育对培养学生的创造能力肩负着特殊的责任. 近年来，人们越来越关注探究性教学，认为离开探究性教学就没有思维的广阔空间，就没有鲜活的思维火花，就不可能有创造能力的培养和提升.在概念的教学中，如何产生概念的过程就是一种探究过程.这样的探究过程不仅能促进学生对数学概念的理解，而且能很好地培养学生的学习兴趣，对学生发现能力和创造能力培养是十分有益的.

2. 问题串教学

问题是数学思维活动的载体，而课堂的重要构成因素就是问题.孤立的问题对思维发展几乎没有什么作用，只有让问题以问题串的形式出现，在问题串的引领下，让学生进行系统的连续的思维活动，学生的思维才能不断攀升到新的高度.所以问题串不是几个问题的简单组合，而是指在一定的学习范围和主题之内， 按学情、教学目标、对一节课的教学内容或主题，设计一组具有较强逻辑关联的问题，问题串的教学是一种符合当前新课程改革要求的教学模式.

二、教学设计

1. 教材分析

本节课是苏教版必修1第二章第一节内容.数学课程标准对函数概念教学的要求是:通过丰富的实例,进一步体会函数是描述变量之间依赖关系的重要模型,在此基础上学习用集合和对应的语言来刻画函数.其核心内涵为非空数集到非空数集的一个单值对应,它不仅对前面学习的集合作了巩固和发展，而且它是学好后继知识的基础和工具.

2. 学情分析

学生在初中初步探讨了函数的相关知识的基础上,通过必修1第一章“集合”的学习,对集合思想的认识也日渐提高,为重新定义函数,从根本上揭示函数的本质提供了知识保证.通过以前的学习,学生已有一定的分析、推理和概括能力,初步具备了学习函数概念的基本能力.

3. 目标分析

(1)知识与技能:体会函数是描述变量之间的依赖关系的重要数学模型,理解函数的概念.

(2)过程与方法:让学生经历函数概念的形成过程,函数的辨析过程,函数定义域的求解过程以及求函数值的过程，渗透归纳推理、发展学生的抽象思维能力.

(3)情感态度价值观:通过经历以上过程,让学生体会函数是描述变量之间的依赖关系的重要数学模型.在此基础上学会用集合与对应的语言来刻画函数,体会对应关系在刻画函数概念中的作用;体验函数思想;通过师生互动、生生互动，让学生在民主、和谐的课堂氛围中感受数学的抽象性和简洁美.

4.教学过程设计

(1) 问题情境

事物都是运动变化着的，我们可以感受到它们的变化.

早晨太阳从东方冉冉升起;

气温随着时间在悄悄地改变;

随着二氧化碳的大量排放地球正在逐渐变暖;

中国的国内生产总值在逐年增长;

……

问题1你能仿照上面的句子仿写几句话吗?

设计意图让学生举例使其感受到现实生活中存在大量的变化关系从而为研究这类问题的重要性和必要性提供铺垫，这符合学生的认识规律.

在这些变化着的现象中，都存在两个变量.当一个变量变化时，另一个变量随之发生变化.

●怎样用数学模型刻画两个变量之间的关系?

●这样的数学模型具有怎样的特征?

●如何借助这样的模型来进一步描述和解释我们周围的世界呢?

追问请举出初中学过的一些函数.

初中函数的定义是什么?

y=0(x∈R)是函数吗?

设计意图通过回忆初中的函数及函数的定义,为三个实例的出现作好铺垫.由于受认知能力的影响,利用初中所学函数知识很难回答这些问题,形成认知冲突,让学生带着悬念、带着认知冲突学习后面的知识,这样有利于激发学生的学习欲望.

(2) 实例分析

现实生活中我们可能会遇到下列问题：

估计人口数量变化趋势是我们制定一系列相关政策的依据.从人口统计年鉴中，查得我国从1949年至1999年的数据资料如下表所示，你能根据这个表说出我国人口变化情况吗?

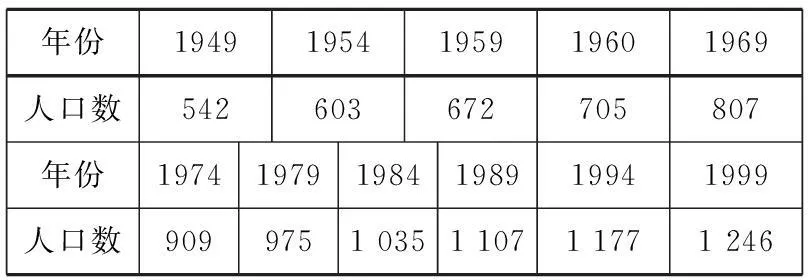
年份19491954195919601969人口数542603672705807年份197419791984198919941999人口数9099751035110711771246

问题2如果用x表示年份，y表示人口数，两个量x,y能构成函数吗?x和y的变化范围分别是什么?

追问如图1，如果把x的取值范围看成集合A，y的取值范围看成集合B，集合A中元素x与集合B中的元素有什么关系?

设计意图引导学生用集合与对应的语言来刻画上述实例.通过语言之间的转换,换一种说法,引出对应这一说法,为用对应描述变量之间的依赖关系奠定基础,同时培养学生分析问题和提取信息的能力.

在物理中我们还会遇到下面的问题：

一物体从静止开始下落，下落的距离y(m)与下落的时间x(s)之间近似地满足关系y=4.9x2.若一物体下落2s，你能求出它下落的距离吗?

问题3这里的变量x,y之间是否是函数关系？它们各自的变化范围是什么?试用集A,B表示(图2).

追问集合A中元素x与集合B中的元素有什么关系?

图3为某市24小时内的气温变化图.

(i)上午6时的气温约是多少?

全天的最高最低气温分别是多少?

(ii)在什么时刻气温为0℃?

(iii)什么时段内，气温在0℃以上?

问题4如果用x表示时间，y表示温度，两个量x,y构成函数吗?x和y的变化范围用集合A,B分别是什么?(图4)

追问集合A中元素x与集合B中的元素有什么关系?

(3) 构建数学

问题5以上三个实例有什么共同特点?

设计意图由前面三个实例, 借助三个集合单值对应关系图,抽象出函数概念的本质,这样处理有利于形成知识的正迁移.通过学生的“观察→分析→比较→归纳→概括”培养学生抽象思维的能力,同时也培养了学生的创新意识.

追问1你能用集合的观点给函数重新下个定义吗?

函数的概念:设A,B是非空的数集，如果按照某种对应法则f，对于集合A中的每一个元素x，在集合B中都有唯一的元素y和它对应，那么这样的对应叫做从A到B的一个函数，通常记为y=f(x),x∈A.其中集合A叫做函y=f(x)的定义域.

追问2概念中哪些地方要加强理解，请简要说明?

设计意图教师给出了概念,并不等于学生认识了概念,需要从不同的侧面,不同的角度去挖掘它,深化对概念的理解.一般来说先有理解再有认识,理解是过程,认识是结果.概念的认识应该从重要词句上剖析,找出其内涵和外延.

问题6如何理解符号f(1),f(f(1)),f(x)的含义?

设计意图加强理解用来表示对应关系的数学符号,制造了强烈的认知冲突,提出高认知水平的问题,引发学生的思考,激发学习动机与探究欲望.

追问我们把全体y值组成的集合称为函数的值域.函数的定义域、对应法则、值域统称为函数的三要素. 函数的值域与定义中的集合B关系如何?

(4) 理论应用

例1已知函数

(i)求函数的定义域;

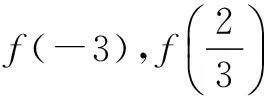
(iii)当a>0时,求f(a),f(a-1)的值.

(5)巩固练习

(ii)已知函数f(x)=3x3+2x,求f(2)+f(-a)的值.

设计意图在学习新知识的基础上,进行强化训练,使学生熟练掌握函数的概念,在强化的同时利用习题让学生很直观、形象地了解函数的三要素并理解函数的三要素.

(6) 小结及作业(略)

你还有哪些地方有疑问或不理解?你有哪些收获?

设计意图回顾在获得概念的艰苦曲折的历程中所用的认知思想,概括方法.体会数学总是从大量的具体实例出发,通过辨别,抽象,分化,提出假设,检验假设,再用符号语言规范化表达认知过程.

在数学课堂中,利用问题串进行探究减少了教师对知识的直接讲解,更多的是鼓励学生对问题进行深入思考;减少教师直接给出答案,更多的是引导学生发现、分析、解决问题.因此,这样的课堂中,学生的主体地位得以保证,大大激发了学生参与课堂的热情,学生得到了深刻的体验和感悟.最终,学生获得的不仅仅是数学知识,更不仅仅是会多做一些数学题目,更重要的是在这种过程中培养出来的数学兴趣和数学能力.