对一道高考题普适性特点的探究

黄高明

(福建省龙岩市新罗区教师进修学校，365400)

○高考之窗○

对一道高考题普适性特点的探究

黄高明

(福建省龙岩市新罗区教师进修学校，365400)

2015年全国高考课标Ⅰ卷理科数学第20题，是以抛物线为背景、以导数几何意义、直线与抛物线的位置关系为着力点命制的一道综合题．本题特点是题干清晰、设问精炼简洁,题目阅读量小,没有偏、烦、难、怪的味道,中规中矩,渗透了人文关怀的思想．此题重在考查学生的运算求解能力、推理论证能力、抽象概括能力；也考查了学生数形结合、函数与方程的、化归与转化等数学思想．此题第(2)小题虽然是考查直线和抛物线位置关系的一个结论,但笔者研究发现,直线在圆及其它圆锥曲线位置关系中也都具有这个普适性性质,让我们来慢慢揭开其中的奥秘吧．

一、原题回放及解答展示

(1)当k=0时,分别求C在点M和N处的切线方程;

(2)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由．

解题思路及解法分析第(1)题属容易题,根据导数几何意义即可获解．

第(2)题属稍难题,考查学生解决直线与圆锥曲线位置关系的常见方法,重在考查学生的探究能力；同时,也考查学生的运算求解能力、推理论证能力．本题渗透了数形结合、函数与方程、化归与转化等数学思想．常规思路是将∠OPM=∠OPN,转化为k1+k2=0,利用韦达定理可获解．

(2)存在符合题意的点,证明如下:

设P(0,b)为符合题意的点,M(x1,y1),N(x2,y2)，直线PM,PN的斜率分别为k1,k2.

将y=kx+a代入C的方程，得x2-4kx-4a=0，故x1+x2=4k,x1x2=-4a，

∴当b=-a时,有(k1+k2)=0,则直线PM的倾斜角和直线PN的倾斜角互补,

故∠OPM=OPN,所以存在P(0,-a)满足条件．

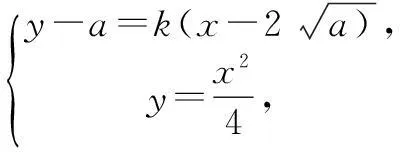
(2)存在符合题意的点,证明如下:

设P(0,n)为符合题意的点,M(x1,y1),N(x2,y2)，直线PM,PN的斜率分别为k1,k2,直线PM,PN的方程分别为y=k1x+n和y=k2x+n.

∵∠OPM=OPN，

∴原点到直线PM,PN的距离相等，

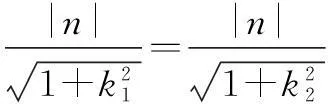
∴(k1-k2)(k1+k2)=0.

∵M,N是不同的两点,

∴k1≠k2，故有k1+k2=0.

以下同解法1．(略)．

二、题目变式推广

1.抛物线变式为具体椭圆

(2)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由．

(2)存在符合题意的点,证明如下:

(4+k2)x2+2kmx+m2-4=0.

由Δ=(2km)2-4(4+k2)(m2-4)

=16k2+64-16m2>0,

得m2<4+k2.

又∵k∈R,m>0，∴0

当m≥2时,不存在满足条件的点P．

注:以下所有变式及推广解答过程与此题基本相似,限于篇幅,均略去解答过程,只提供答案．

2.抛物线变为具体双曲线

(2)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由.

答案:(1)4. (2)当 0

本变式还可以变形为:

(2)试问y轴上是否存在点P,使得当k变动时,总存在以原点为圆心的圆与直线PN、PM都相切?

3.抛物线变为具体圆

变式4在直角坐标系xOy中,圆C:x2+y2=9与直线y=kx+m交于M,N两点.

(1)当m=6时,求直线和圆相切时的直线方程；

(2)试问y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由.

三、题目进一步纵深推广

(1)当直线经过F1时,求∆MNF2的周长；

(2)试问y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由．

解答过程略．

(1)当直线经过F1时,求F2M+F2N-MN的值；

(2)试问y轴上是否存在点P,使得当k变动时,总存在以原点为圆心的圆与直线PN、PM都相切?

解答过程略．

3.抛物线变为一般抛物线C:x2=2py(p>o)

变式7在直角坐标系xOy中,抛物线C:x2=2py(p>0)与直线y=kx+m(m>0)交于M,N两点.

(1)当k=0时,求曲线在M、N处的切线方程；

(2)试问y轴上是否存在点P,使得当k变动时,总存在以原点为圆心的圆与直线PN、PM都相切?

(2)存在点P(0,-m)满足条件．

4.抛物线变为一般圆C:x2+y2=R2

变式8在直角坐标系xOy中,圆C:x2+y2=R2与y=kx+m(m>0)交于M,N两点,

(1)当直线和圆相切时,试用R、k的代数式表示m；

(2)试问y轴上是否存在点P,使得当k变动时,总存在以原点为圆心的圆与直线PN、PM都相切?

由以上变式推广和纵深推广可知,本题所考察的性质不只抛物线有,对于一般的圆锥曲线都具有普适性．