关于数形结合的一点思考

夏炳文

(安徽省阜阳市第三中学，236000)

○短文集锦○

关于数形结合的一点思考

夏炳文

(安徽省阜阳市第三中学，236000)

著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休”,高度阐述了数和形在解决数学问题时的价值.最近在拜读了很多文章中关于对于“函数零点个数判别”或“图象交点个数判别”或“方程根的个数”这类问题的处理方法后,让笔者产生疑惑,仅仅通过函数图象加以处理,这样严谨吗?这是高考命题人的初衷吗?笔者通过如下一则案例,谈谈对这类问题的一点思考.

(1)求函数f(x)的解析式;

(2)判断函数f(x)在(0,π)内的零点个数,并加以证明．

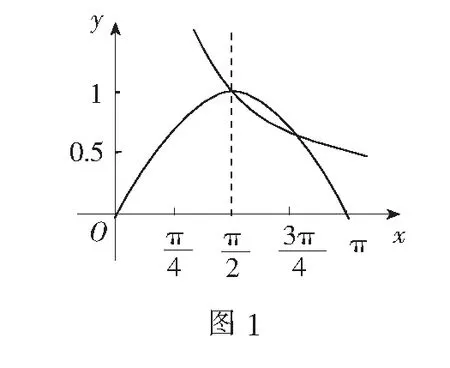
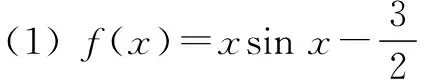
评注此解法通过将函数f(x)的零点个数转化为两个已知函数的交点个数,然后通过图象很容易得出有两个交点.但是作为一个压轴题,笔者认为这种解法并不是命题人命题时的初衷,何况命题人在第(2)问中特意加了一句:“并加以证明”.

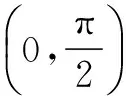
上述分析不仅严谨、自然,也符合学生的认知规律,正是基于形的直观性给解决问题明确了方向.由此发现,对于“函数零点个数判别”或“图象交点个数判别”或“方程根的个数”判别这类问题,我们可以先通过图象,直观感知结果,然后在图象的引导下利用单调性和零点的存在性定理加以处理.这样就可以培养学生从定形到定性再到定量研究数学问题的正确思维方式，完美地解决此类问题.