带限制条件的几类极值问题

张鲁西

(天津实验中学,300074)

带限制条件的几类极值问题

张鲁西

(天津实验中学,300074)

极值是中学数学中重要知识点之一,在实际生活中很多“最大”“最小”和“最优”问题都可以归结为极值问题.而这些问题的通常都是在某些特定环境和范围内产生的,这就自然出现了带限制条件的极值问题,即在条件B下,求对象A的最大或最小问题.此类问题广泛出现于各种奥数竞赛和高考命题,是中学数学学习的难点之一,解决这类问题的关键是如何合理地将将条件B应用于A的最大或最小问题的中．下面介绍几类带限制条件的极值问题的求法．

一、利用不等式求最值

运用不等式可以求极值问题,经常运用的不等式有:

(1)Cauchy-Schwartz不等式. 设a1,…,an,b1,…bn是实数,则

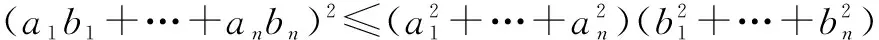
等式成立当且仅当存在实数k使得b1=ka1,…,bn=kan．

(2) 均值不等式. 设a1,…,an为非负实数,记

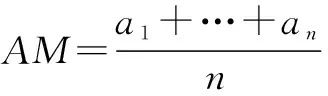
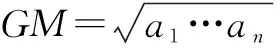
则有QM≥AM≥GM,且等式成立当且仅当a1=…=an．

例1设x,y,z是正数,且9x2+y2+16z2=1,求5x+2y+8z的最大值．

解利用Cauchy-Schwartz不等式及9x2+y2+16z2=1，得

(5x+2y+8z)2

≤((3x)2+y2

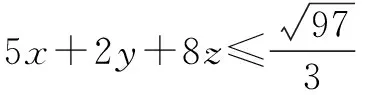
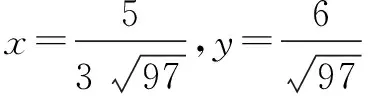
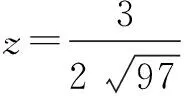
二、求三角函数最值

例2设α,β满足

求函数f(β)=2cos2β+cosβ的最大值．

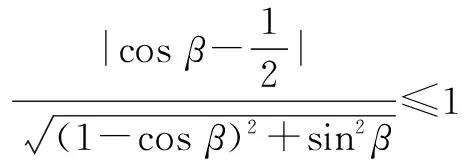
两边平方,整理得

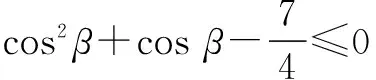
解不等式并注意|cosβ|≤1，得

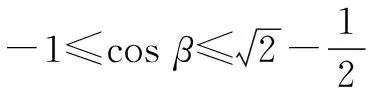
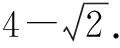
评注很多三角函数问题有几何背景,该题的已知条件在恰当变形后巧妙转化为解析几何问题,运用直线和曲线相交求出cosβ的取值范围,再利用二次函数的单调性得到最大值．

三、求与圆锥曲线相关的面积最值

在解析几何中也常见在限制条件下求二次曲线的最大面积问题．

例3求半径为R的半圆中与边界相切的椭圆的最大面积．

解在平面直角坐标系中,设半圆的方程为

椭圆方程为

则该椭圆与半圆在x轴上的边界相切,将半圆方程代入椭圆方程，得

(a2-b2)y2-2a2by+b2R2=0．

又半圆与椭圆相切,以上方程判别式为0,可得

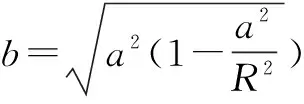
于是椭圆的面积

利用均值不等式，得

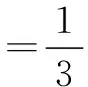
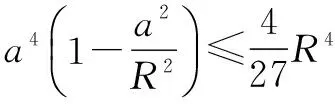
所以所求椭圆的最大面积为