高二数学测试

高二数学测试

一、填空题(本大题共14小题,每小题5分,共70分)

1.已知集合A={-1,0,2},B={2a},若B⊆A,则实数a的值为______.

3.函数y=3x-2的值域是______.

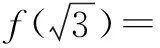
5.函数f(x)=x3+ax2+3x-9在x=3时取得极值,则a=______.

6.已知i为虚数单位,复数z满足(3+4i)z=25,则z的虚部为______.

8.若命题“∀x∈R,ax2-ax-2≤0”是真命题,则a的取值范围是______.

9.已知函数f(x)=ax3+x+1的图象在点(1,f(1))处的切线过点(2,7),则a=______.

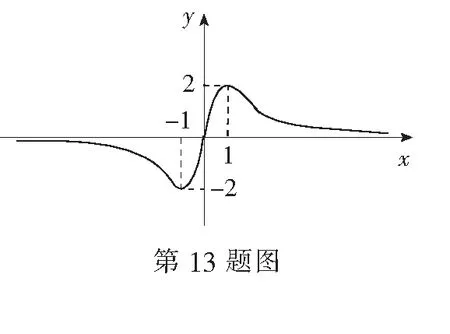
则不等式f(x)>-1的解集为______.

12.已知函数f(x)=x-1-(e-1)lnx,其中e为自然对数的底数,则满足f(ex)<0的x的取值范围是______.

二、解答题(本大题共6小题,共计90分,解答应写出必要的文字说明、证明过程或演算步骤)

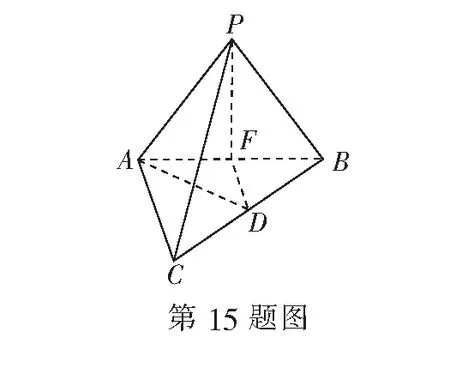
15.(本小题满分14分)如图,在三棱锥P-ABC中,∠PAC=∠BAC=90°,PA=PB,点D,F分别为BC,AB的中点.

(1)求证:直线DF∥平面PAC;

16.(本小题满分14分)已知函数f(x)=-(x+2)(x-m)(其中m>-2),g(x)=2x-2=0.

(1)若命题“log2g(x)≤1”是真命题,求x的取值范围;

(2)设命题p:∀x∈(1,+∞),f(x)<0或g(x)<0.若p是假命题,求m的取值范围.

(1)求f(x)的最小值h(a);

(2)是否存在实数m,同时满足以下条件:①m>n>3;② 当h(a)的定义域为[n,m]时，值域为[n2,m2];若存在,求出m,n的值;若不存在,说明理由.

18.(本小题满分15分)从旅游景点A到B有一条100公里的水路,某轮船公司开设一个观光项目.已知游轮每小时使用的燃料费用与速度的立方成正比例,其他费用为每小时3 240元,游轮最大时速为50 km/h.当游轮速度为10 km/h,燃料费用为每小时60元,若单程票价定为150元/人.

(1)一艘游轮单程以40 km/h航行,所载游客为180人,轮船公司获得的利润是多少?

(2)如果轮船公司要获取最大利润,游轮的速度为多少?

19.(本小题满分16分)函数f(x)=(ax2+x+2)ex(a>0),其中e是自然对数的底数.

(1)当a=2时,求f(x)的极值;

(2)若f(x)在[-2,2]上是单调增函数,求a的取值范围.

(1)求a的值;

(2)若函数g(x)=f(x)-b有两个不同的零点,求实数b的取值范围;

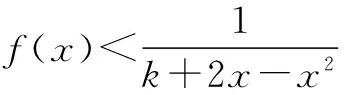
(2)求证:PF⊥AD.