揭示高考数学试题本质的若干策略

赵爱华　肖松柏

(新疆乌鲁木齐市教育研究中心,830000)　(新疆大学附属中学,830046)

揭示高考数学试题本质的若干策略

赵爱华肖松柏

(新疆乌鲁木齐市教育研究中心,830000)(新疆大学附属中学,830046)

数学高考考试大纲指出:数学科考试要考查对数学思想方法和数学本质的理解水平,要考查进入高等学校继续学习的潜能. 在中学数学教学中,借助题目,探寻其背后所蕴含的数学本质,是有助于学生达到这个要求的．

下面,我们从多角度来揭示高考数学试题的本质,以期抛砖引玉．

策略1换元凸显本质

换元法是化简求值的一种重要的方法,通过整体代换可以化繁为简,通过化“多元”为“一元”达到降低难度的目的．教学中要让学生清楚使用换元的条件,明白换元的注意事项,掌握换元的常用方法,引导学生运用换元法来揭示问题的本质．

例1(2011年浙江高考题)设x、y为实数,若4x2+y2+xy=1,则2x+y的最大值是______.

分析本题有很好的开放性,不同的视角就有不同的解法．学生最容易想到的常规方法应该是二元变一元,因此将2x+y看成一个变量t,消去y,得到一个关于x的含参数t的二次方程,利用二次方程有解时Δ≥0就可稳妥解决问题．

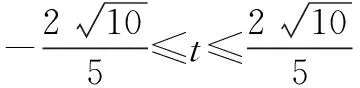
同类试题练习:

策略2数形结合观察本质

数形结合是高考要求的一种重要思想方法．我国著名数学家华罗庚曾说过:数形结合百般好,隔离分家万事休．通过“以形助数”或“以数解形”即可以使复杂问题简单化,抽象问题具体化,从而起到优化解题途径的目的．要想更好地使用数形结合法,要求学生必须掌握基本初等函数的图象和基本初等函数通过平移、伸缩等变换后的函数图象．

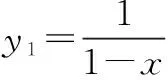
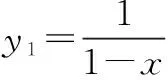
所以在(1,4)内函数y1与y2的图象有四个交点E、F、G、H；相应地,在(-2,1)内有四个交点A、B、C、D,且xA+xH=xB+xG=xC+xF=xD+xE=2,故所求的横坐标之和为8.

同类试题练习:

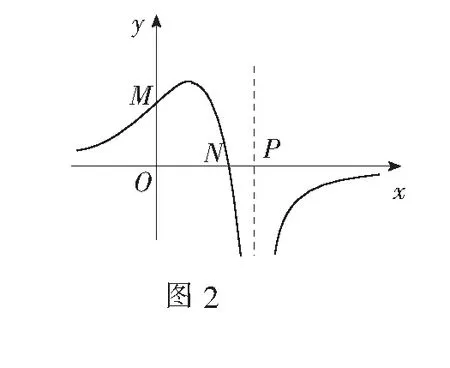
(A)a>0,b>0,c<0

(B)a<0,b>0,c>0

(C)a<0,b>0,c<0

(D)a<0,b<0,c<0

答案:C.

策略3结构反应本质

数学中大量的问题隐含着形的信息,因此,抓住所给数式结构的特征,联想有关的数学定义,挖掘出数式的几何意义,把数式问题转换到图形上来,常常能使问题获得形象、直观的解法.

分析分子中有分母的相同项时,分离时常数是常用技巧．剩余部分构成奇函数,题中的结构M+m提示你需要利用奇函数最大值与最小值之和为0这一本质．

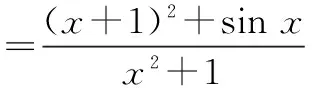
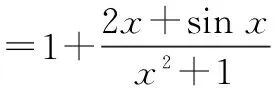
对奇函数来说,g(x)max+g(x)min=0,而f(x)max=1+g(x)max,f(x)min=1+g(x)min,所以f(x)max+f(x)min=2， 即M+m=2.

同类试题练习:

策略4概念蕴含本质

数学概念是数学基础知识的核心,是数学推理和论证的要素,是学好数学知识和培养数学能力的关键．新课标强调数学教学应当使学生对数学概念本质达到理性认识．在解决某些概念明显的题时，若回归概念就能找到解决问题的方法．

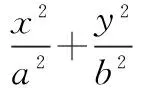
分析题设中有“焦点”、“面积”等信息,应该联想到焦点三角形这个概念,焦点三角形面积公式恰好提供了b2．本题用其他方法都有不同程度的运算,本质节约了运算和时间．

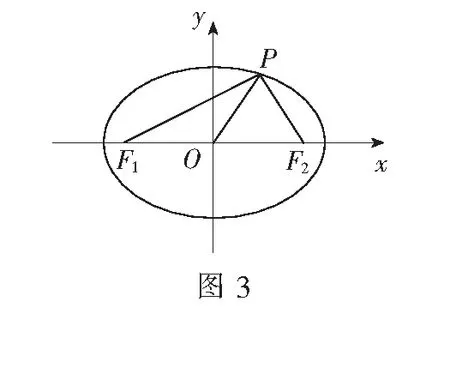
解如图3,根据题意得∆OPF2是正三角形,则OP=OF2=OF1, ∠POF2=∠OPF2=60°,∠OPF1=30°,因此∠F1PF2=30°+60°=90°.又椭圆焦点三角形的面积公式为

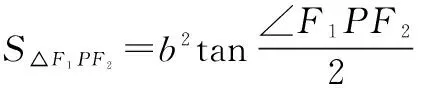
根据题意，得

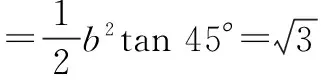
同类试题练习:

(2006年浙江高考题)函数f:{1,2,3}→{1,2,3}满足f(f(x))=f(x),则这样的函数个数共有()

(A)1个(B) 4个

(C) 8个(D) 10个

答案:D.

策略5运算决定本质

运算求解能力是课标要求的五大能力之一,也是高考要求的基本能力之一．每年都有考查学生计算能力的高考题．只要我们会根据概念、公式、法则进行数、式、方程的正确运算与变形,能分析条件,寻求与设计合理、简捷的运算途径,能根据要求对数据进行估算,并能进行近似计算,加点小心就可以解决问题．

例5已知函数f(x)=x(ex+ae-x)(x∈R)是偶函数,则a=______.

分析本题主要考查学生的计算能力,可以直接利用偶函数的定义f(-x)=f(x)求解,也可通过奇偶函数的性质求解,没有多大难度,只要按部就班计算即可．

解法1由f(-x)=f(x),得

x(-aex-e-x)=x(ex+ae-x)，

即(1+a)xe2x=0.

所以a+1=0，解得a=-1．

解法2由f(x)=x(ex+ae-x)是偶函数得g(x)=ex+ae-x是奇函数.又因为f(x)的定义域为R,所以g(0)=0,即g(0)=1+a=0,解得a=-1.

解法3由f(x)是偶函数,得

f(-1)=f(1).

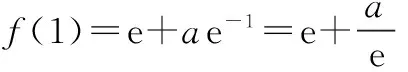
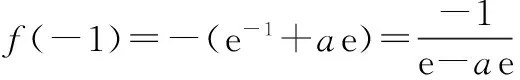
同类试题练习:

(2009年全国高考题)已知直线y=k(x+2)(k>0)与抛物线C:y2=8x相交A、B两点,F为C的焦点．若|FA|=2|FB|,则k=()

答案:D.

策略6变形找到本质

“变形”是数学中的重要基础,也是一项基本技能．是探索数学问题解答的一种有效方法,是开拓思路,发展智力,培养能力的途径之一．“变形”要变之有用,变之有规,变之有益．有些问题变形目标是明确的,比如函数单调性的证明、奇偶性的判定、三角函数、几何证明等目标都是明确的．

例6(2015年北京高考题)已知函数

(1)求f(x)的最小正周期;

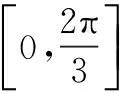
分析求解与三角函数性质有关的问题,一般方法是利用辅助角公式收缩成一个角的三角函数f(x)=Asin(ωx+φ)+B的形式,借助三角函数性质求解．因此本题目标是明确的,就看如何变形化成f(x)=Asin(ωx+φ)+B的形式．

∴f(x)的最小正周期

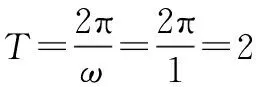
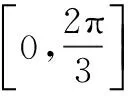
同类试题练习:

(A) 奇函数(B) 偶函数

(C) 既奇又偶函数(D) 非奇非偶函数

答案:A.