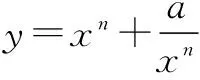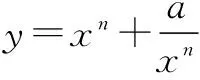谈谈函数能力型问题的类型及其解题策略

史立霞　秦　振

(山东省枣庄市第三中学西校，277100)

谈谈函数能力型问题的类型及其解题策略

史立霞秦振

(山东省枣庄市第三中学西校，277100)

本文介绍的函数能力型问题是指与解决实际问题的能力和数学创新能力的有关数学问题，这些问题能体现我们对问题的领悟过程．下面分类例说函数能力型问题常见题型及解题策略．

一、学习能力问题

学习新的数学知识的能力是指通过阅读、理解以前没有学过的新的数学知识,包括新的概念、定理、公式、法则和方法,并能应用它们作进一步的运算和推理,解决有关问题的能力．这类问题的解题策略是先阅读题目,理解所给的新定义、新概念、新运算,在新的情景中的意义,然后类比所学知识,转化为熟悉的知识解决．

例1对于定义域为D的函数y=f(x),如果存在区间[m,n]⊆D,同时满足:①f(x)在区间[m,n]内是单调函数;②x∈[m,n]时,f(x)的值域也是[m,n]，则称[m,n]是该函数的“和谐区间”．

(2)已知函数

(a∈R,a≠0)有“和谐区间”[m,n],当a变化时,求出n-m的最大值;

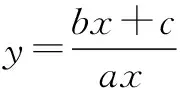
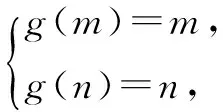
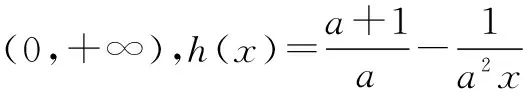
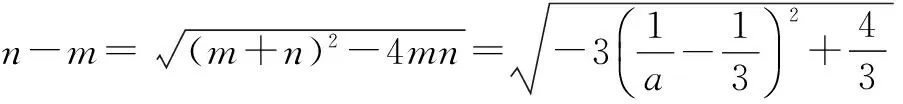
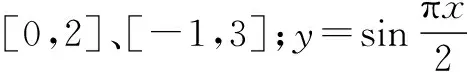
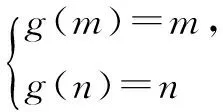
二、探究能力问题

这里的探究问题,是指命题中缺少一定的条件或未给出明确的结论,需要经过推断、补充并加以证明的问题．由于这类问题的知识覆盖面大,综合性强,方法灵活,再加上题意新颖,要求考生具有扎实的基础知识和较高的数学能力．解决这类问题需要运用学过的知识,通过观察、试验、联想、类比、演绎、归纳、分析、综合、猜想等手段,对问题进行探索和研究．

例2对于函数f1(x),f2(x),h(x),如果存在实数a,b,使得h(x)=a·f1(x)+b·f2(x),那么称h(x)为f1(x),f2(x)的生成函数．

(1)下面给出两组函数,h(x)是否为f1(x),f2(x)的生成函数?并说明理由.

第二组:f1(x)=x2+x,f2(x)=x2+x+1,h(x)=x2-x+1.

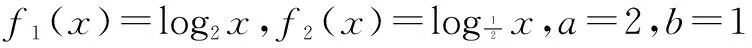
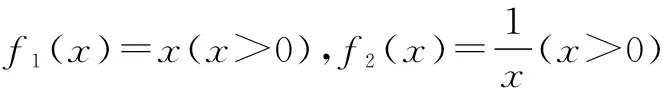
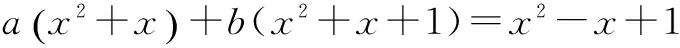
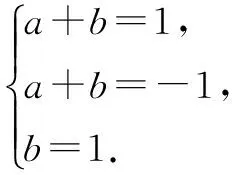
该方程组无解,故h(x)不是f1(x),f2(x)的生成函数．

设s=log2x,则s∈[1,2]．易知y=-3s2-2s,在s=1时取最大值-5,所以实数t的取值范围是t∈(-∞,-5)．

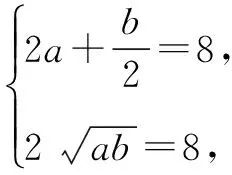
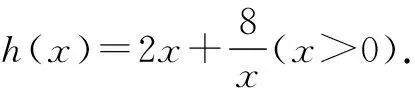
假设存在最大的常数m,使h(x1)h(x2)≥m恒成立．设u=h(x1)h(x2),则

令t=x1x2,则

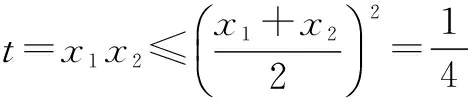
评注数学探究题涉及的数学知识较多,解题过程较复杂,技巧性强,因此,要求我们要合情合理地分析,把直觉发现与逻辑推理相结合,更应该注重数学思想方法的综合运用．解此类问题的方法是:分析问题的特征——假设存在——演绎推理——得出结论．

三、应用能力问题

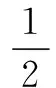
设用x单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留农药量之比为函数f(x)．

(1)试规定f(0)的值,并解释其实际意义;

(2)试根据实验写出的函数f(x)应该满足的条件和具有的性质;

解(1)根据题意,规定f(0)=1表示没有用水清洗时,蔬菜上的农药量将保持原样．

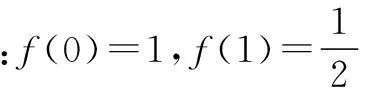
(3)设仅清洗一次,残留的农药量为

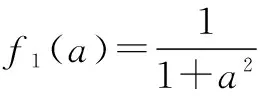
清洗两次后,残留的农药量为

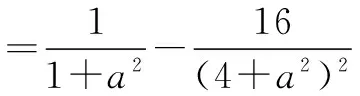
于是有如下三种情形：

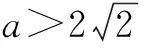
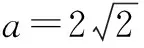
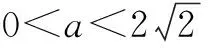
在情形① 时,清洗两次后残留的农药量较少;情形② 时两种清洗方法具有相同的效果;情形③ 时,一次清洗残留的农药量较少．

评注用数学知识解决实际问题,在数学学习中越来越体现出其重要地位,因此，要通过练习逐步掌握用所学数学知识解决生活中遇到的问题的方法,提高生活质量和数学素养．

四、创新能力问题

(2)设0

评注问题(3)推广时，对n奇偶性应该考虑问题的不同之处,由“不同之处”适当“修正”对应的结果．利用类比推理可以推测未知,发现新结论,寻找解决问题的思路和方法．

能力型问题旨在考察学生的阅读、分析、归纳、概括和自学能力．因此在解题时,必须注意:阅读定义、定理和公式时要理解其中的因果关系;阅读解题过程时,在看懂过程的同时要注重内蕴的数学思想方法;在方法模拟问题中,要注意迁移发展,探索创新．