聚焦圆锥曲线的热点问题

佘媛媛　张世林

(湖北省巴东一中，444300)

○高考之窗○

聚焦圆锥曲线的热点问题

佘媛媛张世林

(湖北省巴东一中，444300)

圆锥曲线的热点问题往往是试卷的压轴题之一.一般以直线与圆锥曲线、圆与圆锥曲线为载体,考查弦长、定点、定值、最值、范围问题或探索性问题.能力要求高,综合性强．本文就圆锥曲线的三类热点问题给出常见的应对策略，供大家参考.

一、圆锥曲线中的范围、最值问题

圆锥曲线的最值与范围问题的常见解法:① 几何法:若题目的条件和结论能明显体现几何特征和意义,则考虑利用图形性质来解决;② 代数法:若题目的条件和结论能体现一种明确的函数关系,则可首先建立起目标函数,再求这个函数的最值．

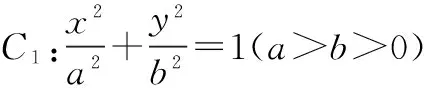
(1)求椭圆C1的方程;

(2)求∆ABD的面积取最大值时直线l1的方程.

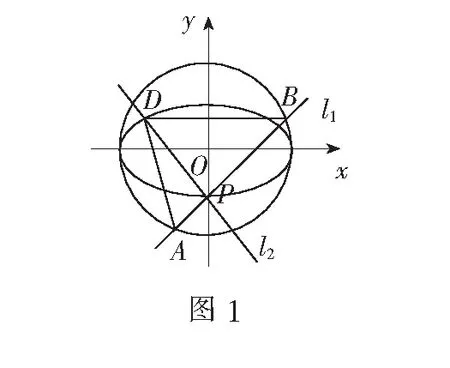
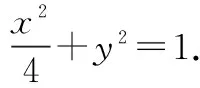
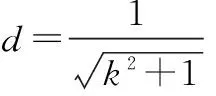
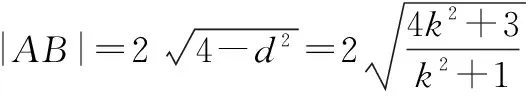
又l1⊥l2,故l2的方程为x+ky+k=0.

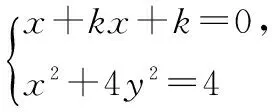
(4+k2)x2+8kx=0,

设∆ABD的面积为S,则

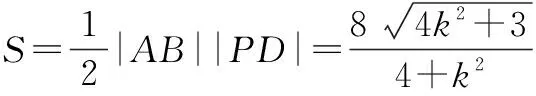
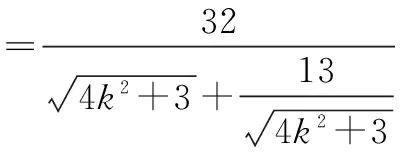
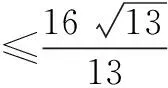
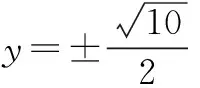
评注本题从图形的几何性质出发，将|AB|及|PD|表示为k的函数，方便了目标函数的建立，轻松解决了问题.

(1)求椭圆C的方程;

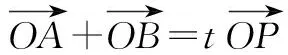
(2)由题意知直线AB的斜率k存在,故可设直线AB的方程为y=k(x-2),A(x1,y1),B(x2,y2),P(x,y).

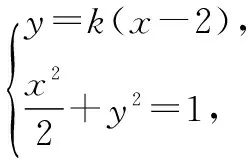
(1+2k2)x2-8k2x+8k2-2=0.

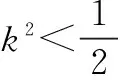
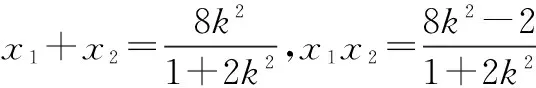
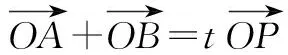
∴(x1+x2,y1+y2)=t(x,y),

∵点P在椭圆C上,

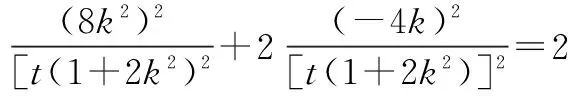
∴16k2=t2(1+2k2).

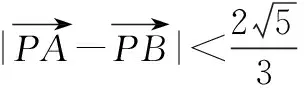
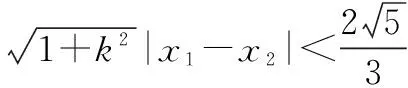
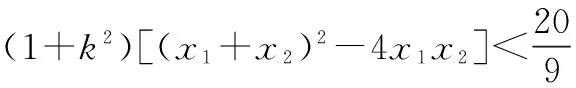
∵16k2=t2(1+2k2),

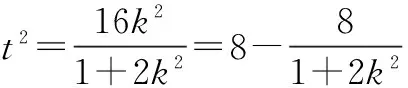
∴实数t的取值范围为

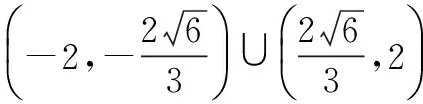
二、圆锥曲线中的定值、定点问题

定值、定点问题必然是在变化中所表现出来的不变的量,处理时直接推理求出定值,也可先通过特定位置猜测结论后进行一般性证明,对于客观题,通过特殊值法探求定点、定值能达到事半功倍的效果．

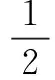
(1)求椭圆C的方程;

(2)如图2，已知点P(2,3),Q(2,-3)在椭圆上,点A、B是椭圆上不同的两个动点,且满足∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.

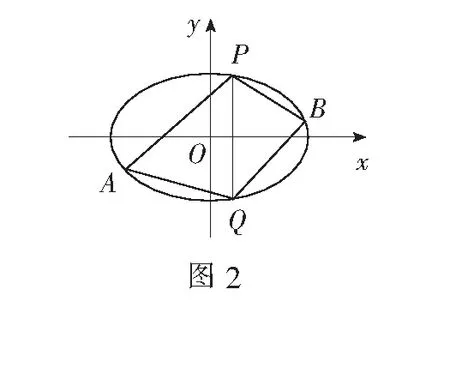
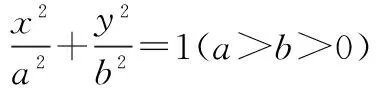
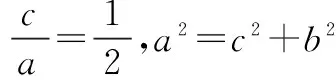
(2)当∠APQ=∠BPQ时,PA,PB的斜率之和为0.设直线PA的斜率为k,则PB的斜率为-k,PA:y-3=k(x-2).

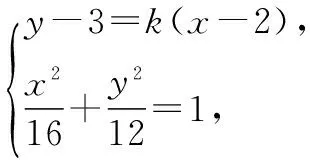
(3+4k2)x2+8(3-2k)kx+

4(3-2k)2-48=0,

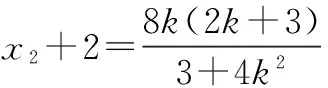
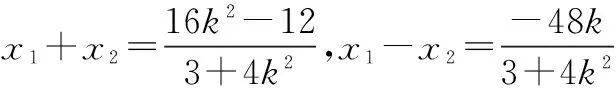
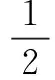
评注定值问题就是在运动变化中寻找不变量的问题,本题基本思想是使用参数表示AB的斜率kAB,证明kAB与参数无关.在这类试题中选择消元的方向是非常关键的.

(1)求椭圆E的方程;

∴a2+b2=7；

①

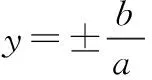
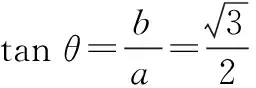
②

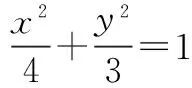
(2)在(1)的条件下,当直线PQ的斜率k存在时,设直线PQ的方程为y=kx+m.

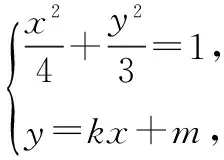
(3+4k2)x2+8kmx+4m2-12=0.

设P(x1,y1),Q(x2,y2),则

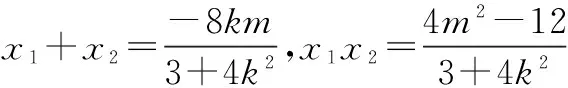
又A(-2,0),由题意知

(x1+2)(x2+2)+4y1y2=0,

且x1x2≠-2,x1x2+2(x1+x2)+4

+4(kx1+m)(kx2+m)=(1+4k2)x1x2

+(2+4km)(x1+x2)+4m2+4=0,

即m2-km-2k2=0，

(m-2k)(m+k)=0，

∴m=2k或m=-k.

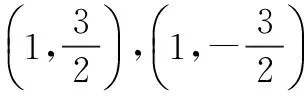
综上,直线PQ恒过定点(1,0).

三、圆锥曲线中的探索性问题

探索性问题主要是存在性问题.求解时一般先假设存在,然后进行合理的推理论证.若得到的结论符合情理则假设成立,若得到矛盾的结论则假设不成立．

例5如图3,抛物线C:y2=2px的焦点为F,抛物线上一定点Q(1,2).

(1)求抛物线C的方程及准线l的方程；

(2)过焦点F的直线(不经过Q点)与抛物线交于A,B两点,与准线l交于点M,记QA,QB,QM的斜率分别为k1,k2,k3,问是否存在常数λ,使得k1+k2=λk3成立？若存在λ,求出λ的值;若不存在,说明理由.

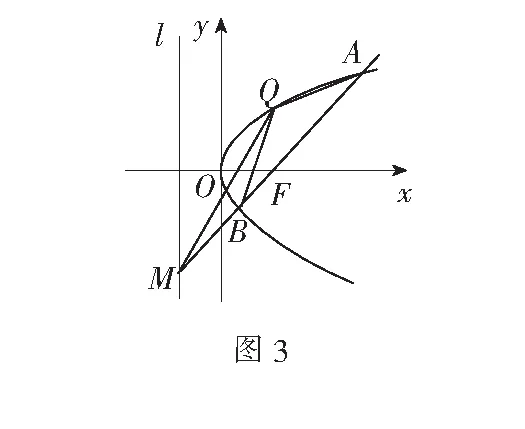
解(1)把Q(1,2)代入y2=2px,得2p=4,所以抛物线方程为y2=4x,准线l的方程为x=-1.

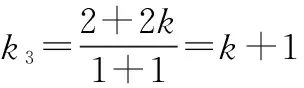
把直线AB的方程y=k(x-1),代入抛物线方程y2=4x,并整理,可得k2x2-2(k2+2)x+k2=0.设A(x1,y1),B(x2,y2),则x1+x2=

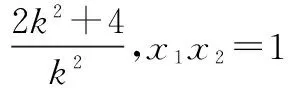
=2(k+1),

即存在常数λ=2,使得k1+k2=2k3成立.

评注解析几何中的探索性问题,从类型上看,主要是存在类型的相关题型.解决问题的一般策略是先假设结论成立,然后进行演绎推理或导出矛盾,即可否定假设或推出合理结论,验证后肯定结论.对于“存在”或“不存在”的问题,直接用条件证明或采用反证法证明.解答时,不但需要熟练掌握圆锥曲线的概念、性质、方程及不等式、判别式等知识,还要具备较强的审题能力、逻辑思维能力以及运用数形结合的思想分析问题和解决问题的能力.