巧用转化法解最值问题

◇　山东　王　芳

巧用转化法解最值问题

◇山东王芳

最值问题一直是近些年高考的重点和难点,也是必考内容．对于一些结构复杂的问题,利用转化法可以有效地简化题目结构、化抽象为具体、化繁为简．本文将结合实例,对转化法在最值问题中的应用进行探究,帮助学生理清解题思路．

1三角代换转化

可用三角换元求解的题目一般具有比较明显的特征,若能发现规律,便可选对方法,进而顺利求解．

从S=x2+y2的形式出发提问学生：高中有哪些类似形式的公式,学生不难联想到sin2x+cos2x=1．于是采用三角换元.

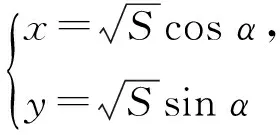
对于三角换元问题,最重要、也是学生最容易犯错的地方就是对代换后的式子取值范围的判定．

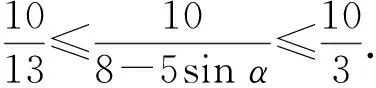
2数与形的转化

数形结合不仅是一种解题方法，更是一种有效联系几何与代数的桥梁.通过数形结合思想的使用，学生可以将函数问题与几何图形相联系，利用图象的几何意义进行函数最值求解.但这样的思路往往需要学生具有很强的逻辑思维能力，能够清晰有效地使用图形的几何意义进行解题.

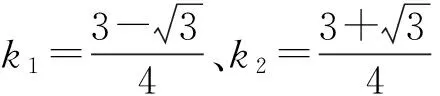
上述所求得的最值即是本题函数的最值．

3整体与局部的转化

在研究和解决数学问题时，若问题所给对象不能按统一的思维和方法解决，可根据实际情况，把所要研究的对象分成几类来讨论，使每一类问题都变得较为简单、具体，便于操作.“化整为零，集零为整”是它的本质.分类讨论的原则是：标准统一，对象确定，不重不漏，不越级讨论.

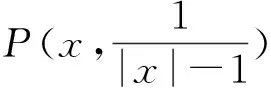
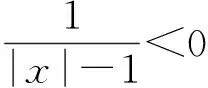
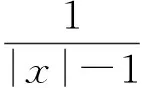
要想得到|CP|的最值,可设t=x-1(t>0),即

从上式可得当u=-1时,

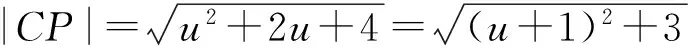
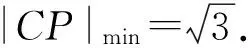
综上可知,囧圆面积取得的最小值为3π．

4主元与辅元的转化

对于涉及多个变量的问题中，可将某个变量看作主要变量，其他变量看作参数，从而使问题得到解决.

x2+y2+z2=m可得

(7-2y+3z)2+y2+z2=m.

将y看作主元，整理得

5y2-(12z+28)y+10z2+42z+49-m=0.

因为y存在，所以Δ1≥0,即

(12z+28)2-20(10z2+42z+49-m)≥0,

即

14z2+42z+49-5m≤0.

再将z看作主元，因为z存在，所以Δ2≥0，即

422-56(49-5m)≥0,

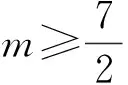
除了上述几种转化方法以外，还有特殊与一般的转化、正与反的转化、抽象与具体的转化等，望同学们在学习中不断归纳总结，以提升自己分析问题解决问题的能力．

(作者单位：山东省荣成市第二中学)