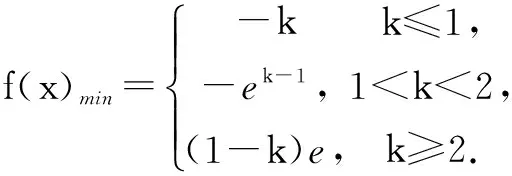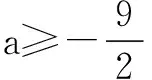一类区间上二次函数最值问题的求解与推广

2016-06-12吴志鹏

高中数学教与学 2016年8期

关键词：极小值极大值增函数

吴志鹏

(福建省德化第一中学，362500)

一类区间上二次函数最值问题的求解与推广

吴志鹏

(福建省德化第一中学，362500)

一、与参数有关的区间上二次函数最值问题

关于二次函数f(x)=ax2+bx+c(a≠0)在[m,n]上的最值问题,解答时可通过置放二次函数图象的对称轴或所给区间,截取相应区间的图象获得最值,主要类型有以下三种:

1.区间确定,对称轴位置待定

例1求函数f(x)=2x2-2ax+1在[-1,1]上的最小值.

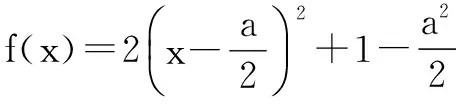
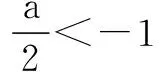
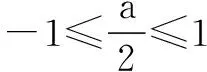
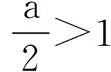
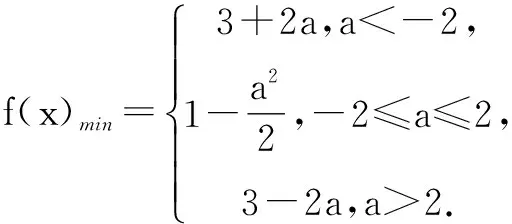
2.对称轴位置确定,区间待定

例2求函数f(x)=x2-2x+3在区间[t,t+1]上的最小值.

解由f(x)=(x-1)2+2知二次函数对称轴为确定直线x=1,而区间[t,t+1]因含参数t而不确定.此时可将区间置于对称轴的左右两侧或将对称轴置于区间内部三种情况,作图观察获得结论.

当t+1<1,即t<0时,函数y=f(x)在[t,t+1]上为减函数,f(x)min=f(t+1)=t2+2；

当t≤1≤t+1,即0≤t≤1时, f(x)min=f(1)=2；

当t>1时,函数y=f(x)在[t,t+1]上为增函数,f(x)min=f(t)=t2-2t+3.

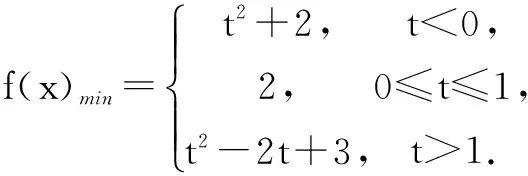
3.对称轴、区间均确定,函数图象开口方向待定

例3已知二次函数f(x)=ax2+2ax+3在[-3,2]上的最大值为5,求实数a的值.

解f(x)=a(x+1)2+3-a.

此时，二次函数图象的对称轴为定直线x=-1,区间[-3,2]也确定，但函数二次项系数a(a≠0)待定,此时可按a>0(开口向上)或a<0(开口向下)两类情况进行讨论(如图1).

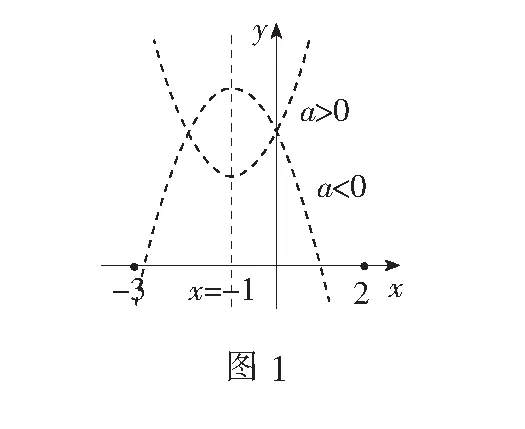
当a>0时,函数图象开口向上,则f(x)max=f(2)=8a+3=5,解得

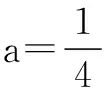
当a<0时,函数图象的开口向下,则f(x)max=f(-1)=3-a=5,解得a=-2.

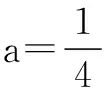
二、迁移推广

由二次函数的图象可知函数在对称轴处取得极值,开口向上时为极小值,开口向下时为极大值,极值点两侧图象的单调性相反且对称.解决与参数相关二次函数最值问题,我们可以根据以上三种情况进行分析解答.对于极值点左右两侧图象具有非对称关系的函数，我们也可以迁移二次函数在某区间求最值方法解决问题.两种解决方案有着异曲同工之妙.

1.区间确定,极值点位置待定

例4(2011年北京高考题)已知f(x)=(x-k)ex.

(1)求f(x)的单调区间;

(2)求f(x)在区间[0,1]的最小值.

解(1)∵ f ′(x)=(x-k+1)ex,令f ′(x)=0,得x=k-1.

当xk-1时,f ′(x)>0，∴f(x)的递减区间为(-∞,k-1),递增区间为(k-1,+∞).

(2)由(1)知当x=k-1时,f(x)取得极小值也是最小值.

由k为参数,知极小值x=k-1的位置待定,而区间[0,1]确定,此时极小值点的位置可按置于区间[0,1]的左、右侧、区间内三种情况讨论.

当k-1≤0,即k≤1时,f(x)在[0,1]上为增函数,f(x)min=f(0)=-k；

当0

当k-1≥1,即k≥2时,f(x)在[0,1]上为减函数,f(x)min=f(1)=(1-k)e.