基于平面八杆机构的书架桌设计与研究

戴宁

（江苏建筑职业技术学院，江苏徐州221116）

基于平面八杆机构的书架桌设计与研究

戴宁

（江苏建筑职业技术学院，江苏徐州221116）

书架是长期陈列书籍的工具，桌子是灵活取放物品的工具，将书架与桌子的属性组合起来，平时为二层书架，当需要就地学习时，将书架后面四块挡板中的两块翻转上来，桌面出现了，成为了临时学习的桌子。挡板到桌面以及再返回的过程由平面八杆机构实现，建立了平面八杆机构的设计方程，利用设计实例表明了设计方法的简明与正确。

书架桌；平面八杆机构；设计与研究

桌子在结构、色彩与功能方面得到持续的研究，其中折叠桌倍受关注，通过可变结构获得不同的功能、占据不同的空间。书架也在不断的改进之中，通过改变现有书架的结构让读者获得新鲜感的书架，具有查找出乱架图书以及相对应的正确架位的书架，以及可升降书架等。本文将书架与桌子组合起来，通过左右各一个平面八杆机构，得到了平时为书架，用书时为桌子的书架桌。

具有多层隔板的书架一直是图书馆陈列书籍的工具，圆桌与方桌一直是人们学习与生活的工具，长期以来书架与桌子相对独立存在，这既体现了使用上的灵活性，也使得各自的设计与制造互不相关，设计上各自别具一格，制造上各自精益求精，使用上各取所需。现在的图书馆将书架与桌子分离放置，既具有空间布局的美感，也具有空间利用率较高的优点，这使得图书馆成为藏书的宝库与博览群书的宝地。美中不足的是，图书馆的格局过于单调，缺乏激发读者创新的物品。为此，将书架与桌子的属性组合起来，平时为一个两层的书架，当需要就地学习时，将书架后面四块挡板中的两块翻转上来，桌面出现了，这样就成为了一个临时学习的桌子。两块挡板到桌面以及再返回的过程由左右各一个平面八杆机构实现，采用代数方法设计了该平面八杆机构，设计实例展示了设计过程。

1 平面八杆机构的尺寸设计

两层书架桌的机构左视图如图1所示，作为书架时的高度为h0、宽度为b；作为书桌时的高度为h1、宽度为b0。

图1 书架桌变换的平面八杆机构

桌面由两块矩形板组成，每一块桌面的宽度为h8、长度为L。两块桌面板也是书架的两块后挡板。

每一块桌面沿宽度方向两个转动副之间的距离为h6，每一块桌面两个转动副沿宽度方向到各自端面的距离为h5，上后挡板与下后挡板之间的距离为h7，下后挡板的下铰链D1到地面的距离为h9，后挡板的外侧到D1点的距离为h2，桌面即后挡板的厚度为h3，桌面下铰链座外圆弧到桌面顶面的距离为h4=h2+4，b1是O3、O4点的水平坐标，b2是O2点的水平坐标，b3是O1点的水平坐标。

在图1中，O1ABO2组成上后挡板到前桌面相互变换的第一个双摇杆机构，而O3CDO4组成下后挡板到后桌面相互变换的第二个双摇杆机构，O2EFO4组成前两个双摇杆机构的联动双摇杆机构。

如图1所示的坐标系xD1y中，D1点的坐标为xD1=0、yD1=0，C1点的坐标为xC1=0、yC1= h6，B1点的坐标为xB1=0、yB1=h6+2h5+h7，A1点的坐标为xA1=0、yA1=2h6+2h5+h7，D2点的坐标为xD2=-h2+h3+h5、yD2=2h6+3h5+ h7+h4-h2，C2点的坐标为xC2=-h2+h3+h5+h6、yC2=yD2，B2点的坐标为xB2= -h2+h3+ 3h5+h6、yB2=yD2，A2点的坐标为xA2= -h2+ h3+3h5+2h6、yA2=yD2。

对于O3CDO4组成的第二个双摇杆机构，当O4D从O4D1摆到O4D2时，D1、D2中点的坐标分别为 xD12= (xD1+xD2)/2、yD12= (yD1+yD2)/2，直线D1D2的斜率为kD= (yD2-yD1)/(xD2- xD1)，直线D1D2中垂线的方程为：

令x=xO4=b1，得y=yO4为：

C1、C2中点的坐标分别为xC12= (xC1+xC2)/ 2、yC12= (yC1+yC2)/2，直线C1C2的斜率kC= (yC2-yC1)/(xC2-xC1)，直线C1C2中垂线方程为：

令x=xO3=b1，得y=yO3为：

于是，摇杆O4D的杆长l5、摇杆O3C的杆长l7、机架O3O4的杆长l41分别为：

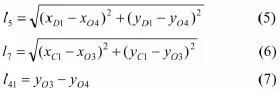
摇杆O4D的摆角b、摇杆O3C的摆角b分别为:

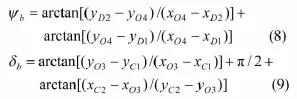
对于O1ABO2组成的第一个双摇杆机构，B1、B2中点的坐标分别为xB12= (xB1+xB2)/2、yB12= (yB1+yB2)/2，直线B1B2的斜率kB= (yB2-yB1)/(xB2-xB1)，直线B1B2中垂线的方程为：

令x=xO2=b2，得y=yO2为：

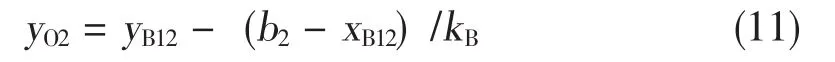
A1、A2中点的坐标分别为xA12= (xA1+xA2)/ 2、yA12= (yA1+yA2)/2，直线A1A2的斜率kA= (yA2-yA1)/(xA2-xA1)，直线A1A2中垂线方程为:

令x=xO1=b3，得y=yO1为：

于是，摇杆O2B的杆长l1、摇杆O1A的杆长l3、机架O2O3的杆长l42、O1O2的杆长l43分别为:

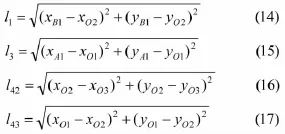
摇杆O2B关于O2的摆角b、摇杆O1A关于O1的摆角b分别为:

O4D1关于 -y轴的初相位角0、O2B1关于-y轴的初相位角0分别为:

对于O2EFO4组成的联动双摇杆机构，如图2所示，设摇杆O2B上O2E的杆长为l11，摇杆O4D上O4F的杆长为l51，连杆EF的杆长为l8，x24=xO2-xO4，y24=yO2-yO4，则联动双摇杆机构在任意位置的尺寸关系为:

图2 平面四杆联动机构的极限位置

引入系数k1=1/l11，k2=-1/l51，k3= (x224+y224+l211+l251-l28)/(2l51·l11)，得设计方程为:

取三个位置进行设计，ψ=0、φ=0；ψ= 0.5ψb、φ=xs·φb；ψ=ψb、φ=φb，xs为位置系数，得线性设计方程组，由此解得k1、k2与k3，于是，l11、l51、l8分别为:

2 平面八杆机构的设计实例

已知b0=400 mm，b=330 mm，b1=160 mm，b2=200 mm，b3=195 mm，h0=800 mm，h1=828 mm，h2=24 mm，h3=19 mm，h4=28 mm，h5=20 mm，l2=l6=h6=160 mm，h7= 136 mm，h8=200 mm，h9=284 mm，L=1 200 mm，xs=0.4。由以上公式经编程计算得设计参数的数值如表1所示。

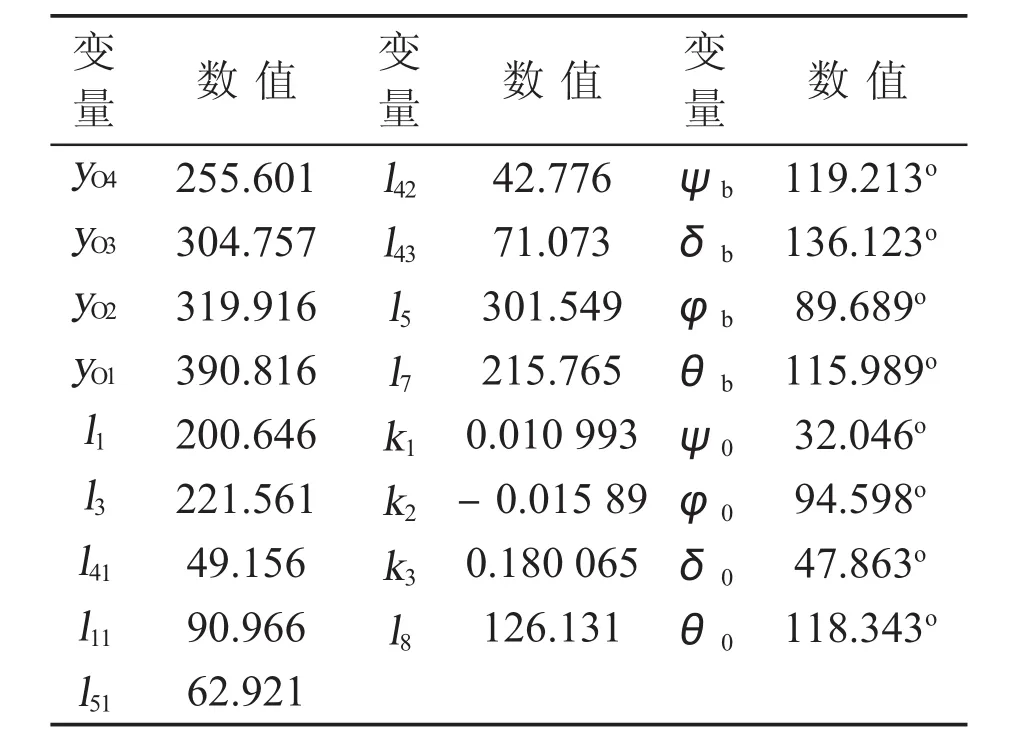
表1 平面八杆机构的设计参数 （mm）

书架桌的三维结构如图3、图4所示，左端的平面八杆机构安装在左侧支板1与上左隔板9、下左隔板8之间的空间内，左定位销轴10用于定位图1中的O1A杆，右端的平面八杆机构安装在右侧支板与上.右隔板、下右隔板之间的空间内。

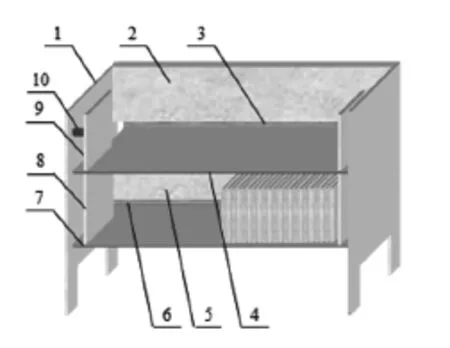
图3 书架桌处于书架状态

图4 书架桌处于书桌状态

3 结论

将三个双摇杆机构有机组合，其中两个连杆外连两块桌面板、另一个连杆实现联动，创新设计出了基于平面八杆机构的书架桌。该设计的出现既丰富了书架的功能，也方便了读者就地学习，同时还可以启发读者创新的激情，引导读者以问题为起点、以知识结构为支撑、以筛选方法为抓手，开展创新实践。

[1]张鸿锋,梁斌梦,卢结铃,等.创意平板折叠桌的设计[J].汕头大学学报(自然科学版),2015(3):31-42.

[2]刘雅倩,朱家明,曾淑娴.创意平板折叠桌的设计及优化模型[J].赤峰学院学报(自然科学版),2015(9):40-42.

[3]赵心愿,玄海燕,李玥,等.圆面折叠桌的动态模型[J].兰州文理学院学报(自然科学版),2015(3):25-28+41.

[4]贺孝梅,金旦亮,邱福喜,等.基于UCD的高校图书馆“I”形书架改良设计研[J].包装工程,2014(22):110-113+121.

[5]韩亮,郎筠.基于RFID图书馆智能书架设计实例[J].现代情报,2013(11):142-146.

[6]杨达毅,赵旭,祖慧鹏.一种新型可升降书架[J].科技视野, 2013(34):189-191.

[7]戴宁.一种书架桌:中国,201510077716.6[P].2015-2-15.

[8]王洪欣,戴宁.机械原理课程上机与设计[M].南京:东南大学出版社,2007.

［责任编辑：刘 月］

Design and Study on Bookshelf and Book Table Based on Planar Eight-bar Mechanism

DAI Ning
(Jiangsu Vocational Institute of Architectural Technology,Xuzhou 221116,China)

Bookshelf is a long-term display of books,and table has been an implement taken out and placed articles flexibly.In this paper,attribute of bookshelf and that of table are combined,in normal times it is a twostored bookshelf,when one needs study on the spot,two baffles of four baffles at the back of bookshelf are overturned up,the top of a table appears,and it turns bookshelf into table used as study temporarily.Process from two baffles to the top of a table and returned to the starting point is realized by a planar eight-bar mechanism and its design equation is set up.A design example demonstrates the conciseness and exactness of the design method.

bookshelf table;planar eight-bar mechanism;design

TH112.1

A

2095-5928（2016）05-39-04

2016-06-05

戴宁 (1970-)，女，安徽无为人，馆员，硕士，研究方向：资源建设与管理。

10.16850/j.cnki.21-1590/g4.2016.05.012