一种铰链四杆机构仿真教学课件的开发
2021-03-17费冬青
费冬青
(上海开放大学闵行二分校 机械电子工程专业, 上海 200240)
0 引言
在铰链四杆机构的教学过程中,许多内容需要借助于图形才能讲解清楚;但若使用静态的图形,学生理解起来还存在一定困难;目前,新的多媒体教学手段层出不穷,若要开发一些订制的课件,条件是具备的;通过查阅知网平台,未发现有类似的文献。所以完成这篇关于铰链四杆机构仿真教学课件开发的文章,具有一定的创新意义。
1 铰链四杆机构定义
四个构件都用转动副连接的四杆机构,称为铰链四杆机构[1],如图1所示。
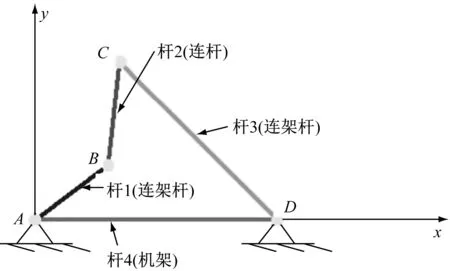
图1 铰链四杆机构示意图
其中,固定不动的杆4称为机架,与机架直接相连的杆1和杆3称为连架杆,在两连架杆中,能做整周转动的连架杆称为曲柄,不能做整周转动的连架杆称为摇杆,与机架不相连的杆2称为连杆。
2 求解从动杆位置
铰链四杆机构封闭矢量图,如图2所示。
AB为原动杆,CD为从动杆。求解从动杆位置就是在已知θ1的条件下,求θ3。由图2所示封闭矢量图,如式(1)。
(1)
由式(1)得式(2)。
lAB·cos(θ1)+i·lAB·sin(θ1)+lBC·cos(θ2)+i·lBC·sin(θ2)=
lAD+lDC·cos(θ3)+i·lDC·sin(θ3)
(2)
由式(2)得式(3)。
(3)
将式(3)消去θ2,如式(4)。

(2·lAD·lDC-2·lDC·lAB·cos(θ1))·cos(θ3)-
2·lDC·lAB·sin(θ1)·sin(θ3)
(4)
在式(4)中,设
A=2·lDC·lAB·sin(θ1)
B=2·lDC·lAB·cos(θ1)-2·lAD·lDC
得式(5)。
(5)
则上式变为式(6)。
C+Bcos(θ3)+Asin(θ3)=0
(6)
将


(7)
整理后,如式(8)。
(C-B)·x2+2·A·x+C+B=0
(8)
解这个一元二次方程,如式(9)。

(9)
则得式(10)、式(11)。
(10)
(11)

3 铰链四杆机构类型的判别[2]
如前述图1所示,当l杆1=l杆3并且l杆2=l杆4时,为平行四边形机构,平行四边形机构按主动杆与从动杆转向是否相同,还分为正平行四边形机构与反平行四边形机构。
当最短杆长度与最长杆长度之和,小于或等于其他两杆长度之和时。
(1) 若最短构件为连架杆,则该机构一定是曲柄摇杆机构。
(2) 若最短构件为机架,则该机构一定是双曲柄机构。
(3) 若最短构件为连杆,则该机构一定是双摇杆机构。
当最短杆长度与最长杆长度之和,大于其他两杆长度之和时,则该机构必为双摇杆机构。
4 铰链四杆机构仿真教学课件设计
4.1 计算从动杆角度
k = 0
For j = 0 To 360 '从动杆角度清零
从动杆角度(j) = 0
Next j
If ltype = 1 Then '曲柄摇杆,1杆为曲柄
For j = 0 To 359
i = j * pi / 180
A = 2 * 杆长(1) * 杆长(3) * Sin(i)
B = 2 * 杆长(3) * (杆长(1) * Cos(i) - 杆长(4))
C = 杆长(2) ^ 2- 杆长(1) ^ 2- 杆长(3) ^ 2- 杆长(4) ^ 2 + 2 * 杆长(1) * 杆长(4) * Cos(i)
If (A ^ 2 + B ^ 2- C ^ 2) >= 0 Then
原动杆角度(k) = i
atn3 = Atn((A- (Sqr(A ^ 2 + B ^ 2- C ^ 2))) / (B- C))
从动杆角度(k) = 2 * atn3
k = k + 1
End If
纵观2007-2016十年来中国婴幼儿配方乳粉进口贸易的发展,本文从规模、来源国和进口价格三个方面分析其贸易特征。
Next j
End If
以上程序中,将原动件以一度为步进值旋转一圈共360度,然后由式(5)确定A、B与C,由式(10)计算θ3/2,然后得到从动杆角度θ3。
4.2 绘制机构动态图
动画演示窗口.DrawWidth = 4
a1 = 原动杆角度(g)
a3 = 从动杆角度(g)
x1 = 杆长(1) * rr * Cos(a1)
y1 = 杆长(1) * rr * Sin(a1)
x3 = 杆长(4) * rr + 杆长(3) * rr * Cos(a3)
y3 = 杆长(3) * rr * Sin(a3)
动画演示窗口.Line (0, 0)-(x1, y1), vbBlue
动画演示窗口.Line (x1, y1)-(x3, y3), vbRed
动画演示窗口.Line (x3, y3)-(杆长(4) * rr, 0), vbGreen
动画演示窗口.Line (0, 0)-(杆长(4) * rr, 0), vbMagenta
动画演示窗口.FillStyle = 0
动画演示窗口.FillColor = vbYellow
动画演示窗口.Circle (杆长(4) * rr, 0), 0.5, vbYellow
动画演示窗口.Circle (0, 0), 0.5, vbYellow
动画演示窗口.Circle (x1, y1), 0.5, vbYellow
动画演示窗口.Circle (x3, y3), 0.5, vbYellow
上面程序中,rr为尺寸调整因子。该段代码为绘图子程序,在时间控件的事件中调用,调用时带入原动杆角度数组与从动杆角度数组。
4.3 课件演示
本课件可以显示平行四边形机构、曲柄摇杆机构(1杆为曲柄)、曲柄摇杆机构(3杆为曲柄)、双曲柄机构与双摇杆机构共五种机构的动态运行图。其中,平行四边形机构、曲柄摇杆机构(3杆为曲柄)与双摇杆机构这三种机构在编程上有特殊点,所以下面重点介绍一下。
4.3.1 平行四边形机构
平行四边形机构可以分别演示正平行四边形机构与反平行四边形机构。反平行四边形机构,如图3所示。
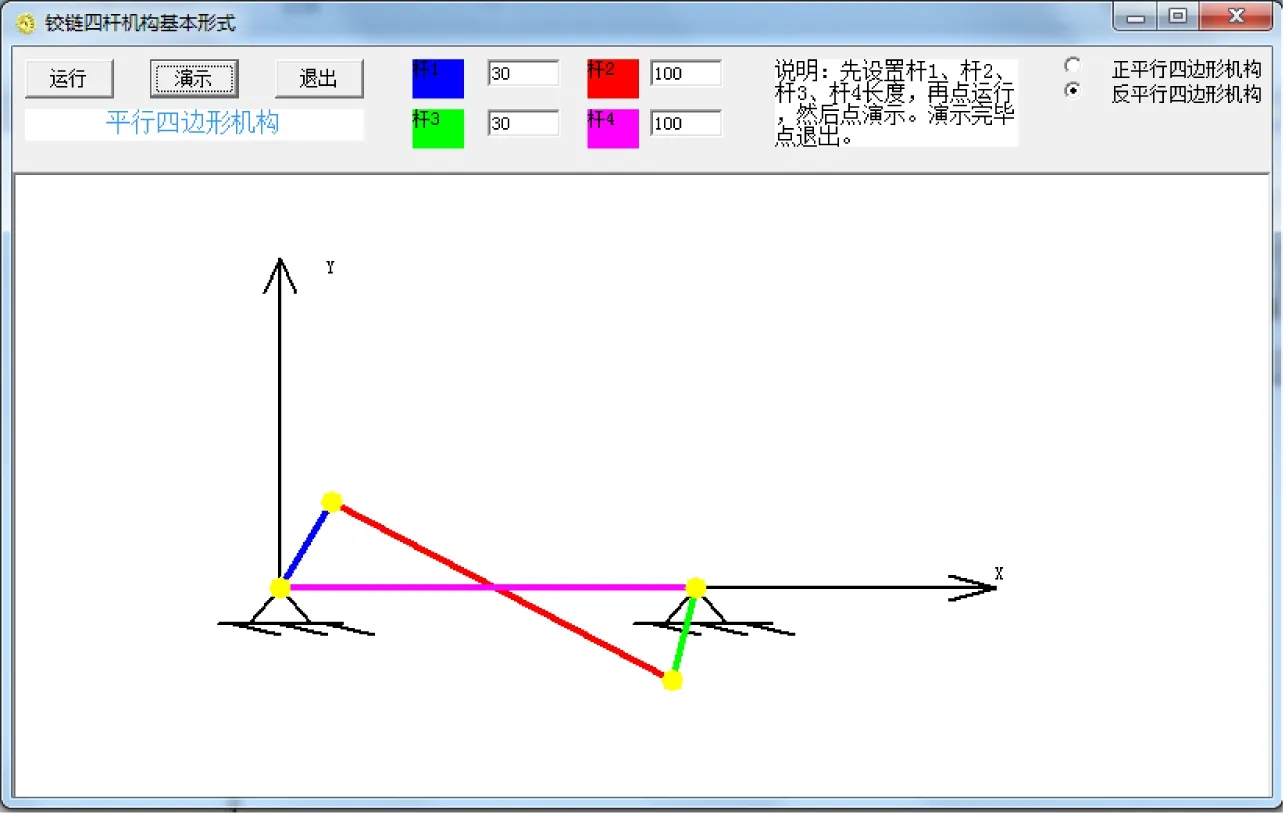
图3 反平行四边形机构
根据反平行四边形机构的运动连续性,在原动件的角度θ1在0°-180°变化时,θ3计算公式里面的∓号取正号;在原动件的角度θ1在181°-359°变化时,θ3计算公式里面的∓号取负号;正平行四边形机构则正好相反,在原动件的角度θ1在0°-180°变化时,θ3计算公式里面的∓号取负号;在原动件的角度θ1在181°-359°变化时,θ3计算式里面的∓号取正号。
反平行四边形机构计算θ2/2的代码如下。
If Option2.Value = True Then
If j <= 180 Then
atn3 = Atn((A + (Sqr(A ^ 2 + B ^ 2- C ^ 2))) / (B- C))
End If
If j > 180 Then
atn3 = Atn((A- (Sqr(A ^ 2 + B ^ 2- C ^ 2))) / (B- C))
End If
End If
4.3.2 曲柄摇杆机构(3杆为曲柄)
曲柄摇杆机构(3杆为曲柄),如图4所示。
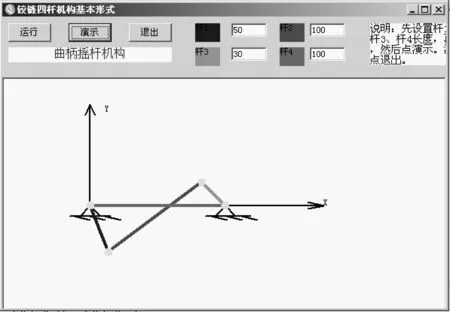
图4 曲柄摇杆机构(3杆为曲柄)
3杆为曲柄时,计算从动杆角度的代码与常规的不同,代码如下。
If ltype = 4 Then '曲柄摇杆,3杆为曲柄
For j = 359 To 0 Step-1
i = j * pi / 180
A = 2 * 杆长(3) * 杆长(1) * Sin(i)
B = 2 * 杆长(1) * (杆长(3) * Cos(i) + 杆长(4))
C = 杆长(2) ^ 2- 杆长(3) ^ 2- 杆长(1) ^ 2- 杆长(4) ^ 2- 2 * 杆长(3) * 杆长(4) * Cos(i)
If (A ^ 2 + B ^ 2- C ^ 2) > 0 Then
从动杆角度(k) = i
atn3 = Atn((A- (Sqr(A ^ 2 + B ^ 2- C ^ 2))) / (B- C))
原动杆角度(k) = 2 * atn3
k = k + 1
End If
Next j
End If
在以上代码中可以看到,当以3杆为曲柄时,相当于把第2节的求解从动杆位置重新再算一遍,只不过这次是以θ3为已知量,θ1为未知量。所以这段代码中B与C的计算公式与常规的是不一样的。此外j也改为从359逆向循环到0,这样是为了使3杆顺时针转动。
4.3.3 双摇杆机构
双摇杆机构,如图5所示。

图5 双摇杆机构
双摇杆机构的主动件与从动件都不能360度转动,所以主动杆角度数组与从动杆角度数组中没有存放360个值;所以在动态运行时,需要用一个变量来控制其转向的切换,代码如下。
If ltype = 2 Then '双摇杆
If switch = 1 Then 'switch控制转向
动画演示循环变量 = 动画演示循环变量 + 1
If 动画演示循环变量 < k Then 'k表示数组中共有几个数据
Call 绘制动画帧(杆长(), 从动杆角度(), 动画演示循环变量, 动画演示窗口)
Else
switch =-1
End If
End If
If switch =-1 Then
动画演示循环变量 = 动画演示循环变量- 1
If 动画演示循环变量 > 0 Then
Call 绘制动画帧(杆长(), 从动杆角度(), 动画演示循环变量, 动画演示窗口)
Else
switch = 1
End If
End If
End If
5 总结
铰链四杆机构仿真教学课件的开发,是对教学资源建设的有益创新与补充,在实际的教学应用中收到了很好的效果。实际上,很多教师都有这种能力,只要把信息化的工具利用起来,开发一些有利于学生理解的课件,一定能显著提高教学效果。
