应用路面平整度预测的数学模型促进黑龙江省高速公路建设

王佳秋 邓慧 王葳 马松林

摘 要：为了更好地贯彻养护工作， 及时采集数据，可以通过路面平整度的时间序列数学模型提出路面平整度预测，建立科学的综合养护方案，以有效测量出路面的真实平整度，避免路面测量过程中检测数据不充分产生的误差，导致不能准确判断路面平整度数据问题。这样，可以降低公路的养护成本，使道路得到及时养护，提高公路的使用寿命。

关键词：最小二乘法；公路养活；回归理论

中图分类号：F540.33 文献标志码：A 文章编号：1673-291X（2016）11-0167-02

随着国民经济迅猛发展，交通物流产业不断扩大，公路使用率剧增。我国高速公路管理单位制定了高速公路日常养护包干管理办法，从而实现“及时养护、防范为主、按时抢修、提高效率、保持检查、预算合理、定期修复”。为了更好地贯彻养护工作， 及时采集数据，通过路面平整度的时间序列数学模型，提出路面平整度预测，建立科学的综合养护方案。研究这种数据的统计方法就是时间序列分析。时间序列数学模型在理论上已趋成熟，它用有限参数线性模型描述时间序列的发展趋势，便于进行统计分析与数学处理，预测高速公路使用年限、路面平整度的变化程度，提出综合养护方案。由于近几年不断发展，具有了科学化的管理措施与养护技术，如果能准确及时提出养护方案，就可以促进提高管理养护水平，同时模型拟合的精度也基本能达到实际工程的要求[1]。

（一）道路数据采集

在实际路面测量中，由于只能测到路面不平度的有限数据，所以我们利用时间序列分析，主要任务就是根据观测到的有限数据，通过时间序列数学模型，利用最小二乘法进行数据拟合，建立尽可能多的数据统计，然后利用模型去解释数据的统计规律，以达到对路面平整度的控制或预报的目的。在时间序列分析中，有两类简单而又常用的模型： 自回归模型（AR）和自回归滑动平均模型（ARMA） [2]。

路面平整度的时间序列模型数据采集是通过自动检测系统完成，其特征在于，要想完成自动化检测系统，需要通过USB接口传输线连接AD转换器，AD转换器连接PLC，PLC连接存储器和数据处理器，数据处理器连接显示屏。可以将自动化检测系统安装在检测车上，检测车上设有测距传感器和定位传感器各8个。我们需要定时采集数据。本文所采集数据是由道路综合检测车对实际路段测得。该设备是由哈尔滨工业大学交通学院侯相深、马松林、王华等人自行开发设计的（见图1所示）。基本原理是通过USB接口，通过传输线将采集的数据直接存入；在检测车上有一个便携式处理器，通过处理器进行数据处理。哈工大设计的工程检测车，由于是由16个传感器所组成，因而每次可以测量一个行车路面的16个点，每次每组得到16个检测数据[3]。

（二）对测量数据序列进行预处理

（三）模型识别和定阶

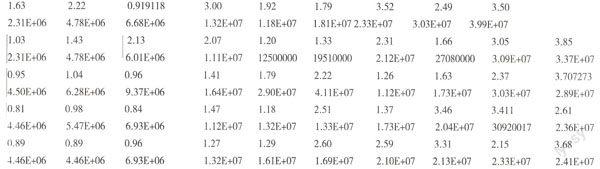
当我们对AR模型确定了16阶次，通过数学模型中的参数的确定，判断路面的平整度指标，由所给样本进行参数估计。而模型参数估计的方法有矩方法、最小二乘法和极大似然法。所给数据得到的样本如果满足正态分布，可以采用最小二乘法进行参数估计。最小二乘法的原理，就是残差平方和达到最小条件下，所得到的对未知参数的估计值。也可以采用极大似然法进行参数估计，得到和最小二乘法基本一致的结果。由于时间序列数学模型仅依赖于有限参数——自回归系数、滑动平均系数及输入白噪声的方差。根据实际路面数据，如下表。

第一行：路面平整度指标 ；

第二行：标准轴载作用次数N。

所以根据数据的统计样本，代人数学模型，发现统计规律，由所得的路面平整度的数量指标，得到判断结果和误差范围。但道路过程不具有遍历性，该实测数据为非标准道路，所以可以根据非标准道路时序模型进行参数估计和预估统计结果[5]。

由统计数据代入时间序列数学模型，可以通过统计软件进行拟合，拟合后的曲线可以看出有明显的趋势性，路面具有时间序列平稳化特点。路面变化也服从平稳化发展趋势。在前面已经给出了平稳化的方法，该方法中较有效的方法是采用差分法，若一次差分后所得的结果不随时间变化具有平稳化，如果序列还不满足平稳性条件，则可以进行二次差分，直到得到的时间序列是平稳变化为止[6]。

以上我们根据哈绥高速路面和天津高速的实测数据，代入路面平整度数学模型判定路面等级，经过检验，确定误差估计范围，可以准确确定路面的整体状况。按照数据统计规律，通过时序模型预测路面平整度，有利于提前做好路面养护方案，落实责任。通过以上方法可以保证黑龙江省公路建设的有效实施。通过黑龙江省公路建设的不断完善和发展，促进该省经济建设，提高经济发展速度。

参考文献：

[1] 袁治.关于高速公路维修保养的几点意见[J].科技资讯，2010，（11）：107.

[2] 刘次华.随机过程[M].武汉：华中理工大学出版社，2000：187-189

[3] 王佳秋，王崴，邓慧，马松林.路面平整度的时间序列模型[J].大学数学2013，（10）：96-102.

[4] 王行建，刘欣.ARMA时间序列模型的研究与应用[J].自动化技术与应用，2008，27 （10）：1-3.

[5] 黄建洪，陈志伟，傅戈雁.时间序列预测模型的建模方法与应用[J].机械制造，2007，11（5）：1-2.

[6] 侯相深.车辙仪的开发要点[J].哈尔滨工业大学学报，2004，（3）：1-3.