多维地震作用下桥梁－无砟轨道非线性相互作用

闫 斌， 刘 施， 戴公连， 蒲 浩， 唐进锋

（1.中南大学 土木工程学院，湖南 长沙 410075；2.高速铁路建造技术国家工程实验室，湖南 长沙 410075）

目前，我国高速铁路线上桥梁比例达50%以上，其中90%的桥梁形式为32m双线无砟轨道简支梁桥［1］。桥上普遍采用无砟轨道无缝线路，如CRTSⅠ型双块式、CRTSⅡ型板式及CRTSⅢ型双块式等。其中，桥上CRTSⅡ型纵连板式无砟轨道结构形式最为特殊，其采用纵向连续的底座板结构代替钢轨成为纵向力的主要承力部件［2］，底座板与桥面板之间通过设置滑动层减小桥梁与轨道结构间的相互作用［3］。

国内外学者对静动力荷载作用下桥上无砟轨道结构系统传力机理及力学特性已进行了较为广泛的研究［4－7］，但鉴于 CRTSⅡ型板式无砟轨道系统结构的复杂性，对地震作用下桥上CRTSⅡ型板式无砟轨道系统受力特性的研究相对较少，其地震响应特征、轨道系统变形规律仍不明确［8－11］。此外，水平地震激励角对系统受力变形的影响，三向地震耦合作用下系统动力响应规律等相关研究很少。

为探讨多维地震作用下桥梁－无砟轨道非线性相互作用规律，本文以沪昆高速铁路上某16×32m简支箱梁桥为例，建立了充分考虑轨道结构层间纵横竖向非线性约束的桥上CRTSⅡ型板式无砟轨道系统仿真模型，与非“纵连”的CRTSⅠ型双块式轨道结构相比较，探讨该系统地震响应特征，首次分析了水平地震激励角对系统受力、变形的影响，探讨了纵向、横向、竖向及三向耦合地震作用下系统地震响应规律，为震区桥上无砟轨道系统的设计和养护维修提供参考。

1 桥梁－无砟轨道非线性相互作用模型

以桥上CRTSⅡ型纵连板式无砟轨道系统为例，计算模型中，钢轨为CHN60轨，扣件采用 WJ－8型，其纵向力－位移关系可表示为［12］

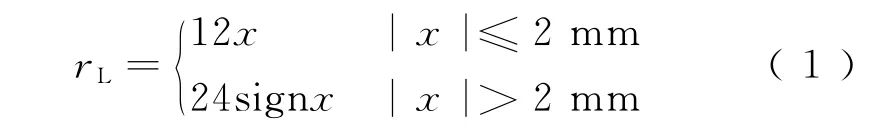
式中：rL为扣件纵向阻力，kN；x为钢轨与承轨台之间的相对位移，mm。

扣件横向阻力采用试验拟合结果表示为

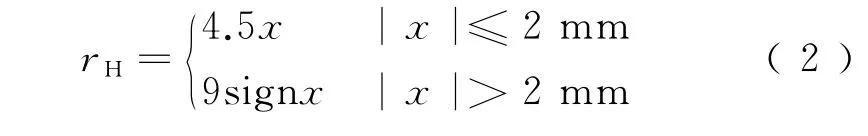
式中：rH为线路纵向阻力，kN；x为钢轨与承轨台之间的相对位移，mm。

扣件竖向刚度取决于扣件的受力状态、垫板及弹条的竖向刚度，其竖向阻力－变形曲线见图1。

图1 扣件竖向阻力-变形曲线

预制轨道板尺寸为6.45m×2.55m×0.20m，采用C55混凝土。用张拉锁件连接纵向钢筋使轨道板纵向连续。轨道板和底座板之间填充水泥乳化沥青砂浆，砂浆层纵横竖向刚度采用文献［13］所取得的试验参数。底座板尺寸为2.95m×0.19m×0.20m，采用C30混凝土，纵向连续铺设。

底座板与梁体间设置滑动层，滑动层采用仅受压的理想弹塑性弹簧模拟，弹塑性分界点变形取为0.5 mm，纵横向滑动摩阻系数取为0.3［14］。

为防止底座板产生大幅度纵向滑移，在固定支座处，通过剪力齿槽将底座板锚固在梁体上。路基段摩擦板长50m，摩擦系数取为0.7。采用倒T形端刺，假设路基为刚性支撑，端刺外侧取250m长的路基段。

桥梁范围内每隔15m设置1个扣压式挡块，挡块仅约束轨道结构竖向和横向变形。考虑到后浇挡块与底座板间存在极为微小的缝隙（此处取为1mm），将挡块与底座板间的相互作用按仅受拉hook单元模拟，其刚度取极大值1×108kN／m。

桥梁为双线无砟轨道32m预应力混凝土简支箱梁。滑动支座采用理想弹塑性模型，摩擦系数取为0.3，弹塑性分界点变形为3mm。

2＃～16＃桥墩高度均为20m，为圆端形截面，墩体采用C40混凝土，墩壁内外侧各布置双层直径16 mm的纵筋，桥墩采用非线性纤维梁单元模拟，混凝土采用考虑箍筋约束的Mander－Confined模型，其截面弯矩－曲率曲线见图2。

图2 桥墩弯矩-曲率曲线

桩－土共同作用采用6自由度的等效刚度矩阵模拟，建立的有限元模型见图3（a）。此外，建立了16×32m简支箱梁桥－CRTSⅠ型双块式无砟轨道系统仿真模型，见图3（b）。钢轨、扣件、桥梁、下部结构等设计参数与图3（a）保持一致。

图3 本文建立的有限元模型

图3中水平地震激励角θ为地震激励方向与桥梁走向间的夹角，0°为纵向激励，90°为横向激励。

系统采用Rayleigh阻尼，阻尼比h取为0.05，阻尼系数α和β为

式中：ω1和ω2分别为第1阶和对结构纵向振型贡献最大的一阶频率。

地震设防烈度为8度，采用El－centro波，保留地震波的频谱特性，仅将最大峰值加速度调至0.57g（罕遇地震）［15］，地震波持续时间为包含地震动峰值的前30s。

2 桥上CRTSⅡ型轨道系统地震响应特征

2.1 纵向地震作用

分析纵向地震（0.57g El－centro波）作用下，桥上CRTSⅠ型轨道系统（以下简称“模型Ⅰ”）和桥上CRTSⅡ型轨道系统（以下简称“模型Ⅱ”）的动力响应，得到系统的受力、变形规律，见图4。

图4 纵向地震作用下系统受力、变形规律

由图4可以看出，2个模型的钢轨应力包络曲线均关于跨中成反对称分布，最大值均出现在桥台附近；模型Ⅱ钢轨应力包络曲线较为平滑，与模型Ⅰ相比，模型Ⅱ钢轨应力减少33.3%，最大拉应力值为141.1 MPa。

纵向地震作用下，2个模型桥台底部均承受较大纵向剪力，分别为21 570.7kN（模型Ⅱ），21 081.9kN（模型Ⅰ）；桥墩受力均较为均衡，数值相差不大。

对于模型Ⅱ，由于滑动层摩擦系数极小，地震作用下滑动层出现较大纵向位移，其峰值出现在各简支梁的活动支座附近，最大值为24.4mm。桥面板与底座板之间通过滑动层滞回耗能有利于提高桥上CRTSⅡ型轨道系统的抗震性能。

2.2 竖向地震作用

将竖向地震作用取为水平地震加速度的65%，分析竖向地震作用下2个模型的动力响应，得到系统受力、变形规律见图5。

图5 竖向地震作用下系统受力、变形规律

由图5可知，由于模型Ⅱ滑动层仅受压不受拉，故竖向地震作用下，其钢轨拉应力普遍较大，为25.9 MPa（桥台附近），模型Ⅰ钢轨应力最大值为15.8MPa（压应力）。

模型Ⅱ扣件竖向变形也较大，其最大值出现在桥台附近，为0.3mm。挡块对轨道竖向变形有一定约束作用，地震中挡块与底座板之间存在频繁碰撞现象。

3 水平地震激励角的影响

分析水平地震激励角θ分别为0°、45°、90°时2个模型的动力响应，得到的钢轨应力包络曲线见图6，墩底最大剪力见图7，扣件纵向变形见图8，钢轨节点横向位移见图9。

由图6可知：各角度水平地震作用下，2个模型钢轨应力包络曲线均关于跨中大致成反对称分布；随着地震激励角的不断增大，钢轨应力不断减小；模型Ⅱ钢轨应力包络曲线较为平滑，钢轨应力最大值分别为141.1MPa（θ＝0°）、7.3MPa（θ＝90°）。

由图7（a）可知：水平地震激励角越大，墩底最大纵向剪力越小；桥台承受最大纵向剪力θ＝90°时不足10kN，θ＝0°时达21 570.7kN；地震激励角度对其他桥墩影响较小。

图6 水平地震作用下钢轨应力包络曲线

图7 水平地震作用下墩底最大剪力

由图7（b）可知：2个模型墩底最大横向剪力均关于跨中成轴对称分布，最大值均出现在5＃墩和13＃墩墩底；随着水平地震激励角的不断增大，墩底横向剪力不断增大；θ＝0°时，2模型墩底最大横向剪力不超过10kN；θ＝90°时，5＃墩墩底最大横向剪力分别为14 363.4kN（模型Ⅱ）、13 253.7kN（模型Ⅰ）。

由图8可知：2个模型扣件纵向变形随着水平地震激励角的增大而逐渐减小；模型Ⅰ扣件纵向变形最大值出现在桥台附近，最大值分别为48.3mm（θ＝0°）、0.3mm（θ＝90°）；模型Ⅱ扣件纵向变形最大值出现在端刺附近，最大值分别为2.1mm（θ＝0°）、0.2 mm（θ＝90°）。

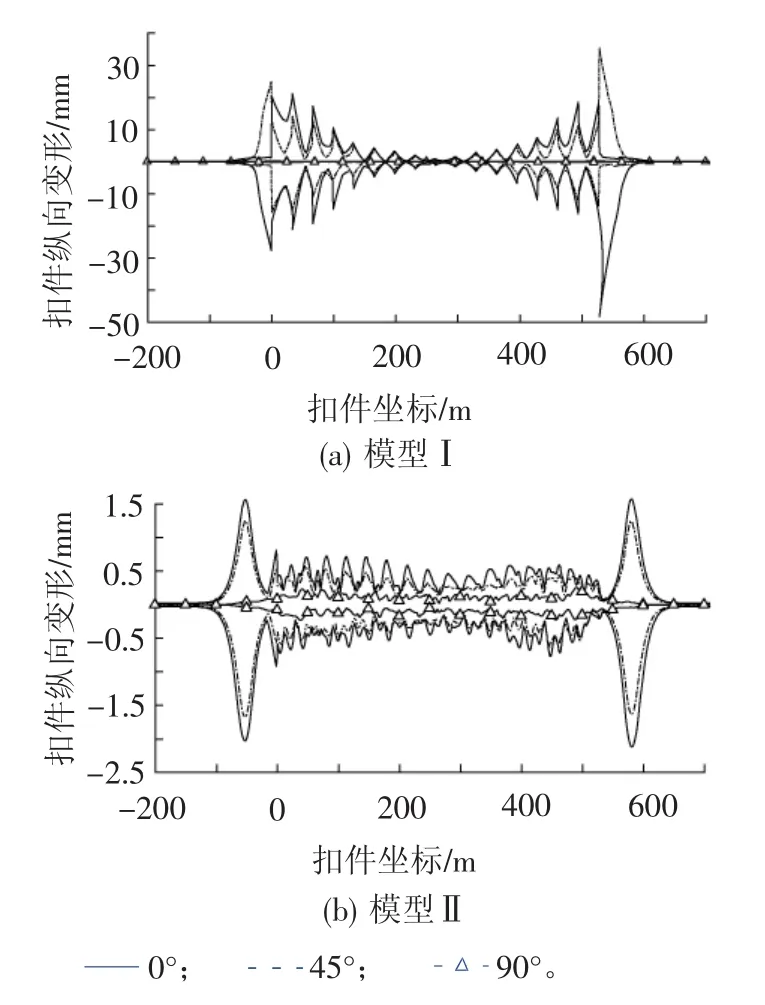
图8 水平地震作用下扣件纵向变形

图9 水平地震作用下钢轨节点横向位移

由图9可知：2个模型钢轨节点横向位移包络曲线关于跨中大致成轴对称分布；水平地震激励角越大，钢轨节点横向位移越大；θ＝0°时，2个模型钢轨节点横向位移较小，最大值为0.1mm；θ＝90°时，钢轨节点横向位移最大值分别为39.6mm（模型Ⅰ）、46.8mm（模型Ⅱ）。

水平地震激励角对系统受力、变形影响较大，在进行地震响应计算时应予以考虑。

4 多维地震耦合作用下系统受力及变形规律

分析纵向、横向、竖向及三向地震耦合作用下2个模型的动力响应，得到的钢轨应力包络曲线见图10，扣件纵向变形规律见图11，钢轨节点横向绝对位移见图12，钢轨节点竖向绝对位移见图13。

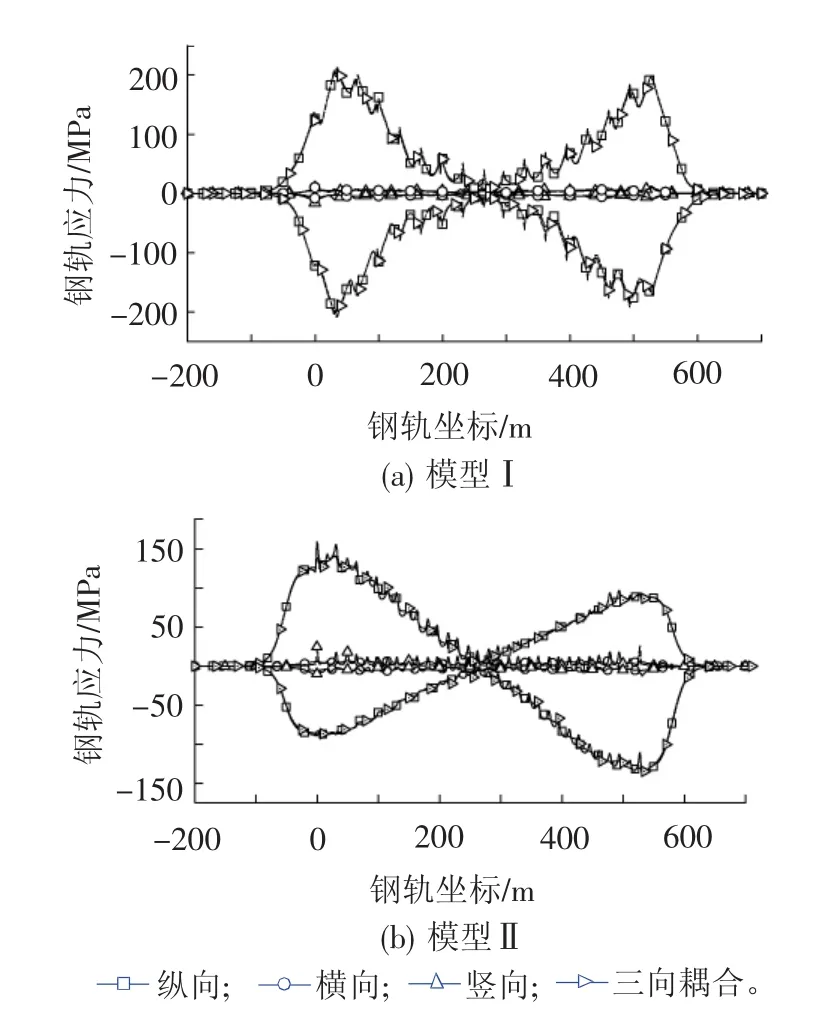
图10 不同方向地震作用下钢轨应力包络曲线

图11 不同方向地震作用下扣件纵向变形规律

由图10、图11可知，三向地震耦合作用与纵向地震作用相比，钢轨应力包络曲线大致重合，扣件纵向变形最大值基本相等，证明纵向地震起控制作用。

图12 不同方向地震作用下钢轨节点横向绝对位移

图13 不同方向地震作用下钢轨节点竖向绝对位移

由图12可知：三向地震耦合作用下钢轨节点横向位移包络曲线与横向地震作用下包络曲线基本重合；模型Ⅱ钢轨节点横向位移最大值为46.8mm，与模型Ⅰ相比增大18.2%；纵向和竖向地震作用对钢轨节点横向位移影响较小。

由图13可知：对于模型Ⅰ而言，纵向、竖向及三向地震耦合作用时，钢轨节点竖向位移波动均较大，其峰值出现在各简支梁跨中处，最大值均出现在桥台附近；桥台处钢轨节点竖向位移在耦合地震作用下最大，为16.2mm，纵向地震作用下次之，为12.8mm，竖向地震作用下最小，为5.3mm；横向地震作用下，钢轨节点竖向位移包络曲线较为平滑，竖向位移最大值为5.7mm。

竖向和三向地震耦合作用下，模型Ⅱ钢轨节点竖向位移均较大，最大值分别为192.4mm（竖向）、202.9mm（耦合）、38.5mm（纵向）、37.1mm（横向）。证明模型Ⅱ竖向约束相对较弱，震后有可能存在较大的竖向残余变形。

5 结论

为研究多维地震作用下桥上无砟轨道系统地震响应规律，建立了充分考虑钢轨、扣件、轨道板、砂浆层、底座板、滑动层、桥梁、固结机构、端刺、挡块等部件的16×32m简支梁桥－CRTSⅡ型无砟轨道仿真模型，并与桥上CRTSⅠ型双块式无砟轨道对比，探讨地震作用下桥上无砟轨道系统地震响应特征，及水平地震激励角及多向地震耦合作用对地震响应的影响规律。主要结论如下：

（1）与模型Ⅰ系统相比，地震作用下模型Ⅱ钢轨应力包络曲线较为平滑，且数值大幅减小，滑动层纵竖向位移均较大，具有滞回耗能的作用。竖向地震作用下，桥上CRTSⅡ型轨道系统钢轨所受拉应力较大，挡块对轨道竖向变形起到了一定的约束作用；震时底座板与挡块之间存在着频繁碰撞现象；轨道结构竖向约束相对较弱，震时其钢轨竖向位移较大。

（2）水平地震激励角与系统地震响应峰值密切相关。水平地震激励角越大，桥上无砟轨道系统的钢轨应力、墩底最大纵向剪力和扣件纵向变形越小，墩底最大横向剪力和钢轨节点横向位移越大，在进行地震响应分析时应予以考虑。

（3）纵向地震作用对钢轨应力、扣件纵向变形起控制作用，横向地震作用对钢轨横向绝对位移起控制作用，竖向地震作用对钢轨竖向绝对位移起控制作用。考虑三向地震耦合作用时，2个模型钢轨节点竖向位移比竖向地震单独作用大5.5%～205.7%。在进行地震响应分析时，应重点考虑钢轨节点竖向位移的耦合效应。

参考文献：

［1］YAN Bin，DAI Gonglian，HU Nan.Recent Development of Design and Construction of Short Span High－speed Railway Bridges in China［J］.Engineering Structures，2015，100：707－717.

［2］Bgl Company of German.Number 4Technical Report of Bogl Longitudinal Connected Ballastless Track on Jing－Jin Intercity High－speed Railway Bridges［R］.Tianjin：Jing－Jin Intercity High－speed Railway Design Department of Bgl Company of German，2006.

［3］Bgl Company of German.Number 7Technical Report of Bogl Longitudinal Connected Ballastless Track on Jing－Jin Intercity High－speed Railway Bridges［R］.Tianjin：Jing－Jin Intercity High－speed Railway Design Department of Bgl Company of German，2006.

［4］UIC.UIC 774－3Track／bridge Interaction：Recommendations for Calculations［S］.Paris：International Union of Railways，2001.

［5］徐庆元，范浩，李斌.无砟轨道温度梯度荷载对列车－路基上板式无砟轨道系统动力特性的影响［J］.铁道科学与工程学报，2013，10（3）：1－6.XU Qingyuan，FAN Hao，LI Bin.Influence of Temperature Gradient Load of Slab on Dynamic Characteristic of Train－slab Track on Subgrade System［J］.Journal of Railway Science and Engeneering，2013，10（3）：1－6.

［6］闫斌，戴公连，徐庆元.行波效应下铁路简支梁桥梁轨系统地震响应［J］.振动工程学报，2013，36（3）：357－362.YAN Bin，DAI Gonglian，XU Qingyuan.Longitudinal Interaction of Simply－supported Beams and CWR under Traveling Wave［J］.Journal of Vibration Engineering，2013，36（3）：357－362.

［7］YAN Bin，DAI Gonglian.Seismic Pounding and Protection Measures of Simply－supported Beams Considering Interaction Between Continuously Welded Rail and Bridge［J］.Structural Engineering International，2013，23（1）：61－67.

［8］ZHANG Nan，ZHOU Shuang，XIA He，et al.Evaluation of Vehicle－track－bridge Interacted System for the Continuous CRTS－Ⅱ Non－ballast Track Slab［J］.Science China Technological Sciences，2014，57（10）：1 895－1 901.

［9］林红松，刘学毅，杨荣山.大跨桥上纵连板式轨道受压稳定性［J］.西南交通大学学报，2008，43（5）：673－678.LIN Hongsong，LIU Xueyi，YANG Rongshan.Compressive Stability of Continuous－slab－track on Long－span Bridge［J］.Journal of Southwest Jiaotong University，2008，43（5）：673－678.

［10］SUN Lu，CHEN Liliang，ZELELEW H H.Stress and Deflection Parametric Study of High－speed Railway CRTSⅡBallastless Track Slab on Elevated Bridge Foundations［J］.Journal of Transportation Engineering，2013，139（12）：1 224－1 234.

［11］朱乾坤，戴公连，闫斌.简支梁－CRTSⅡ型板式无砟轨道制动力传递规律［J］.铁道科学与工程学报，2014，11（6）：13－19.ZHU Qiankun，DAI Gonglian，YAN Bin.Transfer Law of Breaking Force Between Simply－supported Bridges and CRTSⅡ Slab Ballastless Track［J］.Journal of Railway Science and Engineering，2014，11（6）：13－19.

［12］中华人民共和国铁道部.TB 10015—2012铁路无缝线路设计规范［S］.北京：中国铁道出版社，2012.

［13］粟淼.高速铁路桥上纵连板式无砟轨道层间界面工作性能初探［D］.长沙：中南大学，2014.

［14］邱远喜.长联大跨连续梁桥上CRTSⅡ型板式无砟轨道受力特性研究［D］.长沙：中南大学，2014.

［15］中华人民共和国铁道部.GB 50111—2006铁路工程抗震设计规范［S］.北京：中国计划出版社，2006.