基于连续损伤模型空气弹簧疲劳寿命分析

丁智平， 李志超， 何 园， 李雪冰， 黄达勇

（1.湖南工业大学 机械工程学院，湖南 株洲，412007；2.清华大学 汽车安全与节能国家重点实验室，北京100084；3.中车青岛四方车辆研究所有限公司，山东 青岛 266031）

随着我国高速列车的快速发展，在保证安全性前提下，人们对运行过程中轨道车辆的运行质量提出了更多的要求。轨道车辆高速运行时，由于受到外界环境干扰，产生不同程度的横向和垂向振动，这对轨道车辆的正常运行具有较大的影响。如何缓解轨道车辆运行过程中产生的振动激励，成为当前提高轨道车辆运行质量的首要问题。作为轨道车辆运行过程中的减振元件，空气弹簧因其优越的减振性能而被广泛应用于轨道交通高速车辆的悬挂系统。空气弹簧工作变形大，在多向载荷工况下处于复杂应力状态，其主要失效形式之一是橡胶材料的疲劳破坏。

当前，研究橡胶疲劳的方法有二种：一是以连续介质力学为基础的裂纹萌生法，该方法是通过给定的损伤参量预测橡胶的疲劳裂纹萌生寿命［1］；二是以断裂力学为基础的疲劳裂纹扩展法，该方法是在已知裂纹几何信息、裂纹扩展速率与撕裂能之间的幂率关系等条件下，预测橡胶的疲劳裂纹扩展寿命。Luo［2－3］等人提出根据3个主应力计算相应等效应力的计算公式，并以计算得到的等效应力范围作为橡胶寿命预测的损伤参量，对轨道车辆上使用的橡胶减震器进行寿命评估；丁智平［1，4］等人利用连续损伤力学概念，基于一阶Ogden应变能函数，导出用于橡胶材料寿命预测的连续损伤预测模型，并对轨道车辆上使用的橡胶球铰进行了寿命评估。王文涛［5］等人基于线性累计损伤概念，对汽车发动机悬置进行了相应的寿命评估。Tomita［6］等人根据损伤理论提出橡胶材料损伤演化模型和寿命评估方法。Gdoutos［7］等人分析了断裂力学在橡胶材料中的应用，并根据实验结果确定了能量释放率与裂纹扩展之间的函数关系。Lake［8－9］等人提出了橡胶材料裂纹扩展速率与撕裂能之间满足幂函数关系，撕裂能确定的状况下，可以通过相应的函数关系计算出橡胶材料的疲劳裂纹扩展寿命。丁智平［10］等人通过橡胶纯剪切裂纹扩展实验，确定了裂纹扩展速率与撕裂能之间的幂函数关系，并提出以撕裂能范围作为橡胶材料裂纹扩展寿命预测的损伤参量，对轨道交通中使用的橡胶弹性元件进行寿命评估。张国富［11］基于虚拟疲劳实验提出了空气弹簧寿命预测方法，对轨道车辆上使用的空气弹簧进行寿命预测，并对空气弹簧的损伤原因进行分析。Mars［12］提出橡胶多轴加载时，只有部分应变能密度用于裂纹扩展，将这部分应变能定义为开裂能密度，其作为损伤参量被用于空气弹簧的寿命预测［13］。

基于断裂力学和连续介质力学理论的疲劳寿命评估方法，虽然在橡胶疲劳领域中应用广泛，国内外相关的文献也非常多，但是关于空气弹簧疲劳寿命研究的相关文献却较少。轨道车辆中使用的空气弹簧的结构和承载工况复杂，很难准测地评估其疲劳寿命，考虑到轨道车辆的运行安全，大部分空气弹簧都是在未到达使用年限前更换，这样就造成巨大的社会资源浪费。本文基于连续介质损伤力学理论，研究了空气弹簧寿命预测方法，为空气弹簧的研发、设计提供了理论指导。

1橡胶材料疲劳损伤寿命模型

1.1 Ogden超弹性本构模型

橡胶是典型的超弹性材料，用应变能函数表征其力学特征，对其求导即可得到应力－应变关系，Ogden模型函数表达式为

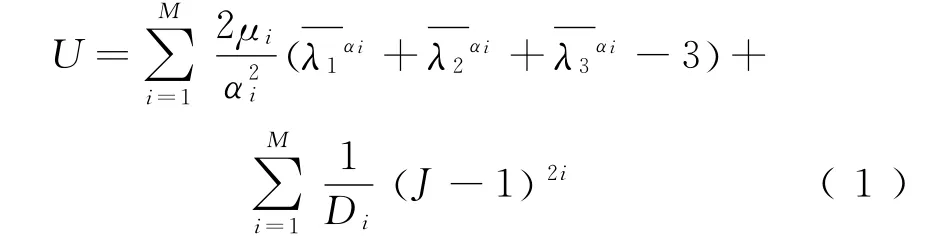
式中由于橡胶材料的不可压缩性，J＝λ1λ2λ3＝1，即为主伸长比；αi、μi为材料常数，通过拟合材料力学性能实验数据确定；M 为Ogden模型的阶数；Di为材料常数，根据橡胶材料初始体积模量确定。

在单向拉伸状态下，应力与应变之间的关系为

式中：σU为单向拉伸状态下的应力。

由于一阶Ogden本构模型［1］不适用于橡胶大变形的情况，而空气弹簧的工况是大变形。因此，采用三阶Ogden本构模型推导损伤演化方程，在单向应力状态下其应变能函数可表示为

因而，在单向应力状态下应力与应变的关系为

式中：材料常数αi、μi可通过材料本构试验数据拟合得出。

1.2 连续损伤寿命预测模型

橡胶弹性元件内部由于周期循环载荷导致疲劳累计损伤，最终失效。Lemaitre［14］基于连续介质损伤力学，通过定义一个损伤因子D获得损伤应力，损伤应力表达式为

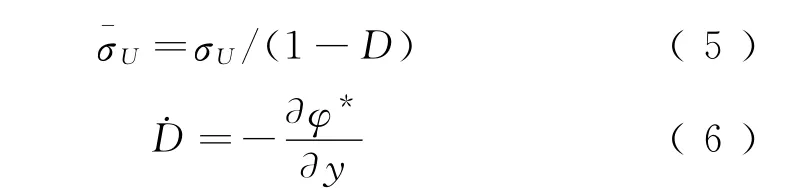
式中为损伤应力；D为损伤率；φ＊为耗散势能函数；y为损伤应变能释放速率。

将式（4）代入式（5）得损伤应力为

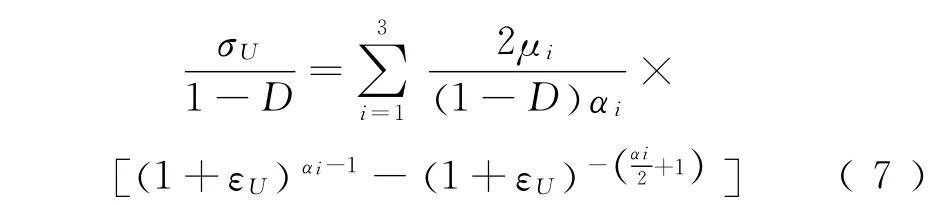
耗散势能函数形式为

式中：a、b为材料常数，通过拟合橡胶材料疲劳实验数据确定。

Tang［15］等人根据材料未损伤应变能函数表达式与损伤应变能函数表达式的一致性，定义了损伤应变能是关于损伤应力的函数。因此，损伤应变能释放率表达式为

因此，损伤应变能释放速率为

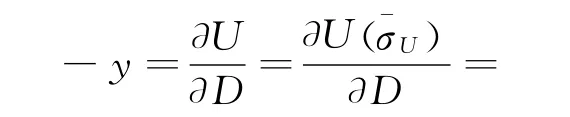
根据正交法则，可导出损伤演化方程为

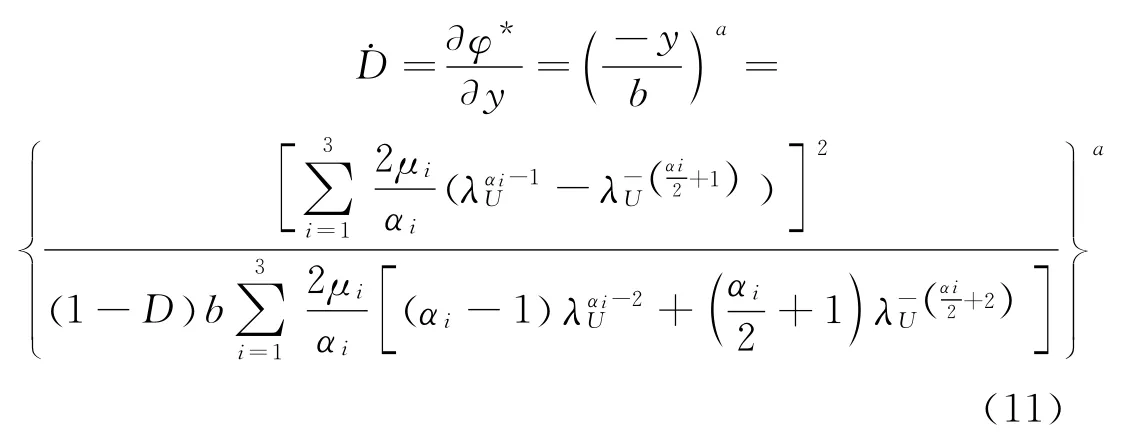
因此，单个循环下的疲劳损伤为

式中：ΔλU为主伸长范围；N 为循环周期。

对上式进行积分，根据初始未损伤条件：N＝0，D＝0和最终疲劳破坏条件：N＝Nf、D＝1，得到橡胶材料连续损伤寿命预测模型表达式为

因为ΔλU＝1＋ΔεU，疲劳寿命可以根据产品在疲劳载荷下相应的应变范围得出

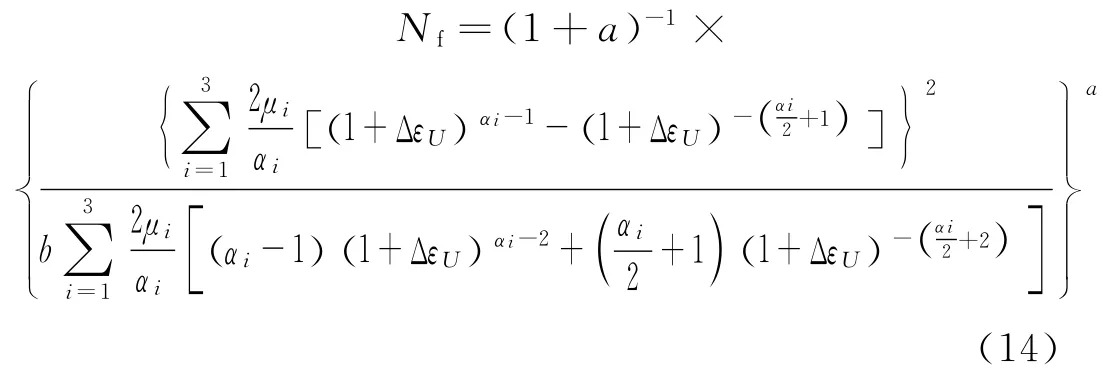
1.3 等效应变计算

基于连续损伤力学的寿命预测模型是在单向应力状态下推导得出，而橡胶弹性元件实际承载工况多为复杂应力状态，为了将其应用于实际，利用等效应变范围代替寿命预测模型中的应变范围。Luo［2－3］提出根据3个主应力获得等效应力σf的计算公式，计算等效应力σf的表达式为

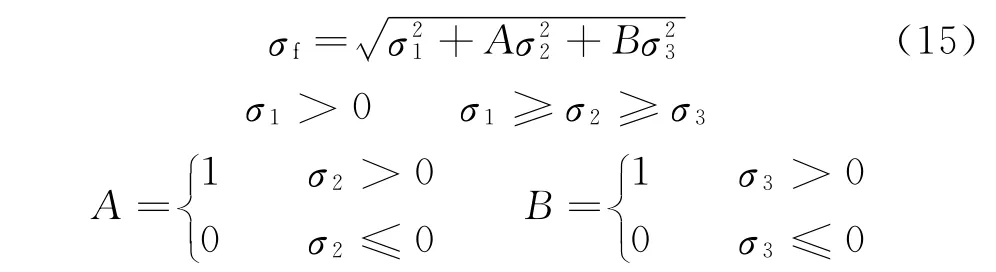
式中：σf为等效应力；σ1、σ2、σ3为主应力，等效应变由单轴拉伸实验获得的应力－应变关系确定。

1.4 单轴拉伸实验

无切口单轴拉伸实验试样见图1，试样是在200T电磁平板硫化机上制备的，硫化过程中需要的压力为21MPa、温度为150℃、硫化持续时间为10min，实验前将试样置于温度为（23±1）℃和湿度为50%的环境中6h，然后进行单轴拉伸实验获得应力－应变数据，用于确定橡胶材料的应力－应变关系表达式。

图1 无切口拉伸试样（mm）

单轴拉伸实验是在CMT 4204万能电子试验机上进行的，试样标距为25mm，实验的拉伸速率保持在6mm／min，无切口试样单轴拉伸获得的应力－应变数据见图2。根据实验获得的数据拟合确定橡胶材料应力－应

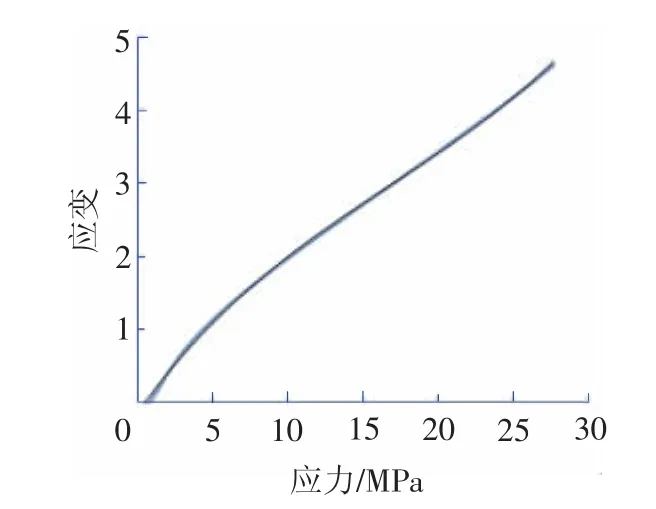
图2 无切口拉伸试样的应力-应变关系曲线

变关系表达式为

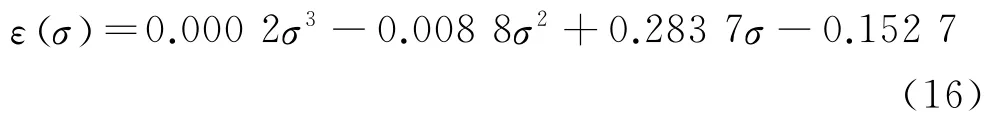
1.5 确定模型参数a、b

考虑到空气弹簧使用工况复杂，承受负载较大，属于大变形。参照 MARS［16－17］关于橡胶材料多轴疲劳试验研究，选择其中大部分多轴疲劳试验数据用于拟合疲劳寿命预测模型，见式（14），确定模型参数a、b，多轴疲劳试验加载路径见图3，多轴疲劳试验数据见表1。

图3 拉-扭加载路径图

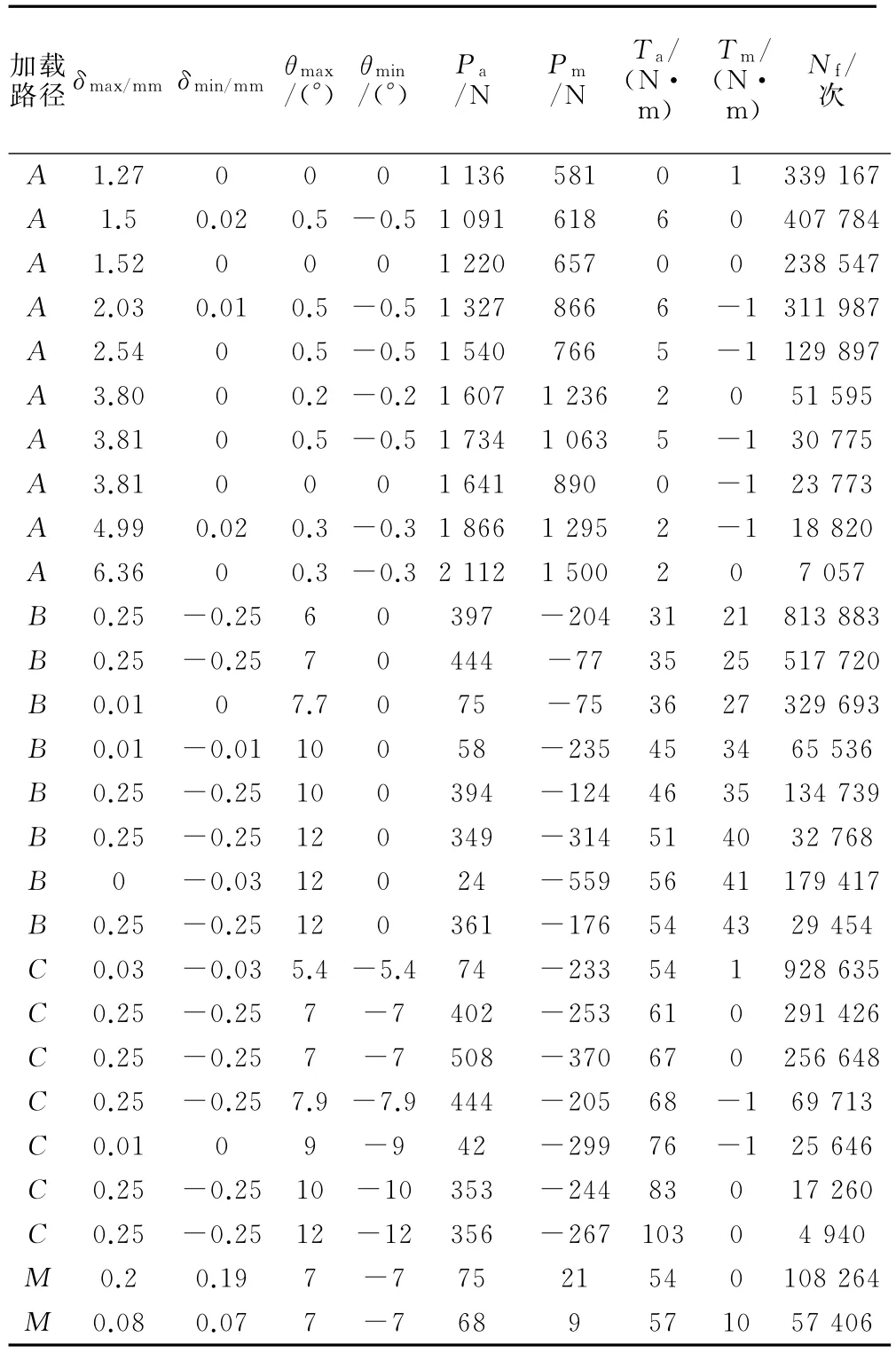
表1 多轴疲劳试验数据

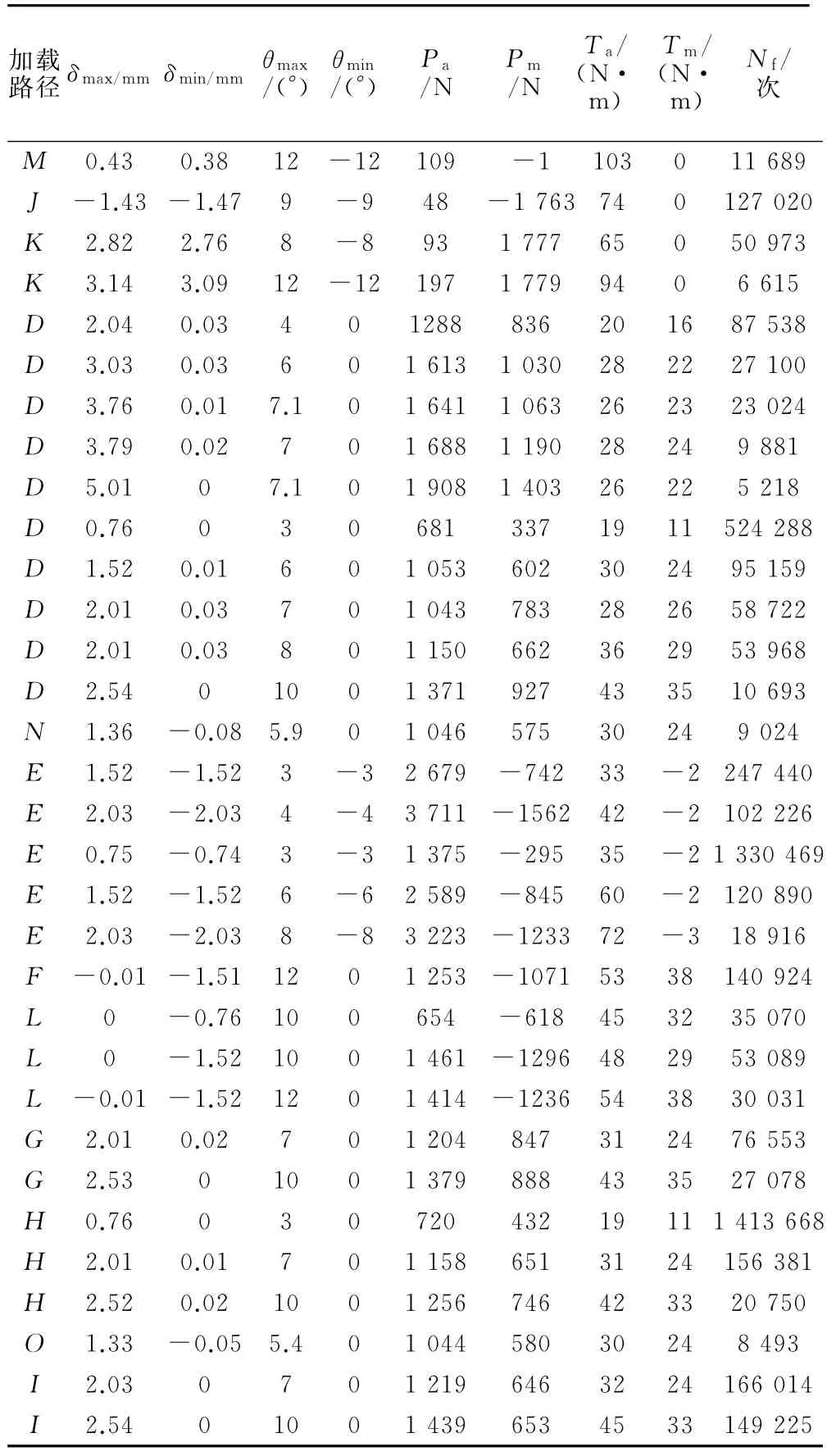
续表1 多轴疲劳试验数据

选择多轴疲劳试验数据，利用有限元软件对疲劳试样进行仿真，结果见图4。提取危险位置的3个主应力，再利用式（15）计算得出等效应力，然后利用式（16）求出对应的等效应变和等效应变范围，最后拟合多轴疲劳试验数据得出a、b。

图4 疲劳试样最大主应变分布云图

对式（14）二边取对数得

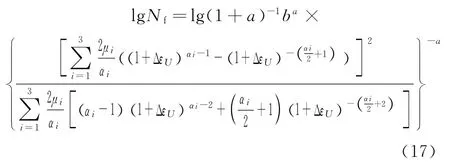
将其转化成Y＝AX＋B形式，通过实验数据拟合得出系数A和B，进而求出a和b，得

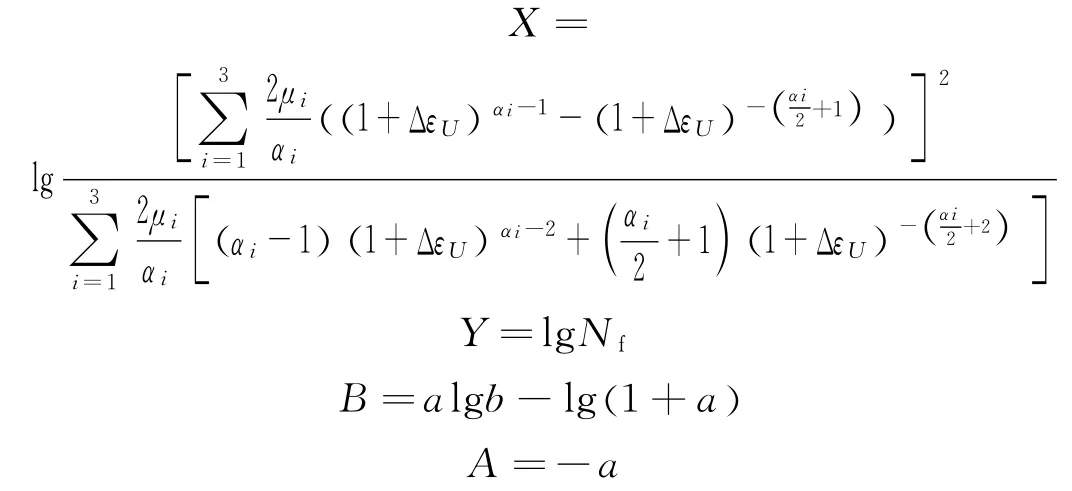
拟合结果见图5。

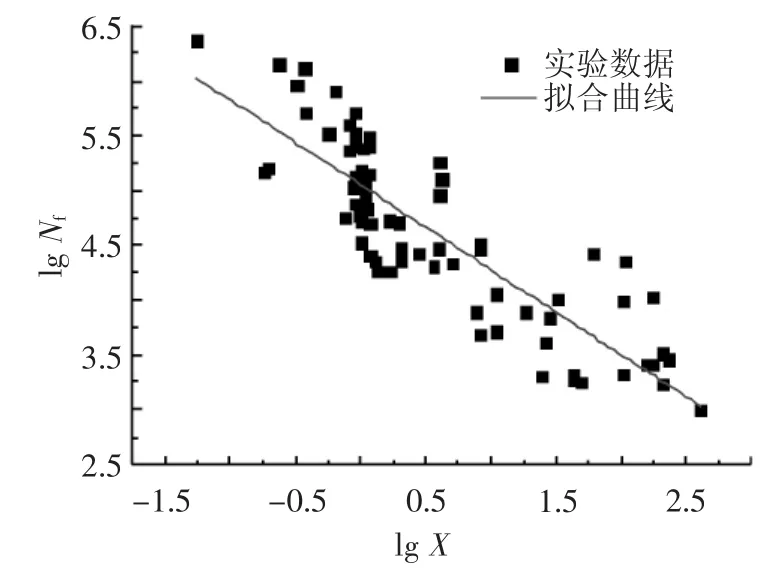
图5 多轴疲劳试验数据拟合效果图

利用多轴疲劳试验数据拟合式（17），得出寿命预测模型参数a＝0.774，b＝7.03×106。

2 空气弹簧有限元分析

2.1 Ogden模型参数的获取

为了对橡胶进行准确的力学性能表征，进行了单轴拉伸、平面拉伸和等双轴拉伸试验，试验在美国Axel实验室进行。利用三阶Ogden模型对力学性能实验数据进行拟合，拟合结果见图6，模型参数值见表2。

表2 三阶Ogden模型参数值

2.2 空气弹簧有限元仿真

2.2.1 载荷工况

空气弹簧的承载工况为：

（1）对上下盖板施加轴向位移固定约束；

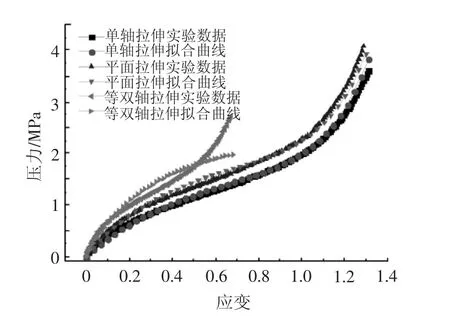
图6 Ogden三阶模型拟合结果

（2）通过定义的流体单元参考点给空气弹簧胶囊内部充入压力为0.65MPa的气体；

（3）对上盖板施加80mm的横向位移载荷。

2.2.2 空气弹簧有限元分析

利用Hypermesh软件对空气弹簧划分网格，然后导入ABAQUS中定义载荷工况和分析步，最后利用其求解器进行模拟仿真，空气弹簧有限元模型见图7。

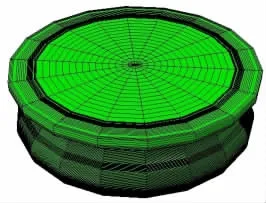
图7 空气弹簧三维有限元模型

利用ABAQUS仿真软件求解器对空气弹簧承载工况进行模拟，得到空气弹簧胶囊部分最大主应力分布等值线云图，提取应力集中部位的横截面，并绘制出充气后空气弹簧应力分布等值线云图和横向加载后应力集中部位的应力分布等值线云图，见图8、图9。

图8 充气后空气弹簧的最大主应力分布等值线图

2.3 空气弹簧疲劳寿命预测

图9 横向位移加载后空气弹簧的最大主应力分布等值线图

由有限元模拟仿真结果知，空气弹簧的疲劳破坏最先发生在应力集中区域。提取应力集中区域上最大主应力单元所对应的3个主应力，由式（15）计算出对应的等效应力，再由式（16）计算出对应的等效应变和等效应变范围。

危险位置在充气后所对应的主应力、等效应力和等效应变见表3。

表3 充气后空气弹簧危险位置的相关参数

危险位置在横向加载后所对应的主应力、等效应力和等效应变见表4。

空气弹簧的加载工况先充气，然后周期横向位移加载，因此，计算得到的等效应变范围见表5。

将求得的危险位置的等效应变范围和相关材料参数代入寿命预测模型（14），即可得到空气弹簧裂纹萌生疲劳寿命为Nf＝30 719次

表4 横向位移加载后空气弹簧危险位置的相关参数

表5 空气弹簧危险位置的等效应变范围

3 空气弹簧疲劳试验

根据轨道车辆运行过程中空气弹簧的实际承载工况，对空气弹簧进行疲劳验证性实验，实验得到疲劳断口位置见图10，空气弹簧疲劳破坏次数为62 200次。

图10 空气弹簧胶囊疲劳断口图

根据空气弹簧疲劳实验得到的疲劳断口位置，可以看出实验得到的疲劳位置与寿命预测的危险位置基本一致，验证了有限元模拟仿真的可行性，为空气弹簧的设计和优化提供了有效的方法。空气弹簧疲劳寿命的预测值较实验值小，实验值与预测值之比为62 200／30 719＝2.02，满足工程疲劳寿命预测精度的要求，对空气弹簧的开发具有指导意义。

4 结论

（1）基于连续介质损伤力学理论，结合三阶Ogden应变能密度函数，以等效应变范围为损伤参量推导出橡胶材料疲劳损伤寿命预测模型，并利用多轴疲劳试验数据确定了寿命预测模型参数a和b；

（2）利用有限元仿真技术、等效应力计算方法和单轴拉伸获得的应力－应变关系，计算出空气弹簧危险位置等效应变范围，提出了复杂应力状态下空气弹簧的疲劳寿命分析方法；

（3）利用提出的寿命预测模型对空气弹簧进行寿命评估，并与疲劳实验进行对比，结果显示疲劳寿命实验值与预测值之比为2.02，满足工程预测精度的要求，表明连续损伤寿命预测模型的有效性；

（4）利用连续损伤寿命预测模型，结合有限元数值模拟，可以有效预测空气弹簧的疲劳破坏寿命与危险位置，为空气弹簧的研发提供依据，缩短产品的研发周期。

参考文献：

［1］丁智平，杨荣华，黄友剑，等.基于连续损伤模型橡胶弹性减振元件疲劳寿命分析［J］.机械工程学报，2014，50（10）：80－86.DING Zhiping，YANG Ronghua，HUANG Youjian，et al.Fatigue Life Analysis of Rubber Vibration Damper Based on Continuum Damage Model［J］.Journal of Mechanical Engineering，2014，50（10）：80－86.

［2］LUO R K，WU W X，COOK P W，et al.An Approach to Evaluate the Service Life of Rubber Springs Used in Rail Vehicle Suspensions［J］.Proceedings of the Institution of Mechanical Engineers，Part F：Journal of Rail and Rapid Transit，2004，218（2）：173－177.

［3］LUO R K，COOK P W，WU W X，et al.Fatigue Design of Rubber Springs Used in Rail Vehicle Suspensions［J］.Proceedings of the Institution of Mechanical Engineers，Part F：Journal of Rail and Rapid Transit，2003，217（3）：237－240.

［4］杨荣华.复杂应力状态下橡胶球铰承载特性与疲劳寿命研究［D］.株洲：湖南工业大学，2013.

［5］王文涛，上官文斌，段小成，等.基于线性疲劳累计损伤橡胶悬置疲劳寿命预测研究［J］.机械工程学报，2012，48（10）：56－65.WANG Wentao，SHANGGUAN Wenbin，DUAN Xiaocheng，et al.Study on Prediction of Fatigue Life of Rubber Mount Based on Linear Cumulative Fatigue Damage Theory［J］.Journal of Mechanical Engineering，2012，48（10）：56－65.

［6］TOMITA Y，LU W.Computational Characterization of Micro－to Macroscopic Mechanical Behavior and Damage of Polymers Containing Second－phase Particles［J］.International Journal of Damage Mechanics，2002，11（2）：129－149.

［7］GDOUTOSE E，DANIEL I M，SCHUBEL P.Fracture Mechanics of Rubber［J］.Automatic Control and Robotics，2003，3（13）：497－510.

［8］GENT A N，LINDLEY P B，THOMAS A G.Cut Growth and Fatigue of Rubbers.I.The Relationship Between Cut Growth and Fatigue［J］.Journal of Applied Polymer Science，1964，8（1）：455－466.

［9］LAKE G J，LINDLEY P B.Cut Growth and Fatigue of Rubbers.II.Experiments on a Noncrystallizing Rubber［J］.Journal of Applied Polymer Science，1964，8（2）：707－721.

［10］丁智平，陈吉平，宋传江，等.橡胶弹性减振元件疲劳裂纹扩展寿命分析［J］.机械工程学报，2010，46（22）：58－64.DING Zhiping，CHEN Jiping，SONG Chuanjiang，et al.Analysis of Fatigue Crack Growth Life for Rubber Vibration Damper［J］.Journal of Mechanical Engineering，2010，46（22）：58－64.

［11］张国富.城市轨道车辆空气弹簧系统使用寿命及可靠性评价方法［D］.上海：上海工程技术大学，2013.

［12］MARS W V.Cracking Energy Density as a Predictor of Fatigue Life under Multiaxial Conditions［J］.Rubber Chemistry and Technology，2002，75（1）：1－17.

［13］李志超，李雪冰，刘万强，等.轨道车辆空气弹簧疲劳分析［J］.力学与实践，2015，37（3）：326－331.LI Zhichao，LI Xuebing，LIU Wanqiang，et al.Fatigue Analysis of the Air Springs of the Rail Vehicles［J］.Mechanics in Engineering，2015，37（3）：326－331

［14］LEMAITRE J.A Continuous Damage Mechanics Model for Ductile Fracture［J］.Journal of Engineering Materials and Technology，1985，107（1）：83－89.

［15］TANG C Y，LEE W B.Damage Mechanics Applied to E－lastic Properties of Polymers［J］.Engineering Fracture Mechanics，1995，52（4）：717－729.

［16］MARS W V，FATEMI A.Multiaxial Fatigue of Rubber PartⅠ：Equivalence Criteria and Theoretical Aspects［J］.Fatigue ＆ Fracture of Engineering Materials ＆ Structures，2005，28（6）：515－522.

［17］MARS W V，FATEMI A.Multiaxial Fatigue of Rubber PartⅡ：Experimental Observations and Life Predictions［J］.Fatigue ＆ Fracture of Engineering Materials ＆Structures，2005，28（6）：523－538.