基于参数扰动比的高速列车车体模型修正研究

邱飞力， 张立民， 张卫华

（西南交通大学 牵引动力国家重点实验室，四川 成都610031）

高速列车整车模态的匹配影响车辆各部件结构的振动［1－2］，进而影响整个车辆系统的运行性能。目前，高速转向架空簧的非线性将导致车体垂向振动响应的频带增宽，容易引发车下质量产生共振，且抗蛇行阻抗越强将导致车体地板振动越剧烈［3］。同时，车下橡胶吊挂对车体横向减振具有积极作用，有利于车体的疲劳寿命，但过大的橡胶阻尼会使地板振动不衰减。为解决以上动力学问题，铝合金车体整体结构设计必须遵循模态匹配倍原则，与此同时，还应正确处理铝合金车体与转向架、车下橡胶吊挂参数的接口关系。进而避免车体与转向架、车下质量耦合共振，确保铝合金车体技术服役30年［4］。虽然较高的车体弯曲模态可以避免车体与转向架和车下悬挂设备间的共振，但过高的车体弯曲模态意味着较大的车体弯曲刚度，这又制约了车体的轻量化设计。在车体材料和质量一定的条件下，要保证车体的弯曲刚度需要从动态设计的角度去修改其截面形状和结构形式［5］。

不论是整车模态的匹配规划，还是轻量化车体的弯曲刚度设计，都必须先从铝合金车体结构优化入手。确定铝合金车体的模态，才能够对整备车体模态进行准确地预测［6］。同时，从振动传递和避免共振的角度出发，铝合金车体模态参数对转向架和车下设备悬挂参数的选择以及内装地板等局部结构的设计具有重要的指导意义。

铝合金车体尺寸大且结构复杂，仅凭工程师的经验建立一个与实际完全符合的模型不可能［7］。即铝合金车体设计的有限元模型不可避免地存在误差，这将会严重影响其分析结果的正确性。目前的研究表明，模型修正可以大幅提高有限元模型的准确性［8］。

在此背景下，研究高速列车铝合金车体模型修正方法，可以为后续的车体优化设计提供准确的模型，具有工程实际应用价值。

1 修正理论

铝合金车体模型修正可分成4部分：（1）模型精度判定；（2）模型修正参数选择；（3）构造模型修正目标函数；（4）模型修正的优化求解。

1.1 模型精度判定

在一定频段范围内，车体试验n阶模态参数为有限元m阶模态参数为｛f1，f2，…，fm；Φ1，Φ2，…，Φm｝。模型修正前，需要搜索出对应的试验模态和有限元模态，即模型匹配。

模态振型匹配采用振型相关性系数MAC比对，振型相关性的计算方法为［9］

式中：i、j分别为试验模态和有限元模态的阶数。

由于测试自由度不足，高阶振型无法与低阶同类振型有效区分。为此，引入频率相对误差ri，j，其计算式为

取频率误差限值为10%，匹配准则为

若式（3）成立，表明对应的试验模态与有限元模态匹配；否则，对应的试验模态与有限元模态不匹配。

为满足工程应用，频率精度目标R0取2%，振型相关性目标MAC0取0.9，建立模型精度判别式

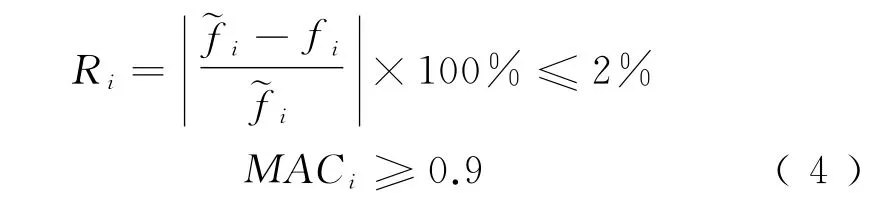
式中：Ri、MACi分别为匹配后的第i对试验模态与有限元模态间的频率相对误差和振型相关性。

1.2 修正参数选择

计算模态频率和振型MAC值对参数p的灵敏度，传统的灵敏度计算方法为［10］

该方法难以比较不同类型参数的灵敏度，为统一参数灵敏度的量纲和量级，改善灵敏度矩阵的病态性，引入有限元模型参数扰动百分比qj，则

计算频率百分比和振型相关性MAC对参数扰动比qj的差分灵敏度矩阵S，则

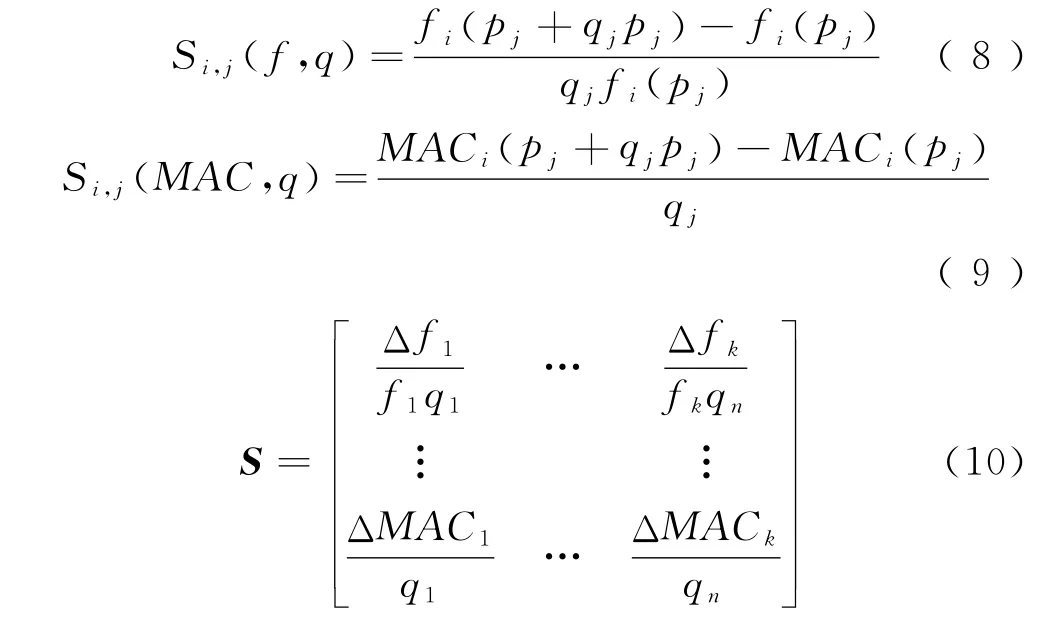
建立参数灵敏度判定准则，则

满足（11）式的参数扰动比qj选作修正变量，否则不作为修正变量，从而提高修正效率。

1.3 多目标修正函数

基于频率误差和振型MAC建立残差，则

进而建立多目标函数［11］为

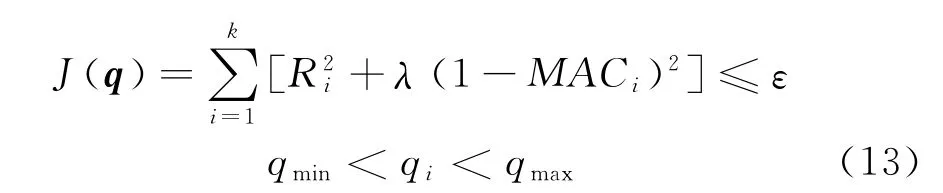
式中：ε为极小值；qmin为修正参数扰动比的下限；qmax为修正参数扰动的上限。

车体待修正模态的阶数与修正参数的数目通常不等，导致多目标函数为不适定方程组（超定或欠定）。采用传统方法求解，其结果与真实值相差极大，参数将丧失物理意义［12］。为此，引入 Tikonov正则化方法［13］求解，车体修正目标函数转换为

式中：a是正则化参数；C是正则化矩阵；d是对修正参数扰动q的限制向量；Nn为参数扰动q的集合。

1.4 正则化求解方法

正则化求解可分5步进行：

Step1 对灵敏度矩阵S作奇异值分解，并计算离散傅里叶级数的系数βi。

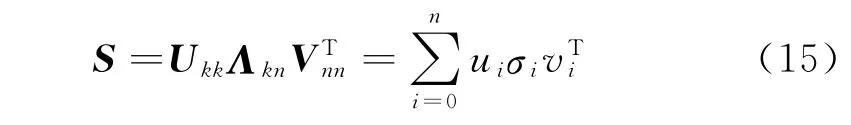
式中：矩阵U＝（u1，u2，…，uk）和Vnn＝（v1，v2，…，vn）的列向量正交；对角矩阵Λnn为奇异值矩阵，其元素满足σ1＞σ2＞…＞σn＞0。

离散傅里叶级数的系数计算为

Step2 判定线性系统Sq＝b是否满足离散Picard条件，即系统离散傅里叶级数的系数βi趋于零的速度是否快于矩阵S的奇异值σi趋于0的速度。

Step3 推导目标函数关于正则化参数a的最小二乘解表达式

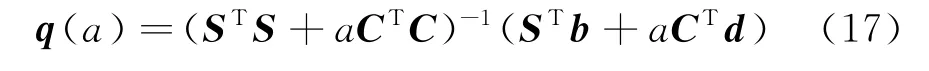
Step4 应用L－曲线法，求取正则化参数a。

将q（a）代入方程（14），可得到2部分残差向量

L－曲线法的表现形式为

H

ansen对L－曲线在正则化方法的应用作了深入研究，将L－曲线在对数尺度下曲线拐点（即最大曲率点）对应的a值作为最优正则化参数［13］。

令式（20）成立。

L－曲线曲率可由式（21）计算得出

式中：k（a）为L－曲线曲率，当k（a）其取最大值时，对应的a为最优正则化参数。

Step5 代入正则化参数至式（14），利用最小二乘法迭代至收敛，获取修正参数扰动比q。

2 模型精度判定

铝合金车体模态测试根据文献［14］进行，在车体上选取7个测试截面，每个截面4个测点，采用多点扫频激励。车体用4个橡胶堆在两端枕梁位置处进行弹性支撑，测点布置和测试照片分别见图1、图2。

图1 高速列车模态测点分布图

图2 高速列车车体测试照片

以车体垂弯测试工况为例，给出车体测点的综合频响函数，见图3。

图3 车体测点综合频响函数特性

在0～50Hz范围内，测试得到了车体的10阶弹

性模态（i＝1，2，…，10），并提取了对应测点的比例振型（i＝1，2，…，10）。车体的一阶菱形和一阶垂弯振型（分别对应频响函数的第二个和第三个峰值）见图4。

图4 车体一阶振型

选用壳单元Shell63对铝合金车体模型划分网格，并采用Combine14单元模拟车体橡胶堆的弹性支撑。利用车体沉浮频率，估算橡胶堆的弹性支撑刚度，有限元模型中车体沉浮频率随支撑刚度的变化见图5。

图5中水平虚线为沉浮模态频率2.93Hz，竖直虚线表示沉浮模态对应的支撑刚度值。进而估算橡胶的支撑刚度为1.02MN／m，此即为车体模型的边界约束。

图5 支撑刚度对一阶沉浮频率的影响

高速列车铝合金车体有限元模型见图6，X、Y和Z为车辆系统坐标系。

车体有限元模型主要的结构参数见表1。

表1 车体结构主要参数表

与测试模态相对应，在0～50Hz范围内，有限元分析共获取了22阶弹性模态频率fj（j＝1，2，…，22），并提取与试验测点对应的振型向量Φi（i＝1，2，…，22）。

计算试验和仿真模态振型MAC值和频率相对误差r，根据式（3）进行模态匹配，结果见表2。

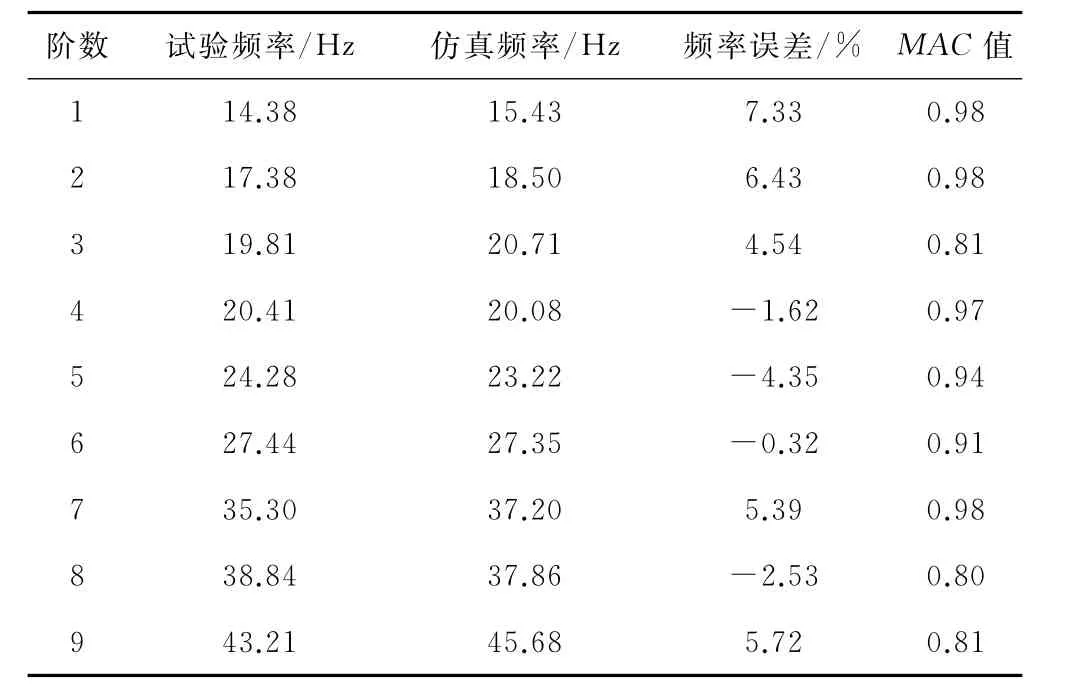
表2 模态对比表

分析表2，匹配后的仿真模态频率最大误差为7.33%，且部分MAC值不到0.9。利用车体模型精度准则判定该车体模型不满足精度要求，需要进行修正。

3 车体模型修正

3.1 修正参数选取

铝合金车体结构主要模型参数包括材料密度、弹性模量、支撑刚度以及型材尺寸等，见表3。

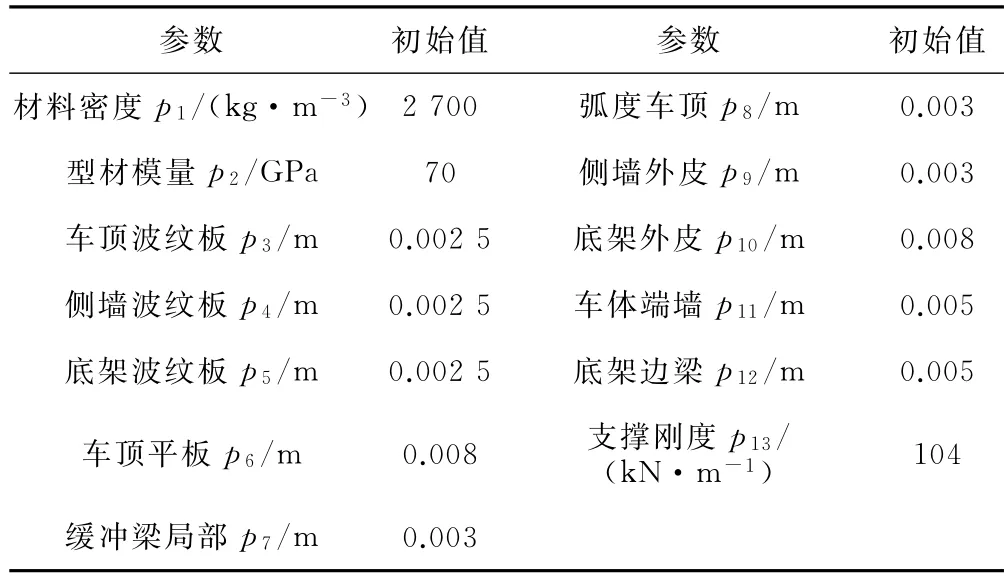
表3 车体模型主要参数及初始值

结合式（5）、式（6）计算参数的传统灵敏度矩阵，以频率灵敏度元素为例，给出其量级和单位，见表4。

表4 各类型参数灵敏度的数量级和单位

从表4知，传统的灵敏度不能衡量不同类型参数对频率的影响，无法合理选取参数。同时，灵敏度矩阵元素数量级相差甚大，其条件数Cond1＝6.591 5×1015，可见其病态性十分严重。

为此，对车体各参数作qj＝＋5%的扰动，基于式（8）～式（10）计算灵敏度矩阵S。该矩阵全部元素均为百分比，量纲统一，利于修正参数的合理选取。矩阵的条件数Cond2＝3.857 8×104，远远小于Cond1，从而大大地改善了矩阵的病态性，更利于目标函数的求解。振型相关性MAC对各参数扰动q的灵敏度，见图7（a），模态频率百分比对参数扰动的灵敏度见图7（b）。

图7 灵敏度图

由图7（a）可知，第3阶和第7阶模态振型MAC对修正参数扰动不灵敏，第8阶模态振型MAC对参数扰动灵敏度最大。由图7（b）知，密度和弹性模量扰动的灵敏度较高，模态频率百分比对参数扰动比q11～q13的灵敏度较低。

结合式（11），第3阶和第7阶振型MAC不作修正目标，参数扰动比q11～q13不参与模态频率百分比目标函数修正。以减少目标方程组维数，提高修正效率。

3.2 模型修正

将频率误差百分比和振型相关性系数取等同权重（λ＝1）；为约束参数qj趋于稳定且变化量小，C取单位矩阵I，d为零矩阵。结合式（21）求出a＝1×10－4，按照式（14）形式重写目标函数为

利用最小二乘法求解目标函数，收敛过程见图8。

图8 修正目标函数收敛图

由图8知，采用正则化灵敏度方法经过6次迭代，目标函数趋于稳定，高速列车车体模型修正完成。

修正后的有限元模态与试验模态对比见表5。

表5 修正后的模态与试验模态对比表

表5中，修正后的模态满足精度判定式（4），表明修正后的模型准确可靠。修正前后，模态频率绝对误差和振型MAC值的变化分别见图9和图10所示。

从图9、图10可知，修正后的模态频率误差得到大幅衰减；修正后模型的振型MAC得到明显的提高。

修正后的车体模型各参数改变率见图11。

图9 修正前后模态频率绝对误差

图10 修正前后振型MAC对比

图11 修正后的参数扰动比

由图11表明，各参数扰动比均在5%左右，符合实际情况。密度参数扰动比较小；型材厚度改变扰动比大部分为负值，表明初始模型尺寸较实际厚，与有限元模态频率高于测试值相吻合。

综上所述，修正后的铝合金车体模型的模态参数满足精度要求，与试验测试值相吻合。同时车体模型参数变化在±5%左右，符合车体的实际结构。这表明修正后车体模型与实际结构的预期相符合。

4 结论

通过对高速列车车体模型修正，得出以下结论：

（1）针对某铝合金车体仿真建模的不准确性，对车体有限元模型修正方法进行研究；提出了基于参数扰动比的灵敏度修正方法，并完成了该车体有限元模型的修正。修正后的结果表明该模型修正方法正确可行。

（2）修正后的车体有限元模型模态与试验测试值保持一致，车体模型各参数扰动均在允许范围内。且获取了一个与工程实际相吻合的车体有限元模型，该车体模型为后续的整车结构、转向架和车下橡胶吊挂参数的设计提供了正确的基础和依据。

（3）利用铝合金车体的实测模态频率和振型数据，首次建立了车体模型的匹配方法和模型精度判定准则，并提出了适用于车体的模型修正方法；同时，改进了模态灵敏度分析方法，统一了参数灵敏度量纲，改善了灵敏度矩阵的病态性，提高了模型修正效率。

参考文献：

［1］宫岛，周劲松，孙文静，等.高速列车弹性车体与转向架耦合振动分析［J］.交通运输工程学报，2011，11（4）：41－47.GONG Dao，ZHOU Jinsong，SUN Wenjing，ed al.Couple Vibration Analysis of Flexible Car Body and Bogie for High Speed Train［J］.Journal of Traffic and Transportation Engineering，2011，11（4）：41－47.

［2］黄彩虹，曾京，邬平波，等.铁道客车车体弹性振动减振研究［J］.工程力学，2010，27（12）：250－256.HUANG Caihong，ZENG Jing，WU Pingbo，ed al.Study on Body Flexible Vibration Reduction for Railway Passenger Carriage［J］.Engineering Mechanics，2010，27（12）：250－256.

［3］朴明伟，梁树林，方照根，等.高速转向架非线性与高铁车辆安全稳定性裕度［J］.中国铁道科学，2011，32（3）：86－92.PIAO Mingwei，LIANG Shulin，FANG Zhaogen，et al.The Non－linearity of High－speed Bogie and the Safety Stability Margin of High－speed Railway Vehicles［J］.China Railway Science，2011，32（3）：86－92.

［4］朴明伟，李明星，赵强，等.高铁车辆横向振动耦合机制及其减振技术对策［J］.振动与冲击，2015，34（3）：1－10.PIAO Mingwei，LI Mingxing，ZHAO Qiang，ed al.Lateral Vibration Coupling Mechanism of High－speed Rolling Stocks and Damping Technical Countermeasure［J］.Journal of Vibration and Shock，2015，34（3）：1－10.

［5］BEP C B，李宏.关于提高高速客车车体的弯曲刚度问题［J］.国外铁道车辆，1988（4）：24－29.BEP C B，LI Hong.The Bending Stiffness Improvement of High Speed Train［J］.Foreign Rolling Stock，1988（4）：24－29.

［6］张立民.高速列车车体模态试验技术及试验规范研究报告［R］.成都：西南交通大学，2012：58－59.

［7］朱安文，曲广吉，高耀南.结构动力模型修正技术的发展［J］.力学进展，2002，32（3）：337－347.ZHU Anwen，QU Guangji，GAO Yaonan.Processing in Model Updating for Structural Dynamic［J］.Advance in Mechanics，2002，32（3）：337－347.

［8］孙正华，李兆霞，韩晓林.大跨桥梁索塔有限元模型修正［J］.工程抗震与加固改造，2006，28（1）：50－56.SUN Zhenghua，LI Zhaoxia，HAN Xiaolin.Finite Element Model Updating for the Tower of Long－span Bridges［J］.Earthquake Resistant Engineering and Retrofitting，2006，28（1）：50－56.

［9］EWINS D J.Model Validation：Correlation for Updating［J］.Sadhana，2000，25（3）：221－234.

［10］戴航，袁爱民.基于灵敏度分析的结构模型修正［M］.北京：科学出版社，2011：54－61.

［11］邱飞力，张立民，张卫华，等.支架结构建模中设计参数的修正与优化［J］.噪声与振动控制，2014，34（1）：36－40.QIU Feili，ZHANG Limin，ZHANG Weihua，et al.Frame Finite Model Updating Based on Design Parameters Method［J］.Nosie and Vibration Control，2014，34（1）：36－40.

［12］TITURN B，FRISWELL M I.Regularization in Model Updating［J］.International Journal for Numerical Methods in Engineering，2008，75：440－478.

［13］吴颉尔.正则化方法及其在模型修正中的应用［D］.南京：南京航空航天大学，2007：22－23.

［14］中华人民共和国铁道部.TB／B3115—2005机车车辆动力学性能台架试验方法［S］.北京：中国铁道出版社，2005.