考虑通售席位的旅客列车票额优化方法

骆泳吉， 刘 军， 赖晴鹰

（北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044）

收益管理起源于美国航空业，研究如何将易逝性产品在合适的时间以合适的价格销售给合适的顾客以实现收益最大化的方法。近年来，有关收益管理的理论研究从单区段问题到多区段问题，从确定性需求到不确定需求，均得到显著发展［1］；在现实中，航空企业也受益于收益管理的应用，实现收益增长［2］。

铁路旅客运输同样存在产品易逝性，固定成本高，可变成本低等特点。因此，铁路客运运用收益管理同样具有可行性。我国铁路客运一直使用的票额分配工作也属于收益管理的研究范畴，并取得一定的成效［3－4］。针对单一票价下的席位分配问题，Ciancimino等研究在确定性需求下的DLP模型和随机需求下的PNLP模型［5］；在文献［5］的基础上，You研究两种票价等级下的铁路席位分配问题，模型考虑超售情况下的冲撞成本，由线性规划与粒子群算法相结合的优化方法快速求解［6］；钱丙益等［7］对文献［6］的模型进行扩展，考虑低价票售完后部分需求转移至高价票的buyup行为；文献［8］提出同一上车站的长短途票额嵌套模型，利用蚁群算法进行求解；文献［9］研究随机需求下的票额分配问题，通过计算客流量的期望值，将问题转化为确定性票额分配模型进行求解。

上述成果从不同角度研究铁路席位控制问题，但均未考虑铁路售票组织中常见的通售席位的设置方法。进入预售期前，有限的席位能力不仅可被分配至不同OD，还可设置为通售席位，见图1。与指定OD的票额不同，通售席位是一种共享资源，在预售期内，当某OD发生购票预定请求时，优先售出该OD的分配票额；若已分配票额售完，再使用可用的通售席位。通售席位能使票额分配方案更加灵活，在客流波动较大或客流预测不准的情况下，能起到减少客流损失的作用。

图1 结合通售席位的票额分配示意图

本文研究随机需求下，考虑通售席位的铁路旅客列车票额分配问题。首先，构建引入通售席位的票额分配随机非线性规划模型。由于需求的随机性，模型难以采用解析的方法求解。因此，主要采用抽样随机需求，模拟售票过程，进而利用样本梯度优化决策变量的思想［10］对问题进行求解。

1 考虑通售席位的票额分配模型

相比既有文献，考虑通售席位的票额优化模型引入新的决策变量，即各区间通售席位的数量。由于需求的随机性和通售席位的“先到先得”特征，使优化问题转为随机非线性规划问题，从而进一步增加模型的复杂度，模型构造为

式中：m为旅客列车停靠站数量；i、j分别为上车站、下车站序号；Z为整数集合；l为区间序号；pij为OD对（i，j）的席别票价；Cl为区间l的可售席位数量；xij为OD对（i，j）的票额分配数量；yl为区间l的通售席位数量；x＝ x1，2，…，x1，m，…，xm－2，m，xm－1，m（）为OD分配票额数量的向量；y＝ y1，y2，…，ym－1（）为区间通售席位数量的向量；fij（xij，y）为 OD对（i，j）的售票量；E fij（xij，y）［］为fij（xij，y）的期望值。

式（2）表示列车各区间的席位数应等于通过该区间的OD分配票额和该区间的通售席位数量的总和。式（3）、式（4）表示各OD分配票额及各区间通售席位数量均为不小于零的整数。

设OD对（i，j）的需求量为Dij，服从一定随机分布（均值μij，标准差σij）。由于需求的随机性，fij（xij，y）是关于xij和y的随机函数。当Dij≤xij时，该OD的票额xij可满足其需求，则有fij（xij，y）＝Dij；当Dij＞xij时，已分配票额不足以满足其需求，需额外占用相应区间的通售席位yl，l＝i～j－1。然而，通售席位属于“共用”资源，可被其余OD需求以“先到先得”的方式售出。因此fij（xij，y）受xij、y 和其余OD需求量及购票时间先后顺序的综合影响，使得E fij（xij，y）［］难以用解析式方法直接求解。本文拟通过对随机需求进行采样，利用随机样本的梯度，迭代优化决策变量x和y。

2 基于随机梯度算法的求解步骤

首先，将原问题（P0）转换为确定性需求下的资源分配问题，求初始可行解。在此基础上，通过采样随机需求，生成样本路径，模拟计算样本的一阶差分，利用随机梯度算法，迭代优化决策变量，具体步骤为：

Step1 设置初始可行解x0（）和y0（）

将各OD随机需求简化为确定性需求，即Dij＝E设定能力分配比例参数0＜θ＜1，将原问题简化为确定性线性规划问题DLP（Deterministic Linear Programming），即

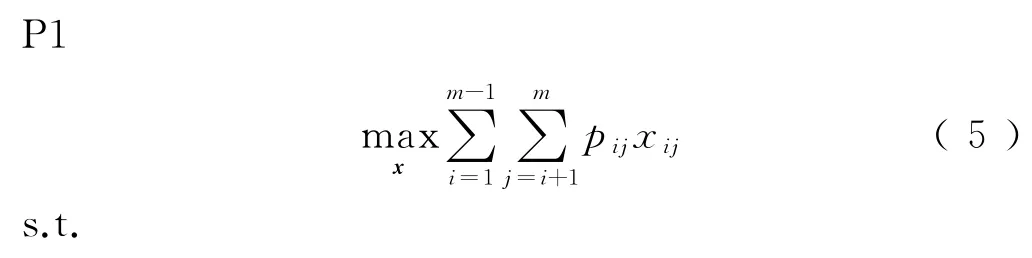
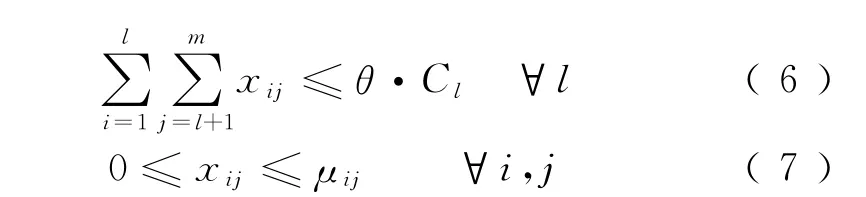
式中：μij为OD对（i，j）的平均需求量。式（6）表示OD分配票额不应超过可分配的能力；式（7）表示各OD分配票额不应大于μij。

设迭代次数k＝0，向下取整（P1）的最优解，得到x的初始可行解为

已知x0（），y0（）由下式可得（i，j）的累计购票数量。

需求序列ws的购票过程描述为：当购票需求ws，t＝（i，j）到达时，若（i，j）的票额充足，即xij，t≥1，则令qij，t＋1＝qij，t＋1，xij，t＋1＝xij，t－1；若 （i，j）的分配票额不足，即xij，t＜0，但对应区间有可用的通售席位，即l＝i，…，j－1，有yl，t≥1，则令qij，t＋1＝qij，t＋1，yl，t＋1＝yl，t－1（l＝i，…，j－1）；若 （i，j）的分配票额和相应区间通售席位均不足，即xij，t＝0且-l＝i，…，j－1，有yl，t＜1，则该需求购票失败，各变量无变化。

模拟需求序列ws的售票过程，计算样本收益针对xij的一阶差分为

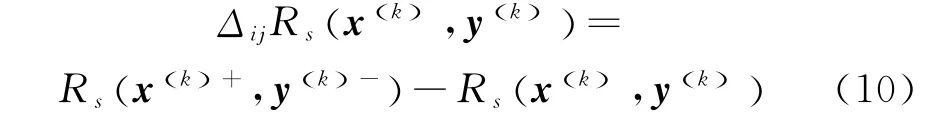
式中：Rsxk（），yk（）（）为ws在决策变量xk（）和yk（）下的列车总收益；xk（）＋为在xk（）基础上单位增加OD （i，j）票额 （其余 OD 不变）后的新决策变量；yk（）－为在yk（）基础上单位减少区间l＝i～j－1通售席位数量（其余区间不变）后的新决策变量；ΔijRsxk（），yk（）（）为决策变量变化前后的列车收益差。若xk（）＋、yk（）－不在可行域内，则令ΔijRsxk（），yk（）（）＝0。

Step2 近似计算随机样本梯度

由于购票过程具有随机性，列车收益难以用解析方法表达。因此，参照文献［10］对离散问题的梯度处理思想，用随机样本一阶差分近似列车收益对于决策变量的梯度。

首先，设置随机采样数量n，根据OD需求的概率分布和实际购票时间分布，随机生成购票需求序列ws，s＝1，2，…，n。设ws，t为ws中的第t个购票需求的二元组，记录该需求的上车站、下车站序号；xij，t、yl，t分别为第t个需求到达前 OD对（i，j）的票额和区间l的通售席位数量；qij，t为第t个需求到达前OD对

计算所有样本的一阶差分的期望值，近似求得总收益关于xij的梯度

式中：n为随机采样总数。

Step3 优化OD分配票额xk（）和区间通售席位数量yk（）

设ρk（）为第k次迭代时的步长，则为xij更新后的位置。由于＝不一定在可行域内，首先计算在连续可行域内的正交投影

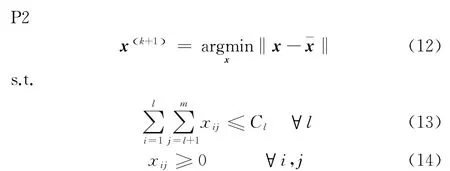
取整x （k＋1）＝"x （k＋1）#，对y （k＋1）更新为

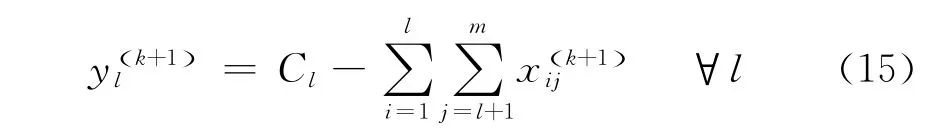
Step4 检测迭代终止条件

若‖x （k＋1）－xk（）‖／‖xk（）‖＜ε或k＝kmax时，终止迭代，x（k＋1）、y（k＋1）为最终解；否则，令k＝k＋1，返回步骤2。

3 实例

以2013－08－01～2013－08－31上海虹桥开往北京南的G102次列车二等座为例，列车共有m＝8个停车站，见图2。以周末（周五～周日）客流数据为基础，统计OD均值和标准差。表1为OD的票价、需求均值、需求标准差的三元组。

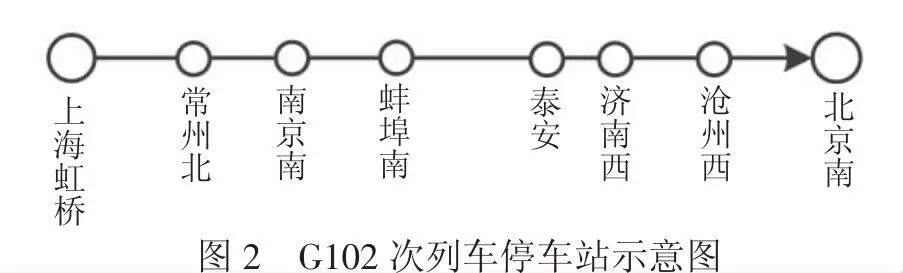
图2 G102次列车停车站示意图

设列车定员为650人，OD分配票额初始分配比例θ＝0.8，迭代中的随机采样数量n＝20；与文献［5－7］中铁路需求量的随机分布相同，假设OD需求总量服从正态分布，需求序列中不同OD的购票顺序根据历史购票时间分布生成；设迭代步长随迭代次数递减，即ρ（k）＝0.2／，迭代终止系数ε＝0.01，最大迭代次数kmax＝500。采用Matlab编程实现，线性规划问题（P1）和二次规划问题（P2）可分别用优化函数linprog、quadprog快速求解。

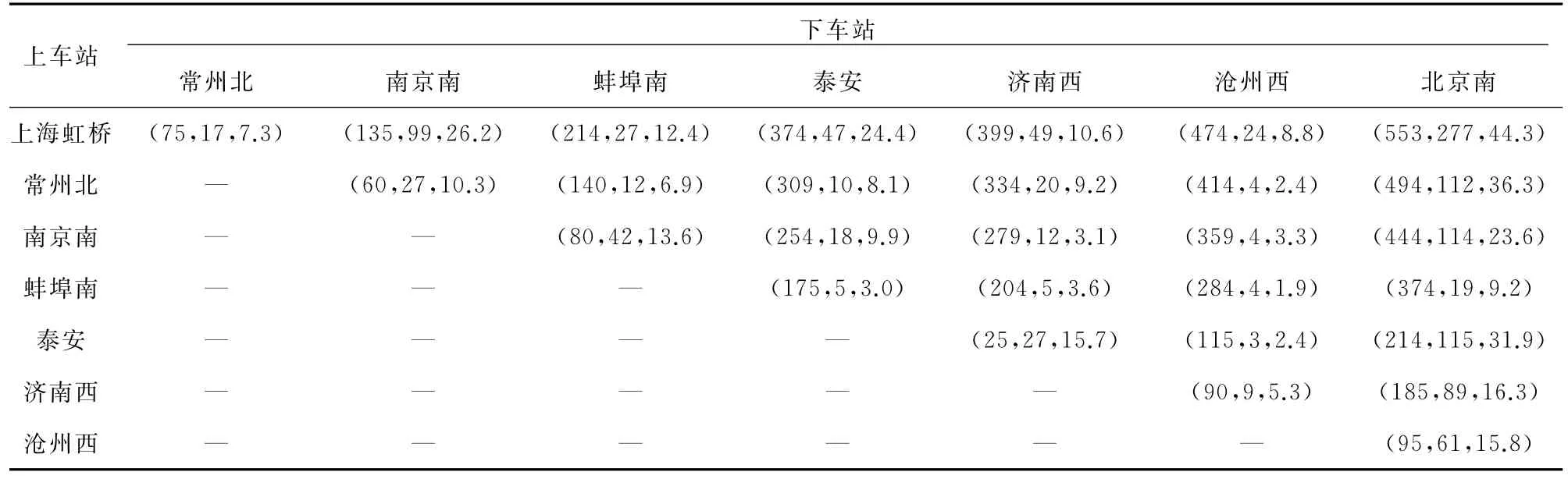
表1 价格、需求均值、标准差 （元，人，人）

首先，采用确定性线性规划模型（DLP）求解无通售席位的票额分配方案，即令θ＝1，求解式（5）～式（7），分配结果见表2。设随机测试样本数量N＝50，针对随机需求序列ws，模拟在该票额分配方案下的售票过程，计算仿真总收益r （ws），统计平均仿真总收益／N＝33.25万元 。

使用本文提出的优化方法求解考虑通售席位的票额分配方案，迭代过程见图3，分配结果见表3、表4，平均仿真总收益为34.29万元，相比无通售席位的DLP模型提高3.14%。

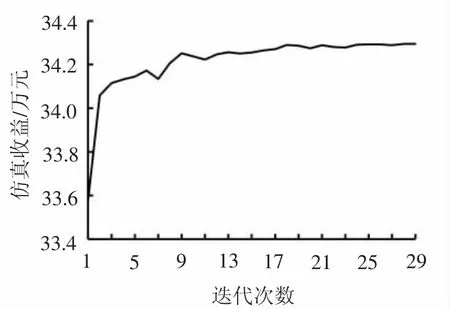
图3 迭代优化过程

表2 无通售席位的DLP求解方案 张

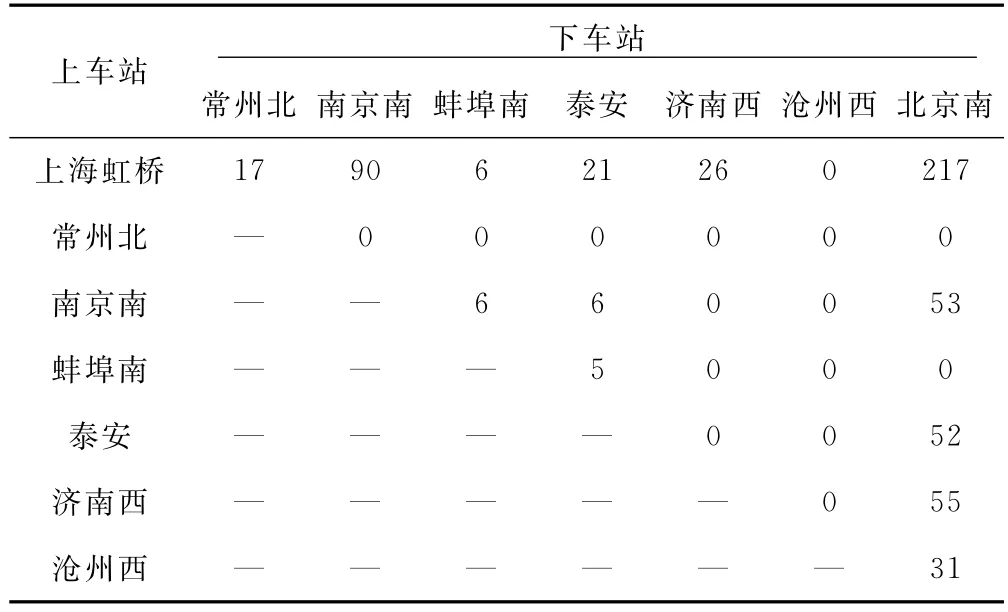
表3 考虑通售席位的OD分配票额数量 张

表4 区间通售席位数量 张

4 结论

当需求具有较强的随机性时，引入通售席位的票额分配方法使分配方案更加灵活，相比经典的DLP模型，收益有一定程度的提高。但是，数据成本方面，本文算法需要统计旅客历史购票时间的分布，作为样本采样的基础，数据成本更高；计算成本方面，随着随机采样数量增多，虽然能使梯度的估计值越准确，但计算效率更低，相比无须随机采样的DLP模型更为耗时。通过不同需求数据下的反复试验，可以发现模型的优化结果依赖于初始分配比例参数θ，即算法不保证能够收敛于全局最优解。尽管如此，优化算法能使票额分配方案总体上向列车收益上升方向更新，在实际应用中具有一定的价值。

参考文献：

［1］TALLURI K T，VAN RYZIN G J.The Theory and Prac－tice of Revenue Management［M］.USA：Kluwer Academic Publishers，2004：27－127.

［2］SMITH B C，LEIMKUHLER J F，DARROW R M.Yield Management at American Airlines［J］.Interfaces，1992，22（1）：8－31.

［3］单杏花.铁路客运收益管理模型及应用研究［D］.北京：中国铁道科学研究院，2012：102－129.

［4］王洪业，吕晓艳，周亮瑾，等.基于客流预测的铁路旅客列车票额智能分配方法［J］.中国铁道科学，2013，34（3）：128－132.WANG Hongye，LV Xiaoyan，ZHOU Liangjin，et al.Intelligent Seat Allotment Method for Railway Passenger Train Based on Passenger Flow Forecast［J］.China Railway Science，2013，34（3）：128－132.

［5］CIANCIMINO A，INZERILLO G，LUCIDI S，et al.A Mathematical Programming Approach for the Solution of the Railway Yield Management Problem［J］.Transportation Science，1999，33（2）：168－181.

［6］YOU P.An Efficient Computational Approach for Railway Booking Problems［J］.European Journal of Operational Research，2008，185（2）：811－824.

［7］钱丙益，帅斌，陈崇双，等.基于旅客buy－up行为的铁路客运专线收益管理模型［J］.铁道学报，2013，35（8）：10－15.QIAN Bingyi，SHUAI Bin，CHEN Chongshuang，et al.Revenue Management Model for Dedicated Passenger Line Based on Passengers’Buy－up Behavior［J］.Journal of the China Railway Society，2013，35（8）：10－15.

［8］包云，刘军，马敏书，等.高速铁路嵌套式票额分配方法研究［J］.铁道学报，2014，36（8）：1－6.BAO Yun，LIU Jun，MA Minshu，et al.Nested Seat Inventory Control Approach for High－speed trains［J］.Journal of the China Railway Society，2014，36（8）：1－6.

［9］包云，刘军，刘江川，等.基于随机需求的单列车票额分配方法［J］.中国铁道科学，2015，36（2）：96－102.BAO Yun，LIU Jun，LIU Jiangchuan，et al.Seat Allotment Method for Single Train Based on Stochastic Demand［J］.China Railway Science，2015，36（2）：96－102.

［10］BERTSIMAS D，DE BOER S.Simulation－based Booking Limits for Airline Revenue Management［J］.Operations Research，2005，53（1）：90－106.