基于时延自相关ICA的列车轮对轴承复合故障诊断方法

黄采伦， 李 忠， 王 靖， 张小娟， 曾照福

（1.湖南科技大学 信息与电气工程学院，湖南 湘潭 411201；2.湖南省矿山安全预警技术与装备工程实验室，湖南 湘潭 411201）

轮对轴承是列车走行部的重要部件，由于其长期工作在恶劣环境及高速重载状态，工作面极易产生疲劳、麻点、碾皮、擦伤、烧附、腐蚀、凹痕、裂损、碰伤等故障，且这类故障存在多发性、复合性［1］。一旦发生故障，可能导致列车晚点、中途停车，甚至威胁列车安全等。因此轮对轴承工作状态的好坏直接影响到列车的安全运行。

常见的列车轮对运行状态监测与故障诊断方法有共振解调法、特征谱分析法、离散余弦包络分析法等［2－3］，这些方法在列车轮对的早期故障、单一故障诊断方面取得了较好的应用效果，但在轮对复合故障诊断时因为轮对复合故障信号的各故障源之间存在耦合与调制，故障特征十分复杂，不易辨识［4］，因此常出现误诊。对复合故障的准确诊断是机械故障诊断研究的一个重要方面，常用的方法有小波变换、经验模态分解等。文献［5］采用高密度小波变换与包络谱相结合的方法对具有早期复合故障的轴承进行诊断；文献［6］运用遗传算法对存在多个故障的滚动轴承实现了有效诊断。但是这些方法没有考虑各故障源之间或故障源与噪声信号之间的关系，所以并不能将各个故障特征分离开来。如果将复合故障信号解耦为N个互不相关的故障源信号，就可以有效提高故障诊断的精度，独立分量分析（Independent Component Analysis，ICA）是基于这一思路产生。

ICA常用于盲分离平稳、非平稳信号的干扰源，可用于非高斯信号的处理和提取优良的故障特征，故可将ICA技术用于存在复合故障的列车轮对轴承监测信号盲分离［7－9］。时延自相关处理不需要任何关于信号与噪声的谱分布、概率分布的先验知识，能有效降低信号中的噪声［10－11］；由于列车轮对状态监测中存在强背景噪声，并且现场振动情况十分复杂，运用时延自相关处理方法可有效提高监测信号的信噪比。本文将时延自相关降噪与ICA相结合提取并分离列车轮对轴承复合故障的特征信息，仿真分析与实际应用结果均表明，该方法能有效诊断列车轮对轴承复合故障。

1 时延自相关降噪

ICA的很多算法是在未考虑噪声的模型下推导出来［12］。由于列车轮对运行环境恶劣，且存在着诸多因素的干扰，故在列车轮对故障诊断系统中，传感器采集到的振动信号不可避免地受到噪声的影响。因此，在对振动监测信号进行ICA处理之前，要先进行降噪，以提高信噪比。小波降噪是一种比较成熟而有效的方法，但该方法需要设置阈值，如果阈值设置不当，就有可能将信号中有用的微弱信号去除，从而导致误诊。时延自相关降噪方法因不需要任何关于信号与噪声的先验知识，且在降噪时不会丢失信号的有用成分，在设备状态监测中得到广泛应用。

自相关函数［10］描述的是同一信号在不同时刻t、t＋τ的相互关联紧密性，其定义为

式中：T表示信号周期；τ表示时延。

根据式（1）可得列车轮对振动监测信号的离散自相关函数表达式为

式中：N为采样点数；x i（）等价于x （iΔt）＝x t（），是振动信号样本函数；Rxxk（）等价于Rxx（kΔt）＝Rxxτ（），τ为时间坐标移动值，Δt为采样间隔。

式（1）、式（2）表示的自相关函数具以下性质：

（1）当τ＝0时，自相关函数值最大；

（2）当τ趋于无穷大时，随机振动信号的自相关函数值将趋于0或某一常数值；

（3）周期分量的自相关函数仍保持原来的周期性而不衰减。

因此，在列车轮对振动监测中，可利用自相关函数进行信号降噪，从而保留振动信号中周期性的有用信号，去除随机的非周期性高斯白噪声。

2 ICA

2.1 ICA原理

ICA是盲信号处理的一种，它是指在未知源信号及源信号传输混合通道特性等的情况下，仅由传感器检测信号估计或分离出各个独立源信号的过程。最典型的例子是“鸡尾酒会”问题［7］，仅根据多个麦克风拾取到的信号分离出各个语音信号。假设M 个源信号为

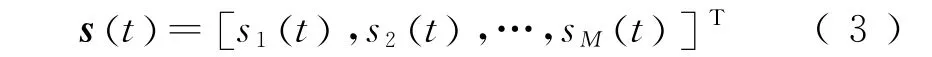
N个传感器获得的监测信号为

噪声信号为

用A表示未知的混合系数矩阵，则噪声环境下的ICA基本数学模型可以简单表示为

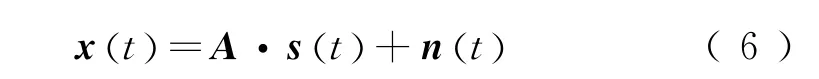
那么ICA的目标就是找到一个分离矩阵W，通过式（7）所示的变换对监测信号x（t）进行分离，使得分离信号y（t）是对源信号s（t）的最优估计。

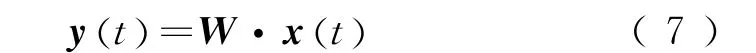
2.2 基于负熵的快速ICA算法

由概率论的中心极限定理可知，在一定条件下，一组独立随机变量的和比原始随机变量中的任何一个更趋向于高斯分布。概率论已经证明负熵可以作为非高斯性的度量。因此，如果能对混合信号的非高斯性最大化就可将信号分离。设随机向量y的概率密度为ρ（y），则向量y的熵可定义为

为了让对高斯分布变量的“熵”为零且总是非负，定义熵的一种新形式，叫负熵。负熵J定义为

显然，高斯随机变量的负熵为零。由信息论知识可知，高斯变量的熵最大，故负熵总是非负的。

由于使用负熵的定义来计算负熵比较困难，Hyvrinen用最大熵原理近似负熵［9］，表达式为

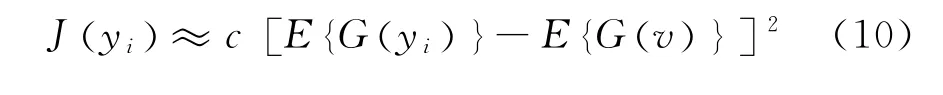
式中：c为常数；E为数学期望；G为任意非二次函数；v为一标准化的高斯变量；变量yi为标准化的随机变量。算法通过最大化函数

来找到一个独立分量yi＝wTx。这里w为m维向量且满足约束条件

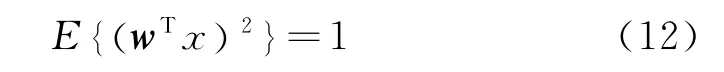
根据不同类型信号的特点以及对算法的要求，函数G的选择在文献［9］中有较为详细的介绍。

快速ICA算法的核心在于通过一个学习规则找到一个单位权值向量w，使得投影wTx非高斯性最大化，非高斯性的评判尺度是由负熵的估计J （wTx）给出。快速ICA算法的程序框图见图1。

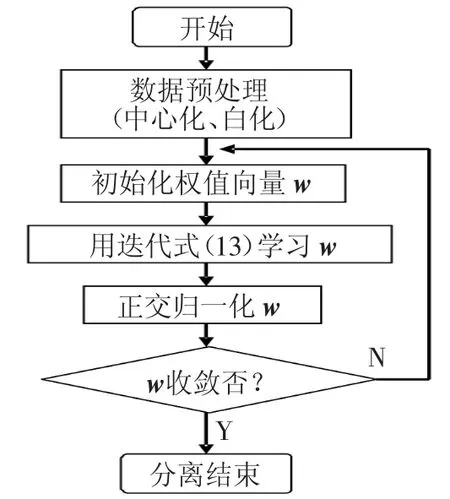
图1 快速ICA算法流程

算法的迭代式为

式中：函数g是非线性函数G的导数。当n个独立分量估计出来时，得到n个w1、w2、…、wn，从而得到分离矩阵W。

3 MATLAB仿真分析

根据列车轮对轴承的结构特点，当外圈发生损伤故障时，主要产生脉冲调制现象；由于受到轴承系统阻尼因素的影响，系统固有简谐振动信号x（t）以类似于指数衰减的形式存在，信号的能量逐渐减弱，用式表示为

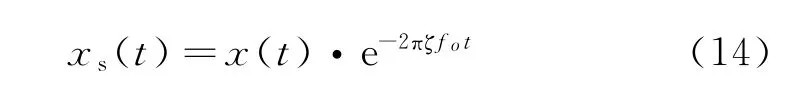
故障冲击信号可以表示为

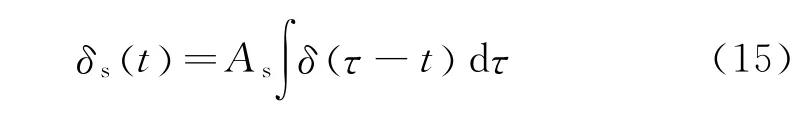
式中：As表示冲击信号的强度；ζ为阻尼系数；fo为外圈故障特征频率。所以外圈故障冲击信号δs（t）与系统固有简谐衰减振动信号xs（t）之间的脉冲调制响应为自由衰减振动，其输出响应为

式中：fm为轴承系统固有振动频率；θ为初始相位；A为振动幅值。

当轴箱轴承滚动体发生损伤故障时，主要是滚动体故障冲击振动xb（t）与滚动体公转振动xc（t）之间产生的振幅调制现象。其输出响应为

当轴箱轴承内圈发生损伤故障时，主要是内圈的故障冲击振动xi（t）与车轴旋转振动xz（t）、滚动体公转振动xc（t）发生的振幅调制现象。其输出响应为

式中：fb为滚动体故障特征频率；fc为滚动体公转频率；fi为内圈故障特征频率；fz为车轴转动频率；am、θm分别为滚动体公转振动的第m阶谐波分量的幅值、相位；an、θn分别为滚动体故障冲击振动的第n阶谐波分量的幅值、相位；ak、θk分别为内圈故障冲击振动的第k阶谐波分量的幅值、相位；al、θl分别为车轴旋转振动的第l阶谐波分量的幅值、相位。

图2 轮对轴承故障信号仿真

以DF4B型内燃机车的轮对轴承（型号为552732QT）为例，在列车速度为120km／h，轴频为8.488Hz时，根据轴承几何参数可计算出内圈、外圈、滚动体故障特征频率分别为83.226、61.075、26.996 Hz。根据式（16）～式（18）和轴承几何参数，使用MATLAB对轮对轴承的内圈、外圈、滚动体故障信号进行仿真，仿真信号及其频谱见图2。

轮对轴承安装在轴箱内部，其实际振动信号还包括列车低频振动l（t）和噪声n（t），所以对式（16）～式（18）改进可得

在列车轮对运行状态监测中，以内燃机车为例，其轮对、牵引电机等组成了一个轮对电机组装整体，通常将振动监测传感器安装在轮对轴箱外壳、牵引电机的刷端和齿端等部位。假设轮对轴承同时存在内圈、外圈、滚动体的复合故障，以下仅研究轮对轴承的复合故障诊断，未考虑电机轴承、齿轮箱的故障振动。安装在轮对轴箱外壳、牵引电机齿端、牵引电机刷端的传感器拾取到的3个故障冲击振动的综合响应为

式（20）中，根据传感器的安装位置与各故障的关系确定wij，则可由MATLAB将图2所示的内圈、外圈、滚动体故障仿真信号合成为图3所示的传感器监测信号。由图3可看出，轴承故障特征信息基本上湮没在噪声中，无论从时域或频域都无法识别出故障。

对图3中的信号进行时延自相关降噪后得到的信号见图4，可见经过降噪处理后，信噪比大大提高，说明时延自相关处理在信号的降噪上有很好的效果，但故障特征信息十分微弱，且各频率成分混叠在一起，难以识别出故障。

图3 轮对轴承故障监测信号仿真

图4 自相关降噪后信号

图4中的信号经过ICA处理后见图5，复合故障信号的各独立成分实现了很好的分离，轴承的内圈、外圈、滚动体3个故障特征在图5频谱中得到很好的体现，故障特征信息十分明显。这说明，进行ICA处理能够将各个独立故障源分离开并使故障特征得到增强，通过对信号的ICA处理，达到了比较好的分离效果，从而可实现列车轮对轴承复合故障的准确诊断。

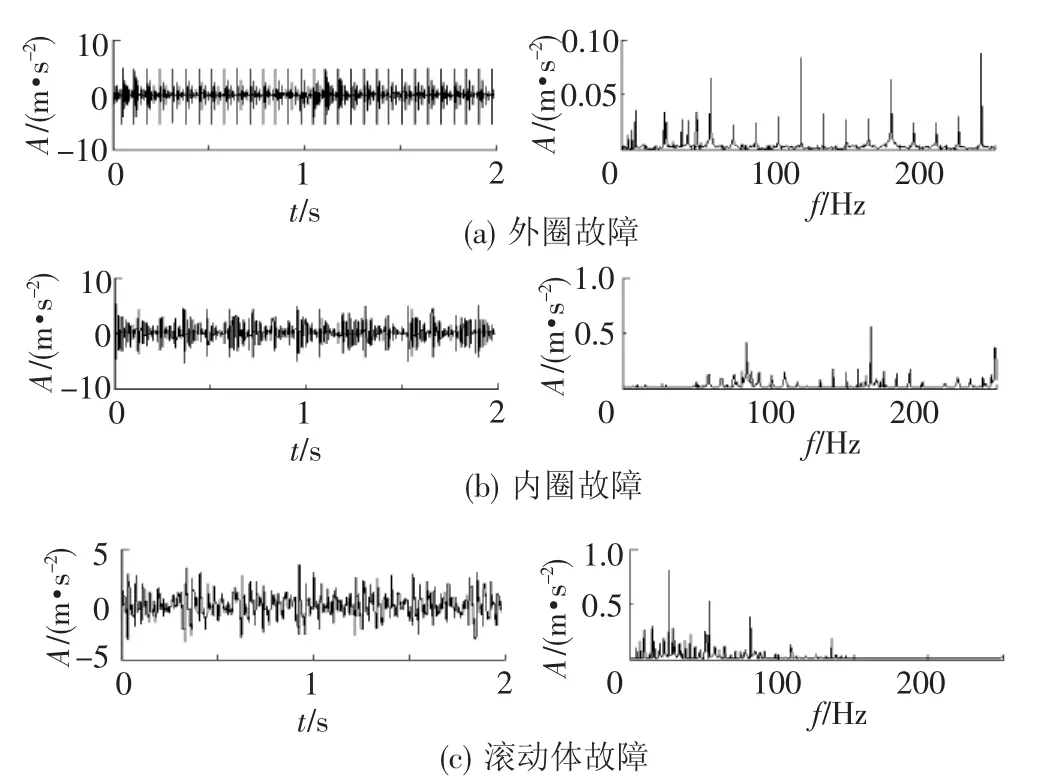
图5 ICA分离后信号

4 轮对轴承复合故障诊断实例分析

图6为课题组研制的“机车走行部故障在线诊断系统”在某DF4B型内燃机车上的一组监测数据，分别在轮对轴箱、电机齿端、电机刷端处安装3个振动加速度传感器，对型号为552732QT的轮对轴承进行在线状态监测。数据采集时的列车速度为96km／h，采样频率为512Hz，采样点数为2 048个。

由轴承参数可计算出采集时刻内圈、外圈、滚动体故障特征频率分别为66.581、48.860、21.597Hz。由图6可知，各传感器的监测信号非常复杂，包含了大量背景噪声，其频率成分十分丰富，轴承故障特征信息被大量背景噪声所淹没，很难确诊是否存在故障。

图6 列车轮对在线监测信号

对比图6、图7，可以看出经过时延自相关降噪处理后，信号中的非周期成分得到消除，只留下了与故障信息等有关的周期成分，噪声得到了有效的抑制，大大提高了信噪比。虽然从图7频谱图可以看到存在一些故障特征谱线，但是各频率成分存在一定程度的混叠，不易区分故障具体位置。

图7 降噪处理后的图6信号

经过时延自相关降噪后的信号，去除了其中的非周期成分，保留了信号中具有周期性的故障特征信息，然后对信号进行盲分离，就可以对轴承故障特征进行提取，图8为经过ICA分离后得到的3个分离信号及其频谱。从图8（a）和图8（c）可看出，轴承的内圈故障频率和外圈故障频率实现了很好的分离，故障特征得到明显增强。从频谱上可以明显找出66.6、48.9Hz的故障特征谱线，这与前面计算所得的内圈、外圈故障特征频率基本一致，因此可以确诊被监测轴承存在内圈、外圈缺陷的复合故障。图8（b）表示分离后得到的其他信号。

图8 ICA分离信号

经机务段技术人员对多次转储数据分析并确认故障存在后扣车分解该轴箱检查发现：轴承的内圈、外圈均存在缺陷，故障图片见图9。

图9 监测轴承故障部位

诊断结果表明论文所述方法能够有效的将各个独立故障源分离出来，在列车轮对轴承故障信号的分离及故障特征的提取上具有良好的效果。一般的信号盲分离都是直接对混合信号进行处理，往往难以达到较为满意的效果。对于运行在恶劣环境下的列车轮对轴承，如果出现复合故障，传感器拾取到的振动冲击信号非常复杂，需首先进行降噪处理，才能达到较好的ICA分离效果。

5 结论

针对列车运行环境下传感器拾取到的列车轮对轴承振动信号具有强烈的背景噪声，以及快速ICA算法在含噪条件下信号分离效果不佳的特点，论文将独立分量分析与时延自相关降噪相结合，首先对采集信号进行时延自相关处理，消除大量非周期性的噪声成分，然后对降噪处理后的信号进行盲分离。仿真与实例分析均表明，独立分量分析方法在列车轮对轴承复合故障振动冲击信号的分离应用上是有效可行的，能够简化故障分类，便于复合故障的分析与诊断。仿真与实际诊断结果充分表明了论文所述方法的正确有效性，说明独立分量分析与时延自相关降噪相结合的方法在列车轮对轴承故障诊断上具有很好的应用性，也可以用于其他类型的旋转机械故障诊断。

参考文献：

［1］黄采伦，樊晓平，陈特放.列车故障在线诊断技术及应用［M］.北京：国防工业出版社，2006：23－161.

［2］高立新，王大鹏，刘保华，等.轴承故障诊断中共振解调技术的应用研究［J］.北京工业大学学报，2007，33（1）：1－5.GAO Lixin，WANG Dapeng，LIU Baohua，et al.Study on Application of Resonance－demodulation Technology in Rolling Bearing Fault Diagnosis［J］.Journal of Beijing University of Technology，2007，33（1）：1－5.

［3］黄采伦，樊晓平，陈春阳，等.基于小波系数提取及离散余弦包络分析的机车牵引齿轮故障诊断方法［J］.铁道学报，2008，30（2）：98－102.HUANG Cailun，FAN Xiaoping，CHEN Chunyang，et al.Fault Diagnosis Method of Locomotive Driven Gear Based on Envelopment Analysis of Wavelet Coefficients Extraction and DCT［J］.Journal of the China Railway Society，2008，30（2）：98－102.

［4］李红芳，张清华，谢克明.旋转机械的并发故障诊断技术研究进展［J］.噪声与振动控制，2008，28（3）：67－70.LI Hongfang，ZHANG Qinghua，XIE Keming.Research Progress on the Composite Fault Diagnosis Technology of Rotary Machine［J］.Noise and Vibration Control，2008，28（3）：67－70.

［5］秦毅，王腾，何启源，等.高密度小波变换在滚动轴承复合故障诊断中的应用［J］.重庆大学学报，2013，36（3）：13－19.QIN Yi，WANG Teng，HE Qiyuan，et al.Application of Higher Density Wavelet Transform to Composite Fault Diagnosis of Rolling Bearing［J］.Journal of Chongqing University，2013，36（3）：13－19.

［6］骆志高，陈保磊，庞朝利，等.基于遗传算法的滚动轴承复合故障诊断研究［J］.振动与冲击，2010，29（6）：174－177.LUO Zhigao，CHEN Baolei，PANG Chaoli，et al.Rolling Bearing Complex Fault Diagnosis Based on Genetic Algorithm［J］.Journal of Vibration and Shock，2010，29（6）：174－177.

［7］陈晓军，成昊，唐斌.基于ICA的雷达信号欠定盲分离算法［J］.电子与信息学报，2010，32（4）：919－924.CHEN Xiaojun，CHENG Hao，TANG Bin.Underdetermined Blind Radar Signal Separation Based on ICA［J］.Journal of Electronics ＆Information Technology，2010，32（4）：919－924.

［8］BARELLA S，BELLOGINI M.BONIARDI M，et al.Failure Analysis of a Steam Turbine Rotor［J］.Engineering Failure Analysis，2011，18（6）：1 511－1 519.

［9］Aapo Hyvrinen.Fast and Robust Fixed－point Algorithms for Independent Component Analysis［J］.IEEE Trans on Neural Networks，1999，10（3）：626－634.

［10］孟涛，廖明夫，李辉.利用时延相关解调法诊断滚动轴承的故障［J］.航空学报，2004，25（1）：41－44.MENG Tao，LIAO Mingfu，LI Hui.Detection and Diagnosis of the Rolling Element Bearing Fault by the Delayed Correlation－envelope Technique［J］.Acta Aeronautica et Astronautica Sinica，2004，25（1）：41－44.