简述初中数学数形结合教学策略

鄢玲

【摘要】 初中是学生学习数学的关键阶段之一，相对于小学数学的内容，初中数学难度增加，知识范围也更大，学好初中数学也是学习高中数学的基础. 对于初中生来说，选择正确的学习方法，能够有效培养数学学习能力和数学思维. 对于初中数学教师来说，可以适当的运用数形结合的方式开展教学. 本文将就初中数学数形结合教学策略展开探讨.

【关键词】 初中数学；教学方法；数形结合

引言：数学是一门逻辑性较强的学科，数学研究的主要内容是空间形态和数量关系等，数学学科包括了数和形两个大概念，要提高解题速度和解题正确率，就要将数和形两个概念恰当的结合起来，教学中也要将数形结合作为一种重要的方法传授给学生.

1. 数形结合思想简介

从字面上看，数形结合就是将图形和数量结合起来，运用其中的关系解决问题，将抽象和复杂的数量转化为具体和简单的图形，这样更加直观和形象，便于解决问题. 一些题目也需要把数量关系转化为图形来分析和解决，数形结合思想的核心就是数量和图形的相互转化. 在初中阶段，学生的抽象思维还不是很强，因此运用数形结合的思想解决问题是一种非常重要的方式，也能够培养学生的数学思维能力，最重要的就是变抽象为具体，变繁琐为简单，提高解题效率和正确率，帮助学生树立学好数学的信心，消除对数学的厌烦和畏惧心理，提高数学成绩，对于教师提高课堂教学效率也有很大帮助.

2. 数形结合思想的重要作用

数学是一门抽象性较强的学科，并且还有形式化和符号化的特点，理解数学知识和概念可能存在一定难度，再加上解决数学问题一般需要复杂的逻辑推理，因此很多学生不喜欢数学甚至厌烦和恐惧. 而教师一般只是传授理论知识，对于学生是否听懂、是否能够解题不甚了解，反复强调单一的逻辑思维，却不运用图形的方法帮助学生更好的理解抽象的数学概念. 实际上教材中就包含了大量的数形结合思想，在教学过程中教师可以恰当的运用，揭示数学的本质，减轻学生学习数学的负担.

3. 数形结合思想在初中数学中的应用

3.1 以数化形的应用

在初中数学中，一些数学知识和数学关系较为抽象，学生理解可能存在一定困难，而图像能够形象、直观的表达信息，可以将抽象的关系、知识变得具体. 在初中阶段，以图形来代替数量主要有两种方法，也就是采用平面几何或者解析几何的方式. 以数化形的优点是：采用简单直观的数学图形，不需要大量的计算或者推理，更容易理解数学中晦涩难懂的概念和关系，取得良好的学习成果. 例如在讲授平方差公式这一概念的时候就可以运用数形结合的方法，首先计算多项式相乘：（m + 2）（m - 2）、（2x + 1）（2x - 1），得到结果后进行比较，分析两个结果与算式的关系，找到其中的规律，然后计算（a + b）（a - b），得到平方差公式，再结合图形分析平方差公式的内容，了解平方差公式的几何意义.

3.2 以形化数的应用

图形具有直观易懂的优点，但是无法表示定量，因此还要结合代数计算才能实现定量. 对于一些图形，不论是复杂的还是简单的，单单靠观察可能很难找到规律或者得到结论，因此还要结合数量来分析，挖掘图形中包含的隐含条件，利用数量关系解决图形问题. 例如在讲解角平分线这部分知识时，教师首先向学生介绍平分角的仪器，引导学生使用尺规作出角平分线，然后让学生通过折纸的方式自己找出角平分线，教师应引导学生观察纸张上折痕的数量和长度，最后总结角平分线的定理和性质，但是教师仍然需要进行推理和证明.

3.3 数形互变的应用

解决一些数学问题有时单单依靠上述两种思想是不够的，需要将以形化数和以数化形两种方法结合起来. 例如在讲解函数与平面直角坐标系的知识时，教师应告诉学生坐标系除了可以表示地理位置，还可以在直角坐标系中架设一座“桥梁”，桥梁上的每一点都与平面上的有序数对（x，y）对应，将函数与直角坐标系结合起来.

3.4 数形结合思想在函数中的应用

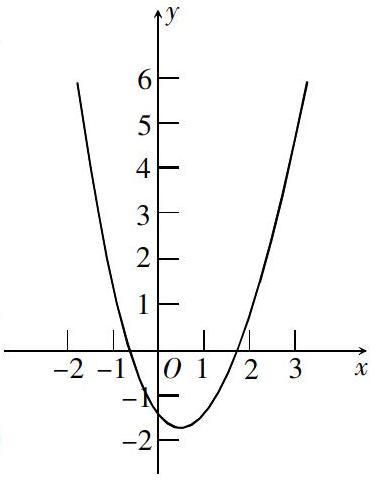
初中数学中函数是重点内容也是难点之一，其中的二次函数是学习高级数学的基础，因此采取数形结合的思想进行学习是非常重要的. 例如：如果关于x的方程x2 + 2kx + 3k = 0有两根，并且都在3和-1之间，那么k的取值范围是多少？对于这道函数问题，可以设f（x） = x2 + 2kx + 3k，结合下面的图像 ：

可得f（-1） > 0，f（3） > 0，f（-k） < = 0，也就是2（-1） + 2k（-1） + 3k > 0，32 + 2k·3+3k > 0，（-k）2 + 2k（-k） + 3k < =0，可以解得k > =3或-1 < k < = 0.

3.5 数形结合思想在应用题中的应用

应用题分值较高，考察的是学生的综合能力，学生解决问题时可能会遇到困难，在应用题中采用数形结合的方法解题，能够大大提高解题效率，提高解题正确率. 例如：一公司生产新产品，推销数量为x，推销费用为y，根据下图回答问题：（1）y1和y2的解析式为？（2）图中两种方案如何付推销费？

解：（1）解析式为：y1 = 20x；y2 = 300 + 10x；（2）y1不需要推销因此无推销费，推销十件可得推销费200元；而y2有300元保底工资，推销十件可得100元提成.

结束语

综上，在初中数学中不论是教学还是学习，都渗透着数形结合的思想，恰当的运用这种思想，能够提高解题效率和正确率，改善教学效果.