“翻转课堂”理念下教师应具备的数学教学技能
2016-05-14沈敏
沈敏

【摘要】 教学技能是数学教师教学能力的重要组成部分,随着“翻转课堂”的出现,教师的教学技能相比于传统教学又有了新的内涵,因此,探讨“翻转课堂”理念下教师的数学教学技能显得尤为重要. 本文通过具体的数学情境阐述“翻转课堂”理念下教师应具备的数学教学技能:筛选、整合数学信息的技能、自学并制作数学视频的技能以及正确使用数学专业软件的技能.
【关键词】 翻转课堂;教师;数学;教学技能
教学技能是数学教师教学能力的重要组成部分,传统课堂数学教学技能包括导入、板书、演示、讲解、提问、反馈和强化、结束、组织教学、变化等,而在“翻转课堂”模式下,传统的数学教学技能远不能满足新的需求,数学教师还需要具备交流合作与沟通等新的教学技能. 因此,探讨“翻转课堂”理念下教师应具备的数学教学技能是非常有必要的.
在参考已有研究成果,并对“翻转课堂”理念下教师应具备的数学教学技能进行深入研究的基础上,本文将从以下三个方面具体阐述“翻转课堂”理念下教师应具备的数学教学技能:
(一)筛选、整合数学信息的技能
在“翻转课堂”模式下,教师视频的录制品质、教师的讲解等资源对学生具有很强的引领性和启发性. 因此,数学教师在录制的视频时,需要具备筛选、整合数学信息的技能,这样才能激发学生的数学学习兴趣和参与热情,从而进一步引导他们解决问题. 以高中数学人教版教材中《函数的单调性》为例,在这一节,学生需要建立对增(减)函数的概念、掌握用定义证明函数单调性的基本方法与步骤. 因此,教师在录制视频时,不妨先从简单的一次函数y = x入手,引导学生观察其图像的变化特点;再选取与之不同的二次函数y = x2,通过对比,发现它们在图像升降上的不同特点;然后以y = x2在y轴右边的图像为例引导学生用数学符号语言来描述这种“上升”的变化;最后,在引出增函数定义后,引导学生通过类比定义减函数的数学符号语言. 在视频的结尾,教师可以选取反比例函数y = ,启发学生思考此函数是否为减函数.
在整个视频的制作过程中,教师筛选、整合不同类型函数的能力,不仅可以有效控制视频录制的时间长短,而且更有利于学生观察发现.
(二)自学并制作数学视频的技能
在传统课堂中,数学教师通过写板书、放投影仪等促进学生的学习. 而在翻转课堂模式下,学生需通过观看教师课前录制的视频学习新知. 调查发现,很大一部分数学教师不懂如何拍摄视频、录制、剪辑等技术,也不会使用录制视频软件来制作课件,这为翻转课堂带来了一些瓶颈. 因此,数学教师需利用空闲时间自学使用软件(如:汗微·微课宝)制作视频,对于老教师而言,则可以选择计算机录屏技术,它不仅能够把教师操作计算机的过程记录下来形成视频,而且对录屏技术的要求较低,易学会、易普及. 从这一角度,翻转课堂对数学教师自学并制作视频的能力提出了一定要求.
在学会录制视频后,数学教师录制的视频内容是影响学生学习并掌握新知的关键. 以小学数学人教版教材中的《画垂线》为例,学生之前已经学习过垂线的定义,本节课要学习如何画垂线,教师可录制如下教学视频:
师:你能画出互相垂直的两条直线吗?
(给学生留两分钟思考时间)
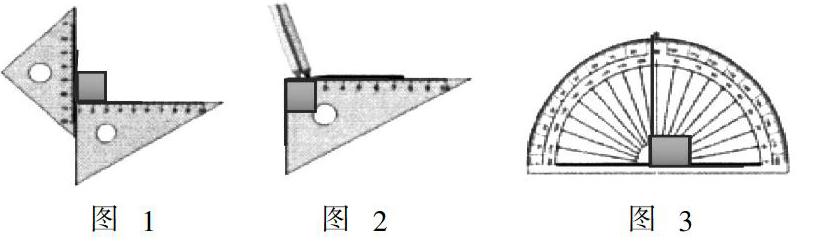
师:大家都已有了答案,老师在这里展示三种画垂线的方法,第一种是利用两把三角尺来画(如图1,教师用实物亲自展示),将一把三角尺的边与另一把直角三角尺的一条直角边重合,再沿着两把三角尺的边画两条直线,并标上直角符号(如图2,教师用实物亲自展示);第二种是直接利用一把直角三角尺来画,沿着两条直角边画两条垂线,并标上直角符号;第三种是用量角器先画出一条直线并在直线上任意标一个点,将量角器的零刻度线与所画直线重合,然后将量角器的中心点与所标出的点重合,在量角器的90度处标上一点,最后将两点连接起来并标上直角符号(如图3教师用实物展示).
师:大家都学会了吗?
师:接下来请大家想想:怎样过直线上一点画已知直线的垂线呢?
(给学生留两分钟思考时间)
师:在这里,老师给你们展示两种画法.
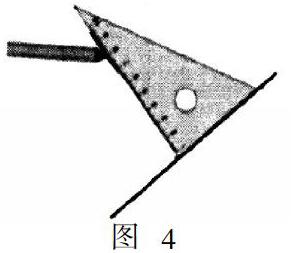
第一种:①把三角尺的一条直角边与已知直线重合;②移动三角尺使三角尺的顶点与这个点重合;③沿着另一条直角边画一条直线,这条直线就是已知直线的垂线,最后标出直角符号(如图4所示,教师用实物亲自展示)
第二种:①把三角尺的一条直角边与已知直线重合;②沿着直线移动三角尺,使三角尺的另一条直角边与这个点重合;③再沿着三角尺画一条直线,这条直线就是已知直线的垂线,最后标出直角符号(教师用实物亲自展示)
师:我们现在已经学会如何过直线上一点画已知直线的垂线了,那么如果这个点不在直线上,你还能画出已知直线的垂线吗?
(给学生留两分钟思考时间)
师:其实,在过直线外一点画已知直线的垂线与过直线上一点画已知直线的垂线的画法是一样的,下面老师给大家展示一下老师的画法,你们看看自己是不是和老师想得一样呢?
师:①把三角尺的一条直角边与己知直线重合;②沿着直线移动三角尺,使三角尺的另一条直角边经过这个点;③再沿着这条直角边画一条直线,这条直线就是已知直线的垂线,最后标出直角符号(如图5,教师用实物亲自展示)
师:这节课我们学习了如何过直线上一点或直线外一点画已知直线的垂线,下面请大家看一看以下两种画垂线的方法对吗?(如图6,图7,教师用实物动态展示两种画垂线的错误方法)如果这两种画法不对,那分别错在哪呢?请大家课后思考一下.
(三)正确使用数学专业软件的技能
高度抽象的学科特点,决定了数学从对象到思想方法上都是抽象的. 特别是在翻转课堂这样的教学模式下,教师无法直接观测学生的表情与注意力,如果一昧地讲解抽象的知识点,学生很难理解,甚至容易分心. 而一些数学专业软件的出现,则会引起学生的高度注意,并且可以直观有效地帮助学生理解新知. 因此,在翻转课堂模式下,数学教师在录制视频的同时,需要具备正确使用一些数学专业软件(如:几何画板、MATLAB)的技能. 比如:在录制初中数学苏教版教材中的《三角形的中位线》的视频时,教师在引入中位线定义后,引导学生通过测量中位线与三角形第三条边的长度来猜测三角形中位线与第三条边的长度关系. 在这个过程中,教师可以利用几何画板,在画板上任意选取三个不同的点作为一个三角形的三个顶角,并根据坐标可以准确表示画出其中位线,再通过几何画板的长度度量,很容易得出中位线与三角形第三条边的长度关系. 同时,学生可以根据得到的图形判断其位置关系,这样不仅省去了由于测量上的误差带来的错误结论,也更有利于学生直观的学习.
【参考文献】
[1]张波,季素月.课改背景下师范生教学技能的内涵探究及培训模式建构[J].扬州大学学报,2010,14(3).
[2]陈明选,陈舒.围绕理解的翻转课堂设计及其实施[J].高等教育研究,2014,(12).
[3]徐汉文.《中学数学课程标准与教材分析》[M].科学出版社,2014.
[4]付小倩,袁顶国.中国式“翻转课堂”的实践困境与突围[J].现代中小学教育.2014,(7):45-48.
[5]陈凤燕.“翻转课堂”:信息技术与教育的深度融合[J].教育评论,2014,(6).
[6]高楠.翻转课堂在小学数学教学中的应用研究—以“画垂线为例”[D].天津:天津师范大学,2015
[7]柳成行.数学教师现代信息技术能力的自我培养[J].成人教育.2010,(11).
