基于小波消噪和希尔伯特黄变换的损伤检测技术研究*

聂杰文， 徐明强， 王树青

(山东省海洋工程重点实验室，中国海洋大学，山东 青岛 266100)



基于小波消噪和希尔伯特黄变换的损伤检测技术研究*

聂杰文， 徐明强， 王树青**

(山东省海洋工程重点实验室，中国海洋大学，山东 青岛 266100)

摘要：针对经验模式分解(EMD)易受噪声影响的缺点，提出采用小波消噪结合Hilbert-Huang变换的结构损伤检测方法。首先对含噪声振动信号进行小波消噪预处理实现信噪分离，再进行EMD分解得到若干固有模态函数(IMF)，利用希尔伯特(Hilbert)变换得到其瞬时频率。提出了一个基于低阶瞬时频率变化率的损伤判定指标，利用此指标可以判断损伤是否发生。数值研究结果表明小波消噪结合HHT的方法是进行损伤检测比较有效的方法。

关键词：小波变换； 经验模式分解； Hilbert变换； 损伤检测； 瞬时频率

引用格式：聂杰文，徐明强，王树青. 基于小波消噪和希尔伯特黄变换的损伤检测技术研究[J]. 中国海洋大学学报(自然科学版)， 2016, 46(4)： 142-148.

NIE Jie-Wen, XU Ming-Qiang, WANG Shu-Qing . Research on structural damage detection based on wavelet de-noising and hilbert-huang transform[J]. Periodical of Ocean University of China, 2016, 46(4): 142-148.

结构的损伤检测是结构健康监测的重要内容。结构物的健康状况一般是由实测的振动信号进行分析、诊断和评估。由于结构或设备的工作环境复杂，噪声干扰比较多，经常使得有用的损伤特征信号淹没在较强的背景噪声中，难以准确地进行损伤检测。如何从结构振动信号中去除噪声，并提取出损伤特征信号是非常具有研究价值的。Norden E.Huang等人[1]于1998年提出了一种新的非平稳信号的时频分析方法—希尔伯特黄变换法(HHT)；1999年，Huang[2]又将该方法进行了一些改进。希尔伯特黄变换由经验模式分解(EMD)和Hilbert变换两部分组成，其中EMD方法是基于信号的局部时间尺度进行分解，相对于其他信号处理方法的最大优势在于自适应性，特别适合处理非线性非平稳信号，因此这一技术已经在损伤检测领域得到广泛应用[3-6]。但是EMD方法受噪声干扰影响较大，分解精度会因噪声的影响而降低。而小波变换是目前应用非常多，效果较好的降噪方法[7-9]。本文研究首先采用小波变换对含噪声信号进行处理，然后进行EMD分解得到若干固有模态函数(IMF)，选取感兴趣的IMF进行Hilbert变换得到其瞬时频率，最后提出了基于瞬时频率变化的损伤指标用于判断损伤。利用该方法对一个三层剪切模型的振动信号进行处理，验证了该方法在损伤检测中的可行性。

1信号的小波降噪处理

在实际应用中，一般采用离散小波变换对信号进行处理，对于任意平方可积函数f(t)来说，其离散小波变换(DWT)为：

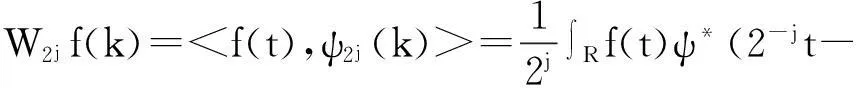
(1)

1987年，Mallat利用多分辨分析的思想，统一了小波函数的构造，提出了离散信号小波变换的分解和重构算法。对任意f(x)∈Vj，若fk为信号的离散采样数据，令cj,k=fk，则信号的多分辨率分析公式为：

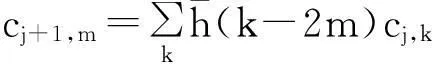
(2)

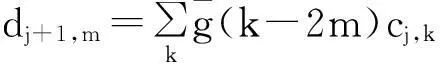
(3)

其中：cj,k为信号的逼近信号；dj,k为信号的细节。则信号的重构公式为：

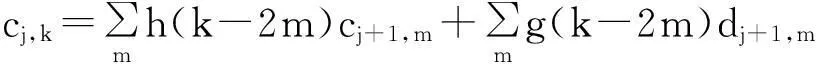
(4)

信号的小波分解过程，可看成是分别对信号作用低通滤波器得到近似信号以及作用高通滤波器得到细节信号的过程。实际采集到的信号中，噪声信号多包含在高频的细节信号中，这样，对小波分解后的高频细节系数进行门限阈值处理，然后再进行小波重构，就可以达到消噪的目的。

用小波阈值方法对信号进行降噪的过程可分为3个步骤[10]：

(1)振动信号的小波分解。选择一个合适的小波基并确定分解层次，然后进行分解计算。

(2)小波分解后高频系数的阈值量化。对各分解尺度下的高频系数选择一个阈值进行量化处理。

(3)一维小波重构。根据小波分解的最底层低频系数和各层的高频系数进行一维小波重构。

2希尔伯特-黄变换(HHT)

HHT是NASA的Huang N E等人[1]于1998年提出的，主要包括两大步骤：首先是应用经验模式分解(EMD)，将信号分解成一系列固有模态函数(Intrinsic Mode Function，简称IMF)；其次对每一个IMF进行Hilbert变换，得到固有模态函数的瞬时相位(频率)和振幅，最终将所有结果表示成振幅-频率-时间的分布图，即Hilbert谱。

2.1 经验模式分解

EMD分解的目的是根据信号的局部时间尺度，按频率由高到低把信号分解成有限个固有模态函数(IMF)的和，其中各个IMF都必须是窄带信号，以便进行Hilbert变换。EMD分解所得的IMF必须满足2个条件：(1)在整个数据序列中，极值(包括极大值和极小值)的个数和过零点的个数必须相等或至多相差一个；(2)由任意局部极值点所确定的上下包络线的均值必须是零。

EMD分解的具体步骤如下：

(1)确定信号s(t)的所有极大值点和极小值点，用三次样条曲线分别连接局部极大值点和极小值点拟合成s(t)的上包络线和下包络线，计算上下包络线的均值m1(t)。将原数据序列s(t)减去该平均包络m1(t)，求出：

s(t)-m1(t)=h1(t)。

(5)

如果h1(t)是一个固有模态分量，那么h1(t)就是s(t)的第一个分量。

(2)通常，h1(t)不满足固有模态函数的条件，因此把h1(t)作为初始数据，重复式(5)k次，得到h1k(t)=h1(k-1)(t)-m1k(t)，使得h1k(t)变为一个IMF。令c1(t)=h1k(t)，则c1(t)为信号s(t)的第一个IMF分量。

(3)c1(t)代表了原始数据序列中最高频的组分，将原始数据序列s(t)减去第一个IMF分量c1(t)，得到：

r1(t)=s(t)-c1(t)。

(6)

将r1(t)作为原始数据重复步骤(1)和(2)，得到s(t)的第二个满足固有模态函数条件的分量c2(t)，重复循环n次，直到rn(t)变成单调函数并且不能再提取出IMF时，筛选过程就可以停止。

通过EMD方法，信号s(t)可以自适应地分解为多个在任意时刻只有单一振动频率的固有模态函数和一个剩余分量，如下式所示：

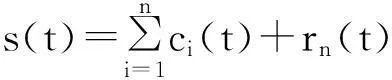
(7)

式中：ci(t)为分解所得的第i个IMF；rn(t)是经分解所得的残余函数，常常代表信号的直流分量或平均趋势。

2.2 希尔伯特谱

对时间序列x(t)的Hilbert变换y(t)可表示为：

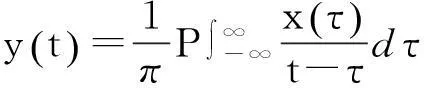
(8)

其中P表示柯西主值。因此，就可以用x(t)和y(t)来定义一个解析信号z(t)，如下所示：

z(t)=x(t)+iy(t)=a(t)eiθ(t)，

(9)

其中：

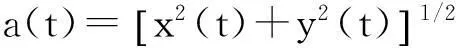
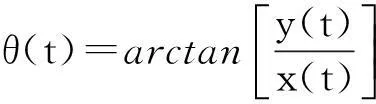
(10)

则由公式(10)可得瞬时频率表示如下：

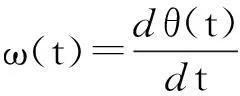
(11)

从式(11)中可以看出，瞬时频率是时间的单值函数，而在文献[1]中作者对固有模态函数提出的限制条件使得瞬时频率有了真实的物理意义，而不仅仅是个数学定义。对式(7)中的每个IMF分别作Hilbert变换后，可将原始信号表示成：

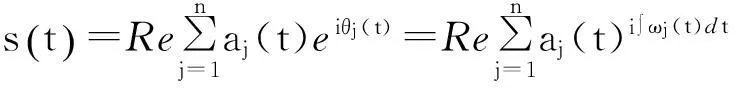
(12)

上式中省略了残余函数rn(t)，Re表示取实部。公式(12)还可以表示成如下形式：

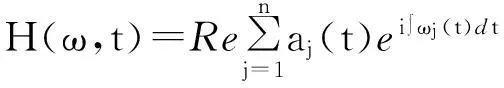
(13)

根据公式(13)，可以在一个三维坐标系中把振幅表示成瞬时频率和时间的函数。把振幅的这种时频分布称为Hilbert幅值谱，简称Hilbert谱。由于Hilbert谱中的频率是由局部时间尺度定义的，因此它具有很高的频率分辨率，能更好地应用于分析信号的频率变化。

HHT方法从本质上讲就是把一个复杂的信号进行平稳化处理，将信号中不同时间尺度的波动逐级分解出来，产生一系列具有不同特征尺度的固有模态函数。对这些固有模态函数进行Hilbert变换就可以得到信号的时频谱(Hilbert谱)图，Hilbert谱反映的就是系统原有的特性。

3仿真信号研究

本节首先通过对一个仿真信号进行分析验证基于小波消噪的EMD分解过程的优越性。考虑一个由白噪声信号和三谐波信号叠加而成的含噪信号，其表达式如下：

s(t)=sin(4πt)+3sin(10πt)+4sin(20πt)。

(14)

其中3个谐波的频率分别为2、5、10Hz，幅值分别为1、3、4。为了研究噪声对EMD分解的影响，在信号s(t)上添加高斯白噪声，噪声的添加方式如公式(11)所示[11]。

s*(t)=s(t)(1+nγ)。

(15)

其中：s*(t)为含噪声信号；n代表噪声水平(本例中n=15%)；γ为均值为0、方差为1的高斯白噪声。经EMD分解后得到的各IMF分量及前四阶IMF的PSD如图1所示。从图1b前四阶IMF的频谱图可以看出，第二阶IMF频谱中有2个较明显的峰值，分别对应着5和10Hz，说明第二阶IMF中含有2种谐波成分，第三阶IMF的频谱中含有3个比较明显的峰值，说明存在3种主要频率成分，这表明噪声的存在使得EMD分解结果出现了模态混叠现象，在同一个IMF中出现了不同时间尺度的频率成分(或者同一时间尺度的频率成分出现在不同的IMF中)。另外，前四阶IMF的PSD中还含有许多小的峰值，可见EMD分解精度受噪声干扰的影响较大，噪声的存在使得EMD分解产生了许多虚假模态。因此，对于有噪声影响的信号，进行EMD分解之前应该先进行消噪处理。

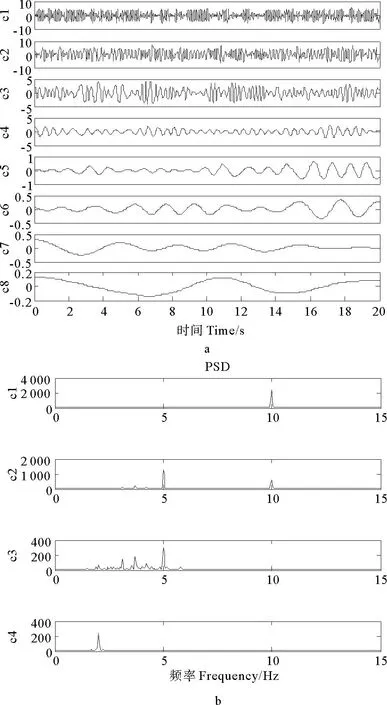
图1　含噪声信号EMD分解结果及前四阶IMFs频谱

图2是经过Daubechies小波中的db45小波消噪之后的分解结果。对比图1和2可以得出，小波消噪之后，分解得到的IMF数量明显减少，同时也消除了模态混叠现象。图2b中显示的前3阶IMF频率分别对应3个谐波的频率。图3是无噪声信号直接进行EMD分解的结果。对比图2和3可以发现，小波消噪之后再

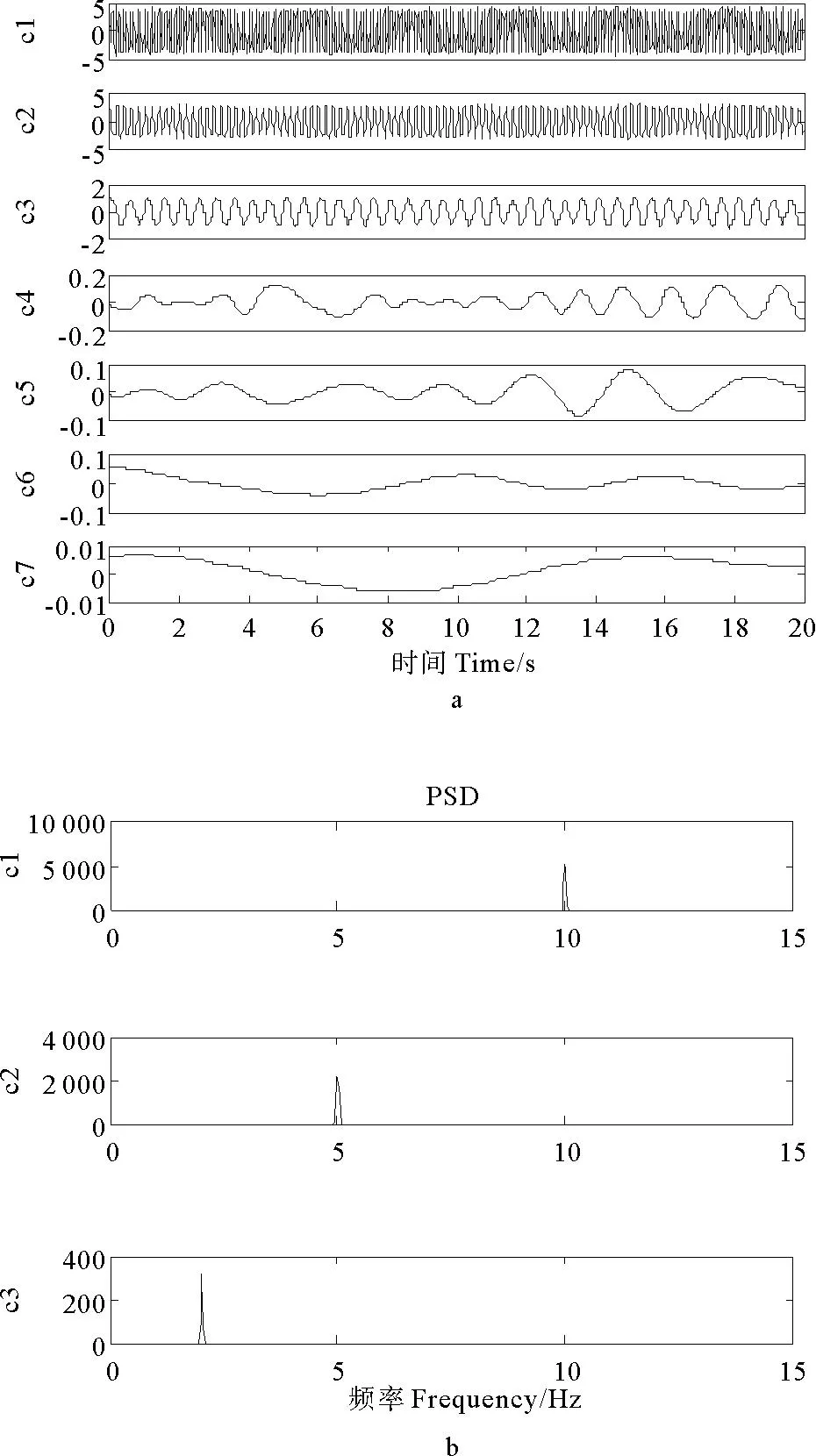
图2　小波消噪信号EMD分解及前三阶IMFs频谱

图3　无噪声信号EMD分解结果及前三阶IMFs频谱

进行EMD分解和无噪声信号直接进行EMD分解得到的结果相差不大，进一步表明了小波消噪较好地消除了噪声的影响。模拟实验说明先进行小波消噪再做EMD分解，会大大提高EMD分解的精度。

4三层剪切模型损伤检测

通过以上的分析可知，为提高EMD分解的精度，在进行EMD分解之前应该首先对信号进行消噪处理。本文采用一个典型的三层剪切模型进行研究，系统模型如图4所示。模型的质量和刚度分别为：M1=1kg，M2=1.5kg，M3=2kg，K1=600N/m，K2=1200N/m，K3=1800N/m。进行模态分析可以得到模型的三阶固有频率依次为2.3112、4.9414和7.3370Hz。

4.1 EMD分解分析

采用刚度的减小来模拟损伤，在第10s时，假设K2突然减小20%。损伤后，模型各阶固有频率依次为2.2079、4.9398和6.8718Hz。在M3上施加一个振幅为10N、频率为1Hz的稳态简谐荷载，持续时间20s。采用Newmark法进行振动响应计算，采样频率为100Hz。图5所示分别为M1、M2和M3的加速度响应信号以及它们的PSD。从图中可以看出M1的加速度响应信号中最高阶的频率成分几乎没有，而M2和M3的响应信号中都包含有三阶频率成分，因此在下边的分析中都采用M2的加速度响应信号。

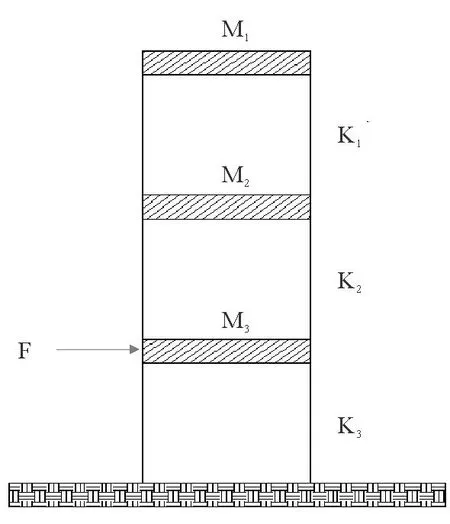
图4　三层剪切模型

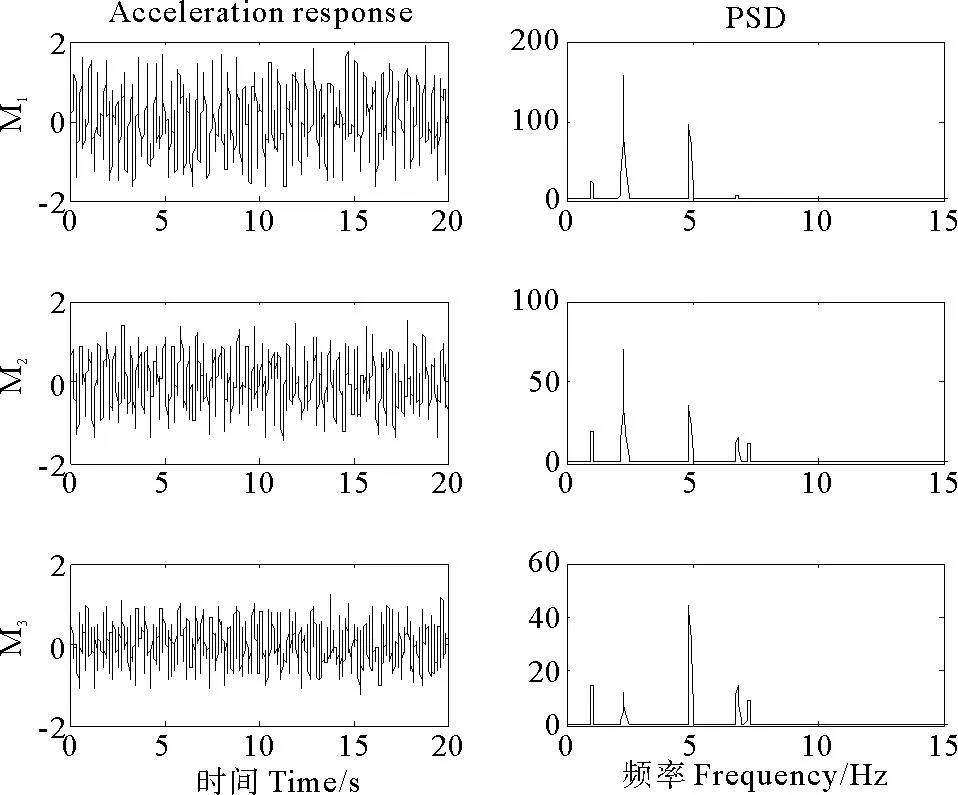
图5　加速度响应信号及其PSD

用式(11)所示的方法在M2的加速度响应信号中添加10%的白噪声进行分析，首先采用Daubechies小波中的db45小波进行消噪，再进行EMD分解。所得EMD分解结果及前四阶IMF的频谱图如图6所示。从图6b可以看出，第一阶IMF的PSD中有两个峰值，表明包含2种频率成分的信号，说明模型的最高阶固有频率发生了变化。第四阶IMF频率为1Hz，对应外部激励力的频率。第二和第三阶IMF的PSD中分别只有一个峰值，没能反映出结构本身的固有频率变化。而模态分析结果表明第一阶固有频率在损伤前后改变了6.3%，第二和第三阶固有频率在损伤前后分别改变了0.03%和4.4%，所以仅依靠观察EMD分解之后得到的IMFs及其PSD无法有效地检测损伤的发生。在下边的分析中，拟采用一个合适的指标来表征损伤，通过检测这个指标的变化就能够比较精确地进行损伤检测。

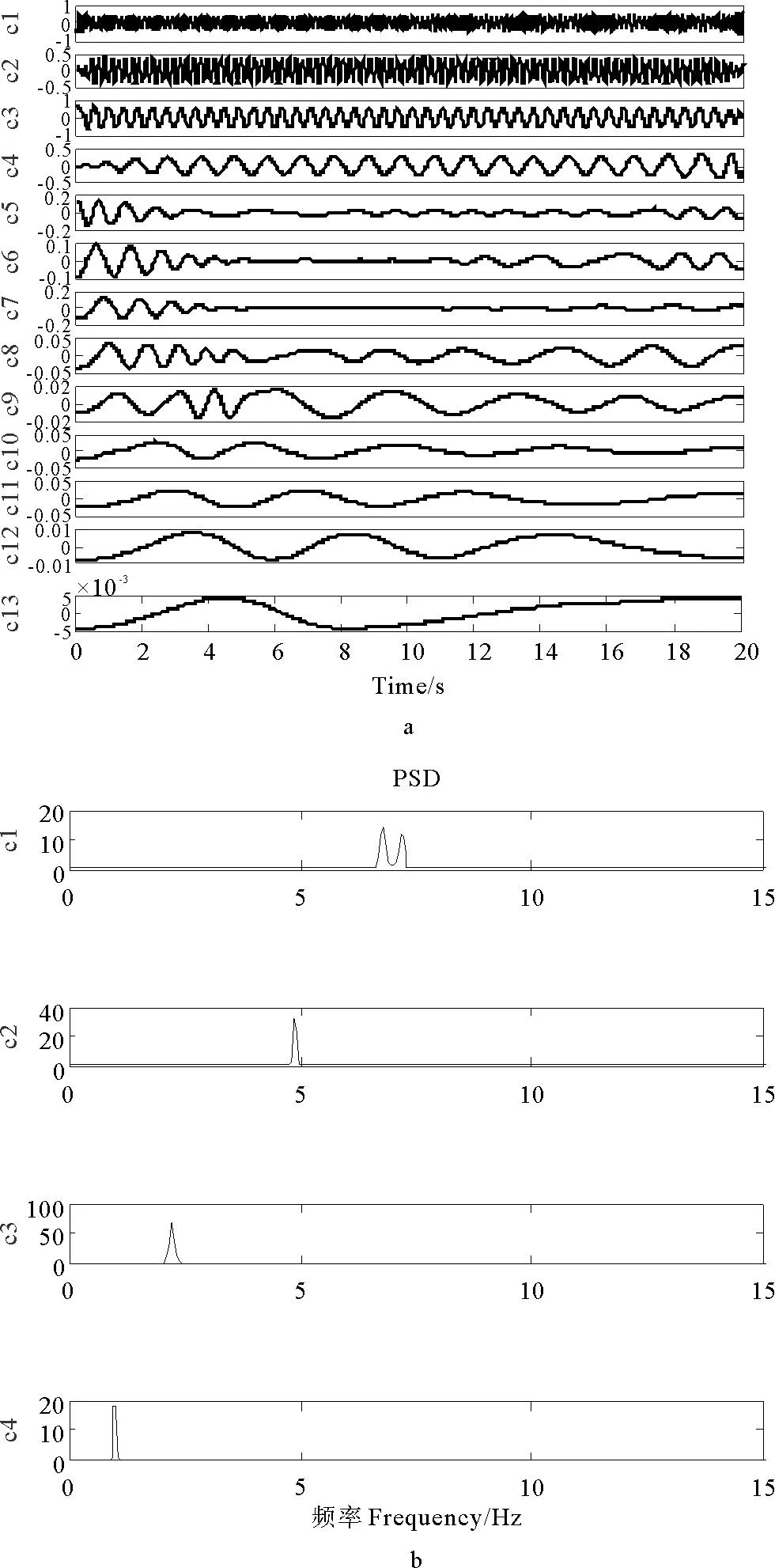
图6　小波消噪信号EMD分解及前四阶IMFs的频谱

4.2 瞬时频率分析

由于EMD是根据信号的局部时间尺度进行分解，所以得到的IMF具有很高的频率分辨率。对图6得到的前三阶IMF进行分析，可以得到瞬时频率随时间的变化曲线，如图7所示。可以看出第1和3阶IMF的频率在10s附近发生了变化。对瞬时频率进行分段直线拟合，结果如图7中的直线所示。由图7可见，红线拟合出的频率正好对应模型损伤前的三阶固有频率，而蓝线拟合出的频率对应的是模型损伤之后的频率。其中，IMF1和IMF3的瞬时频率拟合曲线在第10s时都出现了明显的突变，说明结构在第10s时发生损伤。而且IMF1的变化幅度要大于IMF3的变化幅度，与理论计算数据是一致的，这也进一步证明了EMD分解具有较高的频率分辨率。而IMF2的瞬时频率拟合曲线在第10s时没有明显变化，这是因为第二阶频率在损伤前后变化很小，所以在拟合图中没有出现明显的突变，这与理论计算结果也是相同的。

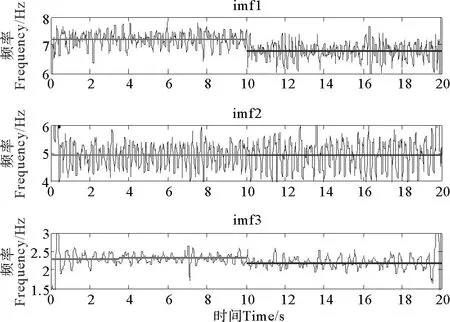
图7　瞬时频率拟合曲线图

从以上分析可以发现，瞬时频率对损伤的出现比较敏感。为了更有效地对结构的损伤进行监测，研究以瞬时频率为基础，提出基于瞬时频率变化率(Frequency Change Rate-FCR)的损伤检测指标σ，其定义如式(16)所示，

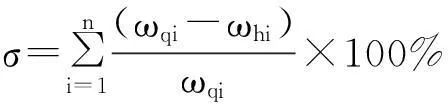
(16)

其中：ωqi和ωhi(i=1,…,n)分别代表损伤前和损伤后的瞬时频率；n为识别的瞬时频率的阶数，本文中n=3。为了给σ确定一个合适的阈值，以便用于损伤预警，研究了不同损伤程度(这里损伤程度指的都是K2刚度损失的大小，包括2%、3%、5%、8%、10%、20%和30%七种情况)、不同噪声背景(包括无噪声以及含1%、5%、10%、20%和30%的噪声6种情况)下的损伤检测，结果如表1所示。其中，前三阶频率变化率之和指的是K2刚度发生损失时，前三阶频率变化率之和的理论值。

由表1可以看出，在无噪声影响时，后6种损伤工况下检测得到的σ值与理论频率变化率都非常接近，说明在这6种情况下都可以检测到损伤的发生，同时也表明EMD分解具有较高的频率分辨率。在有噪声影响的情况下，损伤程度一定时随着噪声水平的逐渐增加，检测得到的σ值逐渐减小，说明噪声会对损伤检测的结果造成影响。后6种损伤工况下，添加的噪声水平在1%～10%之间时，检测得到的σ值与无噪声情况下检测得到的σ值都相差不大，都能检测到损伤的发生；添加的噪声水平为20%时，只有损伤程度为3%和5%两种工况下检测得到的σ值与无噪声情况下检测得到的σ值相差较大，但是仍然能够检测到损伤的发生；这说明小波消噪结合HHT是一种比较有效的损伤检测方法。当损伤程度为2%时，即使添加的噪声水平很小，也无法有效检测到损伤的发生，这表明损伤程度的大小对损伤检测的结果影响很大。而当添加的噪声水平达到30%，损伤程度达到30%时才能有效检测到损伤，而损伤程度为3%至20%五种损伤工况下检测得到的σ值都远远偏离理论频率变化率，不能有效检测到损伤的发生。这表明当背景噪声非常强时，损伤特征信息会淹没在强大的噪声中，导致无法有效地检测损伤。

表1　不同损伤工况下的检测结果

5结语

针对EMD分解精度容易受噪声干扰这一缺点，首先利用小波变换对信号进行消噪处理，然后再进行EMD分解。将这种方法应用于三层剪切模型的损伤检测，为了有效地对结构状况进行监测，提出了基于瞬时频率变化的损伤检测指标，并用此指标进行了不同工况下的分析研究，研究结果表明，本文提出的损伤检测指标具有较好的鲁棒性，在噪声小于20%时可以得到较好的检测结果，基于小波消噪的HHT方法是一种比较有效的损伤检测方法。在实际应用中，结构损伤的发生在时间上具有不确定性，因此可以采用对采样数据分成许多尽量短的时间段进行分析对比，确定损伤发生的时间。此外小波消噪并不能完全消除噪声的影响，如何能更加有效的消除噪声,并应用于实际状态下复杂结构的损伤检测将是今后的研究方向。

参考文献：

[1]Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London Series, 1998, A454: 903-995.

[2]Huang N E, Shen Z, Long S R. A new view of nonlinear water waves: the Hilbert spectrum[J]. Annual Review of Fluid Mechanics, 1999, 31: 417-457.

[3]Anshuman Kunwar, Ratneshwar Jha, Damage detection in an experimental bridge model using Hilbert-Huang transform of transient vibrations[J]. Struct Control Health Monit， 2013， 20: 1-15.

[4]Dejie Yu, Junsheng Cheng, Yu Yang. Application of EMD method and Hilbert spectrum to the fault diagnosis of roller bearings[J]. Mechanical Systems and Signal Processing 2005，19： 259-270.

[5]陈忠, 郑时雄. 基于经验模式分解(EMD)的齿轮箱齿轮故障诊断技术研究[J]. 振动工程学报, 2003, 16(2): 229-232.

Chen Zhong, Zheng Shixiong, Study on fault diagnosis of gears using Empirical Mode Decomposition[J]. Journal of Vibration Engineering, 2003, 16(2): 229-232.

[6]Bernal, Dionisio, Burcu Gunes. An examination of instantaneous frequency as a damage detection tool[C]. Proc 14th Engineering Mechanics Austin: Conf, TX, 2000.

[7]徐仁林, 安伟. 小波降噪在信号基于EMD的Hilbert变换中的应用[J]. 噪声与振动控制, 2008(3): 74-77.

Xu Renlin, An Wei, Wavelet denoise application in the signal hilber transform based on EMD[J]. Noise and Vibration Control, 2008(3): 74-77.

[8]罗忠辉, 薛晓宁, 王筱珍，等. 小波变换及经验模式分解方法在电机轴承早期故障诊断中的应用[J]. 中国电机工程学报, 2005, 25(14): 125-129.

Luo Zhonghui, Xue Xiaoning, Wang Xiaozhen. Study on the method of incipient motor bearing fault diagnosis based on wavelet ransform and EMD[J]. Proceedings of CSEE, 2005, 25(14): 125-129.

[9]王龙, 沈艳霞, 季凌燕. 基于小波降噪和EMD方法的风力发电系统齿轮箱故障诊断[J]. 江南大学学报, 2012, 11(2): 159-162.

Wang Long, Shen Yanxia, Ji Lingyan, Wind turbine gearbox fault diagnosis based on wavelet de-noising and EMD[J]. Journal of Jiangnan University[J], 2012, 11(2): 159-162.

[10]Donoho L D. De-noising by soft-thresholding[J]. IEEE Trans Inf Th, 1995, 41(3): 613-627.

[11]Shuqing Wang. Damaged detection in offshore platform structures from limited modal data[J]. Applied Ocean Research, 2013,41: 48-56.

[12]侯立群, 欧进萍. 环境激励及噪声干扰下斜拉桥的损伤定位方法[J]. 振动与冲击, 2008, 27(8): 1-6.

Hou Liqun, Ou Jinping. Damage localization method of long-span cable-stayed bridges under ambient excitation and noise disturbance, Journal of Vibration and Shock, 2008, 27(8): 1-6.

责任编辑陈呈超

研究简报

Research on Structural Damage Detection Based on Wavelet De-Noising and Hilbert-Huang Transform

NIE Jie-Wen, XU Ming-Qiang, WANG Shu-Qing

(Shandong Provincial Key Lab of Ocean Engineering, Ocean University of China, Qingdao 266100, China)

Abstract：In view of the shortcoming of the empirical mode decomposition (EMD)whose precision is subject to noise effect, Hilbert-Huang transformation combined with the wavelet de-noising for structural damage detection is proposed. First, the theoretical background of the wavelet-based de-noising method and the Hilbert-Huang transform is presented. In the first step, the noisy vibration signal is pre-processed with wavelet transform to separate the signal from noise. In step two, Empirical Mode Decomposition (EMD) is carried out to obtain the Intrinsic Mode Functions (IMFs). In the third and final stage, Hilbert transform is applied to the interested IMFs to get the instantaneous frequencies. A new damage indicator based on the instantaneous frequencies is proposed to determine whether the damage had occurred. The damage detection index, defined as the sum of the first three frequency change rate (FCR), can be used for damage detection. The wavelet based de-noising and Hilbert-Huang transform are firstly verified by using a simulated signal with three dominant frequencies. Then a three-story shear building model is used for the damage detection. Numerical results of the study showed that the proposed method is effective for structural damage detection.

Key words：wavelet transform; EMD; Hilbert transform; damage detection； instantaneous frequency

DOI：10.16441/j.cnki.hdxb.20140144

中图法分类号：TU317

文献标志码：A

文章编号：1672-5174(2016)04-142-07

作者简介：聂杰文(1988-)，男，硕士生。**通讯作者： E-mail:shuqing@ouc.edu.cn

收稿日期：2014-06-18；

修订日期：2015-06-20

*基金项目：国家自然科学基金项目(51379196)；泰山学者工程专项经费资助

Supported by the National Natural Science Foundation of China(51379196) and the Taishan Scholars Program of Shandong Province