基于峰度和小波变换的超短波信号调制识别

谢跃辉++张一闻++赵亚欣++宋德鹏

摘 要： 针对FM，MSK，QPSK三种具体调制方式，由于在高斯白噪声环境中小波变换幅度方差区分MSK，QPSK调制信号效果较差，以及在不同信噪比条件下零中心归一化瞬时幅度谱密度的最大值对FM，MSK和QPSK识别效果的下降，提出利用峰度和基于小波变换特征量的方法对信号分类识别。该方法首先利用峰度进行模拟与数字调制信号的类间识别，然后采用基于小波变换系数提取的特征量对两种数字调制信号进行识别分类。采用决策树分类方法，利用Matlab对该方法进行仿真验证，仿真结果表明该方法具有较好的识别效果。

关键词： 调制识别； 超短波信号； 峰度； 小波变换； 高斯白噪声

中图分类号： TN911.7?34 文献标识码： A 文章编号： 1004?373X（2016）23?0009?04

Ultrashort wave signal modulation recognition based on wavelet transform and kurtosis

XIE Yuehui， ZHANG Yiwen， ZHAO Yaxin， SONG Depeng

（Department of Information Engineering， Engineering College of CAPF， Xian 710086， China）

Abstract： Aiming at three specific modulation modes of FM， MSK and QPSK， the effect of differentiating MSK and QPSK modulation signals with wavelet transform amplitude variance is poor in white Gaussian noise （WGN） environment， and the maximum instantaneous amplitude of zero center normalized spectral density has bad effect to recognize the FM， MSK and QPSK mo?dulation signals under the conditions of different signal?to?noise ratios， so the characteristic quantity method based on kurtosis and wavelet transform used for signal classification and recognition is put forward， in which the kurtosis is used for type identification of analog modulation signal and digital modulation signal， and then the characteristic quantity extracted on the basis of wavelet transform coefficient is used to recognize and classify the two digital modulation signals. The decision tree classification method is adopted to carry out simulation verification of the method by means of Matlab. The simulation results show this method has better recognition effect.

Keywords： modulation recognition； ultrashort wave signal； kurtosis； wavelet transform； WGN

0 引 言

在无线通信领域中，软件无线电的应用越来越广。通信信号的调制方式识别是软件无线电的核心技术之一，它是非合作通信信号处理研究领域的一个十分重要的课题，其目的就是在未知调制信息的前提下，从接收信号中分析出通信信号的调制方式，并估计出相应的调制参数，为后续的信号处理做准备。FM模拟调频是目前采用最多的超短波通信调制方式；MSK调制信号作为一种连续相位调制方式，具有抗非线性失真能力强、频带利用率高和设备实现简单的特点，是一种重要的超短波调制方式；QPSK调制信号的频谱利用率高和抗干扰性强的特点，使其成为超短波的一种常用调制方式。在下一步的超短波电台设计中将采用这三种调制方式。文献[1]指出目前调制方式自动识别的研究方法主要可以分为两类：一是基于假设检验的最大似然方法；二是基于特征提取的模式识别方法。基于假设检验的最大似然方法是通过对信号的似然函数进行处理，将得到的似然比与阈值进行比较，完成调制识别功能；基于特征提取的模式识别方法，通常包含两个子系统，一个子系统用于提取信号的特征参数，另一个子系统根据信号的特征参数，采用一定的分类器确定信号的调制类型。从贝叶斯估计的意义上来说，基于最大似然方法的分类结果是最优的，但是其表达式通常比较复杂，计算复杂度较高，不利于在线分析，而且这类方法对模型失配和参数偏差问题比较敏感，稳健性较差。基于特征提取的模式识别方法，在理论上是一种次优的方法，但是其形式通常比较简单，易于实现，而且在某些条件下能够达到近似最优的识别性能，在模型失配的情况下，其稳健性也强于最大似然法。

文献[2]表明可以先利用非弱信号段上零中心、归一化瞬时频率的一阶绝对原点矩将QPSK调制信号同FM和MSK调制信号分开，再利用归一化瞬时频率峰度将FM调制信号与MSK调制信号分开。但由于其特征参数均是在理想无噪声的情况下提取得到，故应用范围不高。

在对MSK和QPSK调制信号识别分类方面，文献[3]分析表明，可以利用高阶累积量[C40]完成识别分类，但是其高阶累积量的理论值均在符号等概率付出、零噪声、平均功率归一化的条件下得到，实际应用范围受到限制。文献[4]提出观察信号循环谱密度[Sαxf]在[f=0]的截面（[Sαx0]）有无明显谱峰，利用特征参数[maxSαx0DsubmaxSαx0]完成识别分类，平均识别率在信噪比高于8 dB时大于80%，但是其对信噪比要求较高且计算相对复杂。

1 研究方法概述

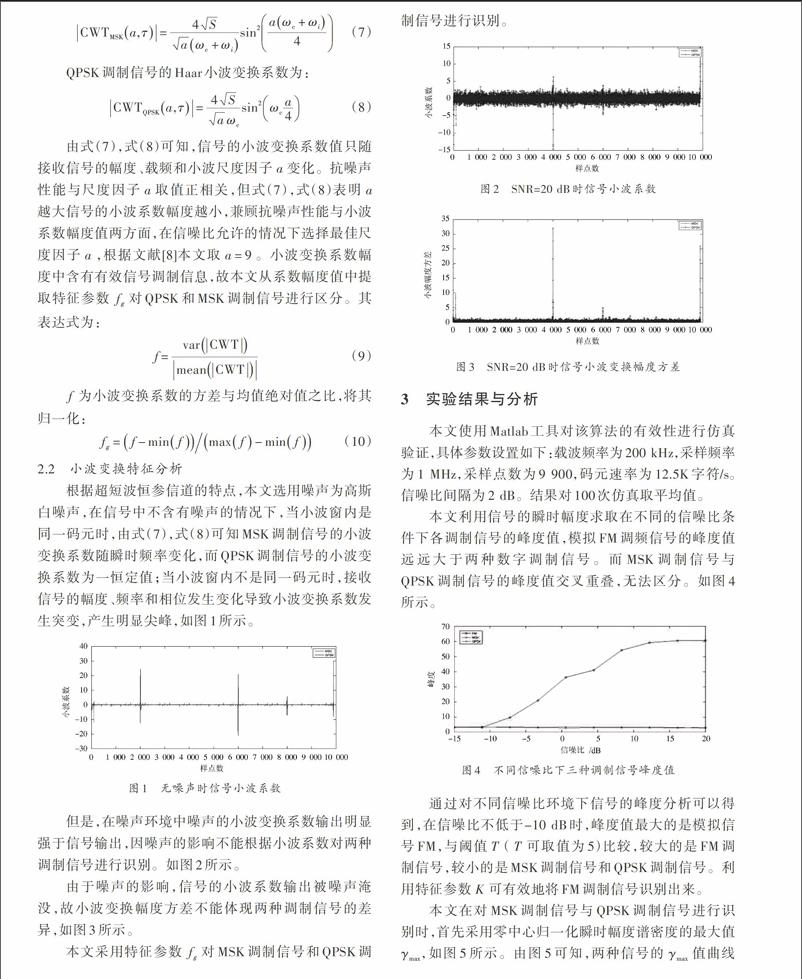
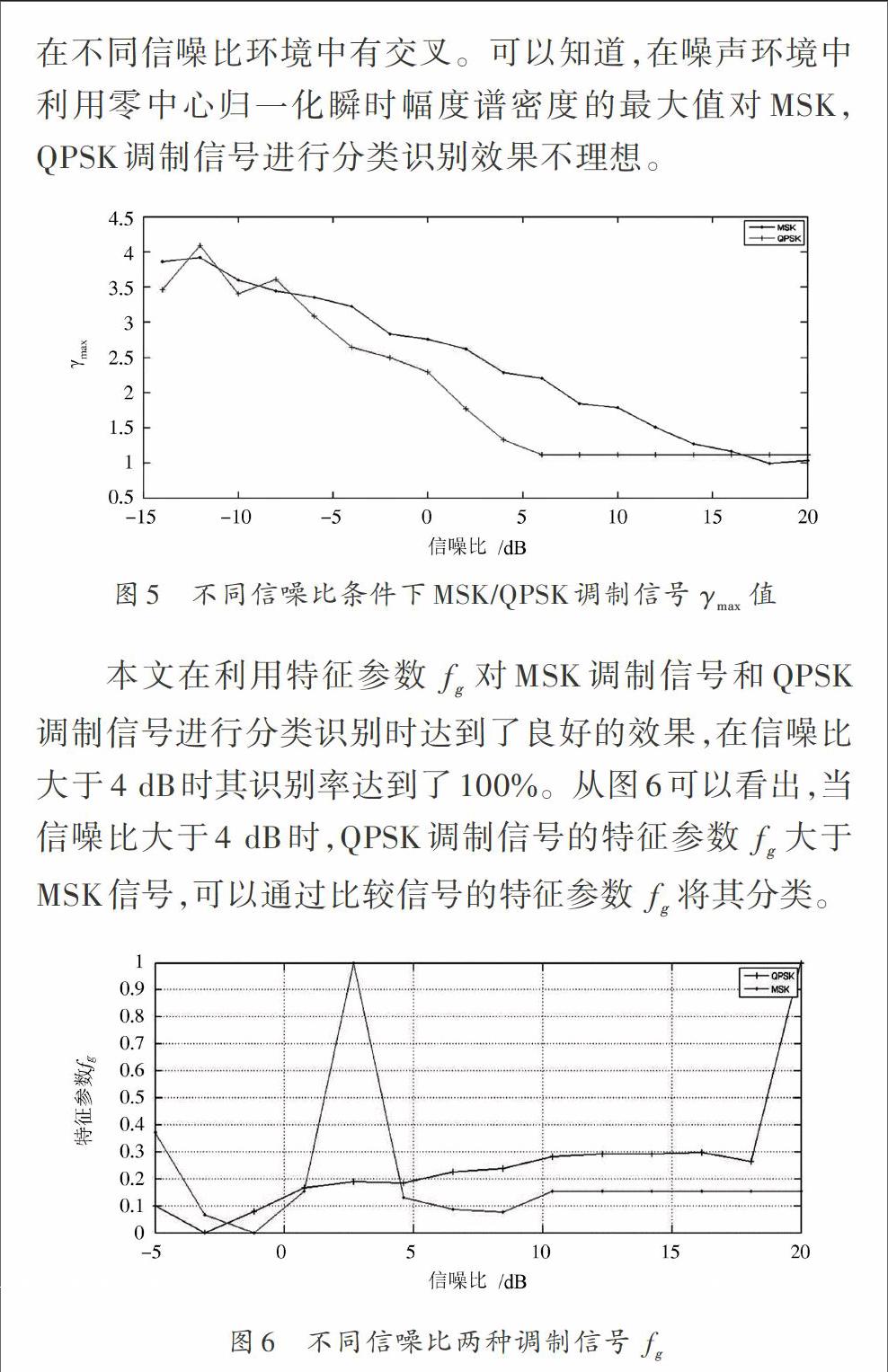
本文首先采用信号瞬时统计特征量零中心归一化瞬时幅度谱密度的最大值 [γmax]和小波变换幅度方差[5][VARWT]对三种调制方式分类识别，但分析表明，在噪声干扰环境下对信号的识别效果下降。针对上述问题，本文提出利用统计特征量峰度[K]和小波变换系数的方差与均值绝对值之比[fg]对三种调制信号进行分类识别。峰度是统计中描述数据分布形态的一项指标。在统计中，常以正态分布曲线为标准来比较某一随机分布的顶峰的尖平程度。峰度一般有三种表现形态：标准峰度、尖顶峰度和平顶峰度。正态分布曲线的峰度值[K=3]。分布曲线与正态分布曲线相比较，集中则为尖峰峰度，平稳则为平顶峰度。特征参数[K]反映曲线峰度，可用于判断信号是否具有数字基带信号特征[6]。数字调制方式信号的[K]值应有一个变化范围[ε

特征参量[fg]由信号小波变换系数方差与均值的绝对值之比得到。小波分析是将函数分解为“基本函数”之和，“基本函数”由小波函数经过伸缩平移得到。小波变换被誉为“数学显微镜”，具有良好的局部和整体分析能力，对非平稳信号具有良好的检测能力，它是一种理想的瞬态特征分析和提取工具。特征参量[fg]可以将MSK调制信号和QPSK调制信号识别分类。在信号识别之前，首先将信号进行功率归一化，保证提取的特征参数不因信号的功率造成影响。本文采用决策树方法分类识别，其识别流程为：

（1） 根据峰度[K]的大小识别出FM调制方式：峰度[K]值大的为FM调制信号，峰度[K]值小则为MSK和QPSK调制信号；

（2） 在不同信噪比条件下比较特征参量[fg]的大小：大的为QPSK调制信号，反之则为MSK调制信号。

4 结 语

本文首先指出几种对FM模拟调制与MSK/QPSK数字调制信号分类识别方法的不足，再对比零中心归一化瞬时幅度谱密度最大值[γmax，]提出先利用统计参数峰度[K]将模拟与数字调制信号识别开，然后利用小波变换特征参数[fg]将MSK/QPSK调制信号分开。在噪声环境中该方法具有更优的识别效果和更高的识别率。

参考文献

[1] 曾创展，贾鑫，朱卫纲.通信信号调制方式识别方法综述[J].通信技术，2015，48（3）：252?257.

[2] 张志民，欧建平，皇甫堪，等.数字和模拟通信信号调制方式的自动识别[J].国防科技大学学报，2010，32（4）：88?93.

[3] 马兆宇，边东明，张更新.通信信号调制识别方法简析[J].军事通信技术，2012，33（3）：39?44.

[4] 王蒙.通信信号调制识别与参数估计关键技术研究[D].郑州：解放军信息工程大学，2013：12?13.

[5] 杨杰，刘珩，卜祥元，等.通信信号的调制识别：原理与算法[M].北京：人民邮电出版社，2014：24.

[6] 任谦.基于软件无线电的调制方式自动识别[D].北京：北京工业大学，2013：30.

[7] ADDISON P S. The illustrated wavelet transform handbook [M]. Dublin： Science Engineering Medicine & Finance Institute of Physics Publishing， 2002.

[8] 魏小薇，曹志刚.低信噪比下数字幅度调制的调制进制快速识别[J].清华大学学报，2006，46（1）：35?38.