基于互信息和小波变换的图像配准的研究
2016-11-16罗志娟
罗志娟

摘要:该文提出了一种基于互信息和小波变换的图像配准算法,利用小波分解图像的近似分量和层层迭代算法进行配准,采用互信息作为图像相似性度量的准则,通过Matlab实验证明了该算法的有效性。
关键词:图像配准;互信息;小波变换
中图分类号:TP309 文献标识码:A 文章编号:1009-3044(2016)25-0197-03
Abstract: This paper presents an image registration algorithm based on gray level information and wavelet transform, the approximate component and layer iteration algorithm of wavelet decomposition was used for image registration,mutual information was used for similarity metric. The effectiveness of the proposed algorithm is proved by Matlab.
Key words: Image Registration; Mutual Information;wavelet transform
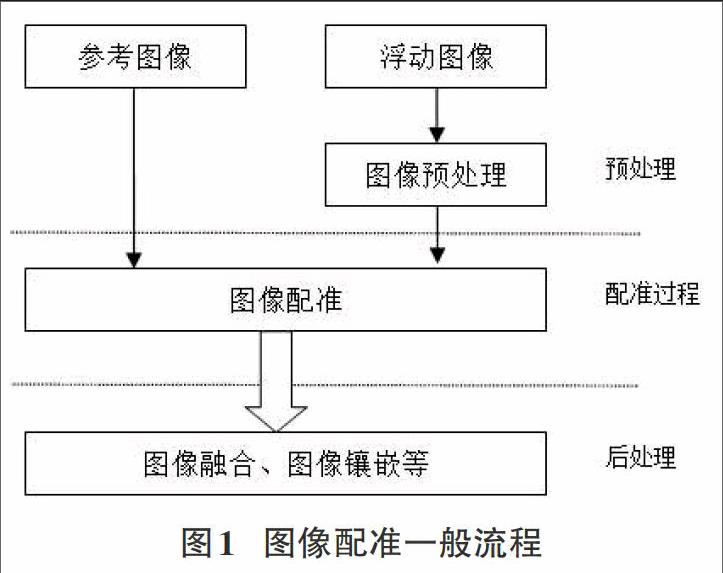
图像配准是近年发展迅速的图像处理技术之一,图像配准的主要任务是把两幅存在位移偏差的图像,将其中一幅图片经过平移、旋转、缩放等空间几何变换之后,使两副图像实现最佳对准。[1]在配准的过程中,通常取其中的一幅图像作为配准的基准,称之为参考图像,而实施空间几何变换的图像,称之为浮动图像。在通常的配准过程中,首先在参考图像中选取某一初始点为中心的图像子区域,视为图像配准的目标区域,接着让目标区域在浮动图像上有规律的移动,同时与浮动图像的相应区域进行对比,反复执行此过程,直到找到符合相似性度量要求的最优配准参数为止。现实生活中由于受诸多因素的影响,同一目标即使在同一时刻的两幅成像图像也不可能完全一致,配准也只能达到一定程度的相似。图像配准是图像融合、图像镶嵌等技术的基础,配准技术对图像的后处理尤为重要。图像配准的一般流程如图1所示。
图像配准技术一般包括基于图像特征和基于灰度两大类配准方法。基于特征的方法通常具有操作简单、速度快、精度较高等优势,但需要人工干预且特征点难以获取。而基于灰度的配准方法能实现完全自动的配准,且配准结果只依赖于配准算法本身,避免了主观因素带来的误差,但计算量大、耗时长。
配准算法在速度和精度上的矛盾制约着配准技术的发展。将信息论中的互信息作为配准度量可以使配准精度提高,小波技术凭借其在空间和频域上具有的良好局部特性及较高分辨率等优势,对小波分解后的子图样进行配准,可以使配准速度提高。[2]配准算法中同时采用互信息及小波技术可以有效地解决配准在速度和精度上的矛盾,大大提高配准算法的有效性和可行性。
1 互信息
互信息理论认为如果两幅图像完成配准,则它们之间的互信息将达到极大值[3]。最大互信息法通常作为相似性度量来对变换结果进行评估,为配准搜索下一步策略提供判优依据。两幅图像和的互信息定义如下[3]:
其中,和分别是和的平均信息量,是它们的相关平均信息量。根据互信息理论当达到最大值时,图像和就完成配准了。
2 小波变换
小波变换是在傅立叶变换基础上发展起来的,它不仅能在频域上进行分解,而且还可以在时域上对信号进行分解,且小波系数与原始图像存在着空间上的对应关系。[4]
把图像看作二维矩阵,大小为 N×N,经过一次小波变换后,图像便分解为4个子块频带区域,如图2所示。在经过3次小波分解后,LL3频带尺寸缩小为原尺寸的1/64,如图3所示。从图4的两幅图像对比可以看出,3次小波变换后图像与原始图像两者之间的空间分布具有良好的对应关系。图像数据能量集中在LL3子频带,可近似于图像内容的缩略图。
文献5指出,对两幅图像的空间几何变换配准,可转化为分别对两幅图像作小波分解,然后取两幅图像的近似分量实行空间几何变换配准。分解后的近似分量图像的伸缩和旋转系数与原图像配准时的伸缩和旋转系数相等,而近似分量图像的平移量是原图像平移量为的1/2,故上一层分辨率的平移分量优化初值要在每步优化后得到的初配准结果中的平移分量基础上乘以2。根据此原理,可以减少配准过程中的计算量,缩减配准时间。
3 配准算法实现
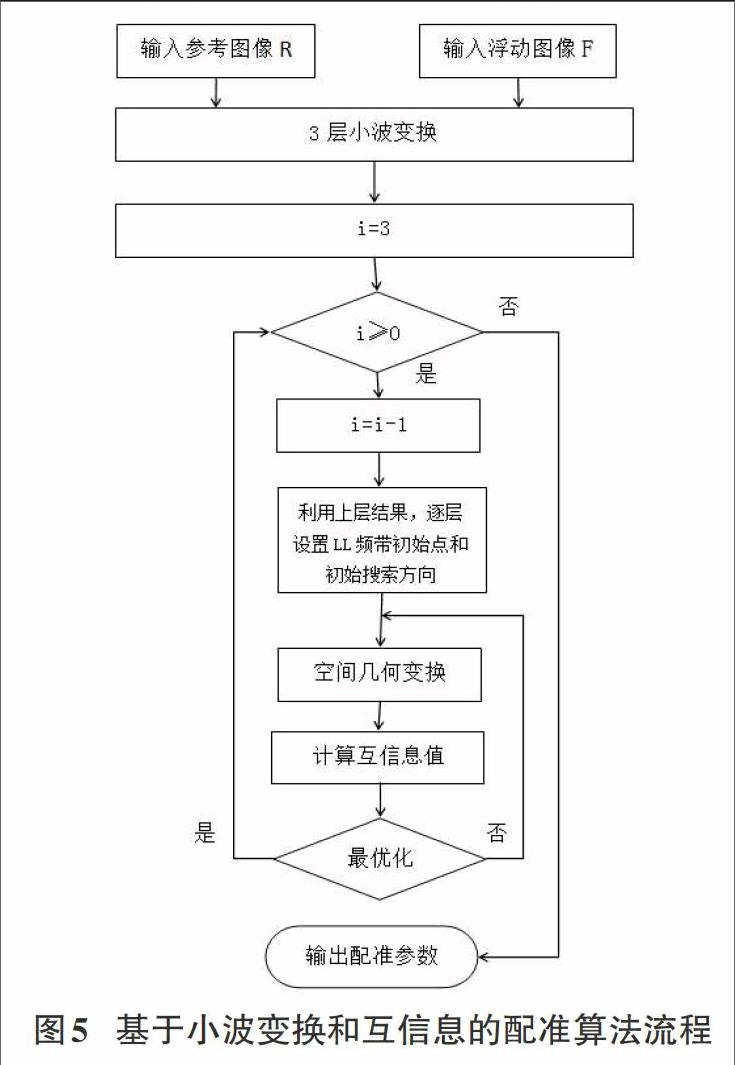
结合互信息和小波变换的优势,本文提出了一种基于互信息和小波变换的配准算法。利用层层迭代算法对小波分解图像的近似分量进行配准,计算出互信息值,作为衡量图像相似性度量的准则,来评估变换结果,为下一步搜索策略提供依据。
配准算法具体实现过程为:首先对参考图像R和浮动图像F分别进行3层小波变换;接着逐层进行搜索,选择两幅图像中的各层LL频带中尽可能接近的匹配点作为初始点,对LL频带实施空间几何变换,计算R和F的互信息值;然后利用Matlab7.1提供的fminsearch函数在初始点附近不断搜索使R和F互信息最大的点。在搜索的过程中每层都不断重复“空间几何变换计算互信息值最优化判断”的过程,直到搜寻到符合精度要求的参数为止。算法具体流程实现如图5所示。
4 实验结果及分析
在验证算法的可行性时,利用Matlab7.1平台完成实验,参考图像R和浮动图像F选用的都是256*256的灰度图像,如图6所示。图7为经过平移旋转后得到的配准图像。
程序运行结果如下:
x= [3.273 5.156 -5.367]T
fmax=4.6729
cMI=536
Elapsed time is 89.54869 seconds.
其中,x矩阵分别表示向上平移尺度、向右平移尺度、顺时针旋转尺度,fmax是参考图像和经空间几何变换后的浮动图像之间的最大互信息值,cMi是计算互信息的次数。
程序运行结果表明,此次配准中,浮动图像F按逆时针旋转5.367°,向上平移3.273pix,向右平移5.156pix,浮动图像与参考图像的互信息达到最大值4.6729,计算互信息的次数为536,耗时89.54869秒完成整个配准。仔细观察配准后图像,不难发现配准后图像没有重影且清晰可辨,达到配准效果。
5 结束语
配准精度高是互信息配准算法的优势,但庞大的计算量,制约了配准的速度[6]。因此,本文提出的算法先对图像实施小波变换,然后对小波分解图像的近似分量采用层层迭代算法进行配准,减少了数据计算量,配准时间大大缩减。从实验结果可知该配准算法能有效的实现图像配准,不论从精度还是速度上都能满足图像配准要求,该算法是行之有效的。但本文算法中的初始点和初始搜索方向等参数还可以进一步优化,以期提高算法效率。
参考文献:
[1] 陈显毅. 图像配准技术及其MATLAB编程实现[M].北京:电子工业出版社,2009.
[2] 赵钰,朱俊平,亢娟娜. 改进的区域互信息和小波变换的图像配准[J].计算机工程与应用,2012(6).
[3] Chen H M,Varshney P K,Arora M K. Performance of Mutual Information Similarity Measure for Registration of Multi-temporal Remote Sensing Images. IEEE Trans on Geoscience and Remote Sensing,2003,41(11):2445-2454.
[4] Zavorin I,Le Moigne J.Use Of Multiresolution Wavelet Feature Pyramids For Automatic Registration of Multisensor Imagery [J].IEEE Trans Image Process,2005,14(6):770-782.
[5] 刘斌,彭嘉雄.图像配准的小波分解方法[J].计算机辅助设计与图形学学报,2003,15(9):1070-1073.
[6] 夏倩倩,宋余庆. 结合分水岭和互信息的医学图像自适应分割方法[J].计算机应用与软件,2015(1).
