保持细节的Retinex红外图像增强算法

王坤

摘 要

本文首先讨论红外图像的特征，针对单一的直方图均衡的红外图像增强方法存在红外图像细节部分不能很好的保持甚至丢失的缺点，针对此缺点，对小波变换理论及Retinex算法进行了深入研究，提出一种保持红外图像细节的Retinex算法，并对其算法的实现过程和思路作了详细的描述，进一步通过MATLAB仿真，结果显示，该算法可以有效提升红外视频图像的细节信息。

【关键词】红外图像 图像增强 小波变换 直方图均衡 Retinex 细节保持

1 引言

红外图像反映了目标和背景的红外辐射的空间分布，其辐射亮度的分布主要是由所观测景物的温度和发射率所决定的。所观测景物温度高的部分表现在红外图像直方图上为灰度值大的部分，所观测景物温度低的部分表现在红外图像直方图上为灰度值小的部分。因此，红外视频图像近似反映了所观测景物的红外辐射空间分布、景物温差或辐射差。

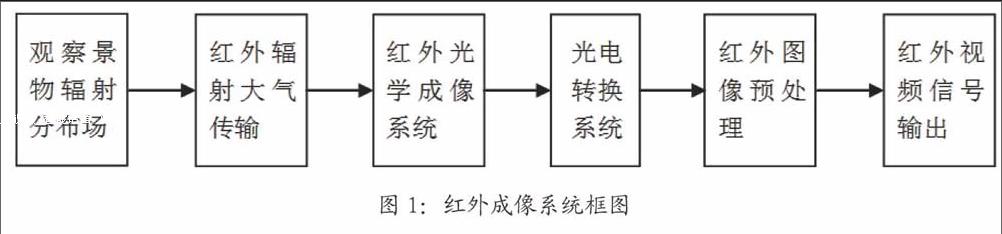
由图1红外成像系统框图所示，所观测景物的红外辐射需经过大气传输、光学成像、光电转换和预处理等过程才被转换为红外视频图像。因此红外图像一般表现为信噪比低、背景、目标对比度低，边缘模糊及细节表现差等特点。随着对红外图像增强效果要求的提高，保持原有红外图像细节信息以便更好地适应计算机分析和处理。

直方图均衡化在增强对比度的同时，也放大了噪声，并且造成图像信息的丢失；小波变换能将红外图像的高、低频信号很好地进行分离，而高频信号往往表示的是红外图像的细节信息和噪声；Retinex理论是基于特征的对比度增强方法，能将红外图像的目标部分进行增强处理且能有效抑制噪声。

2 红外图像的小波分解与Retinex基本理论

2.1 红外图像的小波分解

在小波域中，噪声主要存在于小尺度信号中，且随着分析尺度的不断增大而快速下降；而边缘细节部分，随着分析尺度的增大其下降速度比噪声慢。因此，采用多尺度多分辨率小波变换，提取红外图像多个维度上的小波系数，低频小波系数表征图像的轮廓信息，而图像不同维度上的细节、边缘以及噪声等信息则由其余的高频小波系数表征。

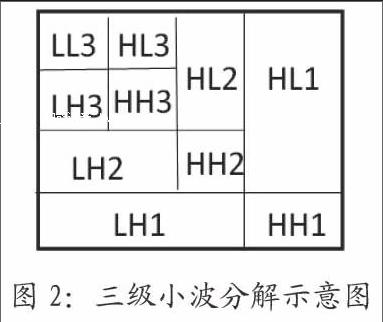
小波变换将图像分解成4个子带图像，水平与垂直方向皆为低频成分的LL；水平方向低频、垂直方向高频成分的LH；水平方向高频、垂直方向低频成分的HL；水平与垂直方向均为高频的HH。如图2所示。高频信号表示红外图像的细节信息及噪声信息。

2.2 Retinex基本理论

Retinex（视网膜Retina和大脑皮层Cortex的缩写）理论是于1971年提出的一种色彩理论。根据Edwin Land提出的Retinex理论，一幅给定的图像S（x，y）分解成两幅不同的图像：反射物体图像R（x，y）和入射光图像L（x，y） 。用公式表示为：

S（x，y）=R（x，y）×L（x，y） （1）

D Jobson等人提出了多尺度Retinex算法，其公式为：

（2）

其中，Ri（x，y）是Retinex的输出，i∈R，G，B表示3个颜色谱带，红外图像由于是灰度图像i只取其灰度值。Fn（x，y）是高斯滤波函数，Wn表示尺度的权重因子，N表示使用尺度的个数，N=1表示灰度图像即红外图像。

3 保持细节的Retinex红外图像增强算法

红外图像是展现物体的热量分布状态明暗交替的灰度图像，具有信噪比低、背景、目标对比度低，边缘模糊及细节表现差等特点。根据红外图像的这些特点以及对直方图均衡、小波变换和Retinex算法的分析，本文的保持细节的Retinex红外图像增强算法综合三种算法的优点。

由于小波变换可以将红外图像分解为低频子带图像和高频子带图像，红外图像的细节部分保留在高频子带图像中，在Retinex算法中可以将噪声有效过滤，因此可以用Retinex算法对高频部分进行增强，获得能够保留红外图像原始细节信息的高频部分增强图像，且能够有效的过滤噪声。对于低频部分图像，将用直方图均衡算法进行对比度增强，以使红外图像的对比度相较于完全使用Retinex算法或小波变换算法增强的红外图像较高。

低频部分采用直方图均衡化的过程如下：

（1）列出低频部分原始红外图像的灰度级rk；

（2）统计低频部分原始红外图像直方图灰度级像素数nk；

（3）计算低频部分原始直方图个概率：pk=nk/N（k=0，1，2，...，L-1）；

（4）计算累计直方图sk=∑pk；

（5）取整Sk=int{（L-1）Sk+0.5}；

（6）确定映射对应关系：rk→sk；

（7）统计新直方图各灰度级像素nk；

（8）用pk（sk）=nk/N计算新直方图。

高频部分采用Retinex算法的过程如下：

（1）利用取对数的方法将照射光分量和反射光分量分离

S（x，y）=r（x，y）+l（x，y）=log（R（x，y））+log（L（x，y））

（2）用高斯模板对原始图像做卷积，得到低通滤波后的图像D（x，y），F（x，y）表示高斯滤波函数

D（x，y）=S（x，y）*F（x，y）

（3）在对数域中用原始图像减去低通滤波后的图像，得到高频增强图像G（x，y）

G（x，y）=S（x，y）-log（D（x，y））

（4）对G（x，y）取反对数，得到增强后的图像R（x，y）

R（x，y）=exp（G（x，y））

（5）对R（x，y） 做对比度增强，得到最终的高频部分增强后的图像。

原始红外图像与直方图均衡红外增强图像、小波分解红外增强图像和本文算法红外增强图像效果图如图3、图4、图5和图6所示。

4 结论

本文针对红外图像对比度低、细节部分表现差等特点，利用小波变换将红外图像分解为高、低频部分，对包含红外图像细节部分的高频部分进行Retinex算法增强，可以有效的保留原始红外图像的细节信息，且能够有效的抑制噪声；对红外图像的低频部分进行直方图均衡化增强，保留直方图对红外图像的对比度增强的优点。因此，本文算法一定程度地使红外图像的对比度增强，且有效抑制噪声的同时可以保留原始红外图像的细节信息。

参考文献

[1]赵小川.MATLAB图像处理-程序实现与模块化仿真[M].北京：北京航空航天大学出版社，2014.

[2]温海滨，毕笃彦等.消除光晕和细节增强的多尺度Retinex红外图像增强[J].红外技术，2016.

[3]李毅，张云峰等.尺度变化的Retinex红外图像增强[J].液晶与显示，2016.

[4]郝建新.基于小波变换与Retinex的电路板红外图像增强技术[J].红外技术，2015.

[5]刘辉，赵文杰等.改进的多尺度Retinex红外图像增强算法[J].计算机技术与发展，2011.

[6]Rafael C.Gonzalez，Richard E.Woods，Steven Eddins.Digital Image Processing Using MATLAB[M].北京：电子工业出版社，2005.

[7]李毅，张云峰等.基于子带分解多尺度Retinex的红外图像自适应细节增强[J].中国激光，2015.

[8]邓亚平，王敏.基于视觉注意机制的红外弱小目标检测[J].华中科技大学学报（自然科学版），2015.

[9]代少生，刘琴等.基于路径的Retinex算法在红外图像增强中的应用[J].半导体光电，2015.

[10]李毅.基于视觉模型的红外图像增强技术研究[D].长春：中国科学院长春光学精密机械与物理研究所，2016.

[11]王忆锋.红外图像灰度直方图统计分析的研究[J].红外，2009，4（30）：14-16.

[12]彭真明，雍杨，杨先明等.光电图像处理及应用[M].成都：电子科技大学出版社，2008.

[13]于雷.红外图像预处理算法研究及硬件实现[D].南京：南京理工大学，2010.

[14]尹士畅，喻松林.基于小波变换和直方图均衡的红外图像增强[J].激光与红外，2013，43（02）：225-228.