一道高中联赛预赛题的多解与拓展



一道高中联赛预赛题的多解与拓展

浙江省金华市第六中学(321000)虞懿

2014年陕西数学联赛预赛题：

如图1，已知圆O:x2+y2=1与x轴交于A、B两点，与y轴交于点C,M是圆O上任意一点(除去圆O与两坐标轴的交点)．直线AM与BC交于点P,直线CM与x轴交于点N,设直线PM、PN的斜率分别为m、n,求证：m-2n为定值．

1.解法呈现

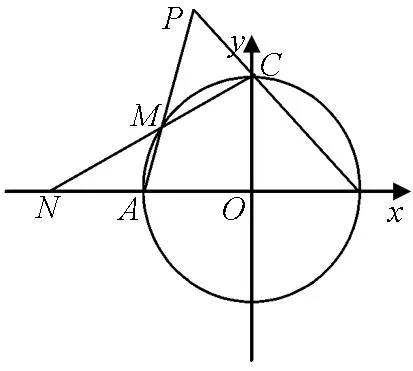
图1

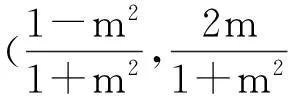
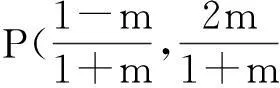
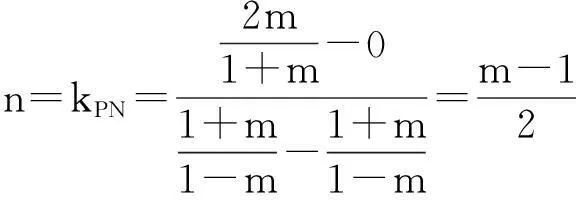
故m-2n=1(定值)．

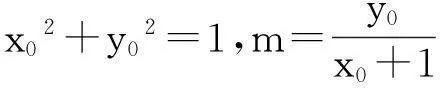
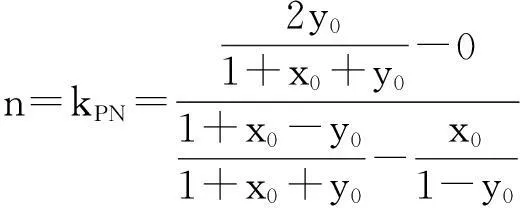
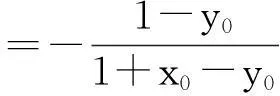
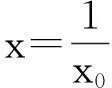
2.一般推广

回顾此题，定值m-2n=1恰好是直线BC(或PB)斜率的相反数，即有kPA+kPB=2kPN,此结论是否具有一般性呢？为了减少推理运算的盲目性，笔者用几何画板对满足上述信息的问题进行了一番演示，意外地发现，当直线PB与圆O的交点不在y轴上，则有：

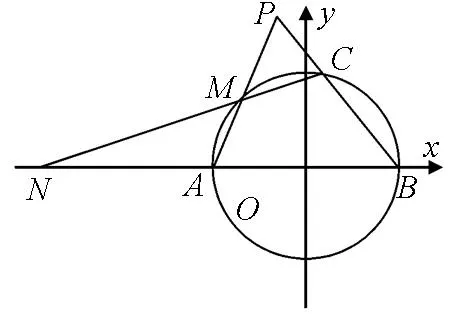
图2

结论1如图2，已知圆O:x2+y2=r2与x轴交于A、B两点(点B在点A右侧)，x轴上、下方有不在圆O上的动点P,设直线PA、PB与圆O的另一个交点分别为M、C,直线CM与x轴相交于点N,若直线PA、PN、PB的斜率存在，则kPA+kPB=2kPN.

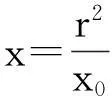
3.变式拓展

一道好的试题往往是命题者研究成果的结晶，在同一个背景下，交换部分条件和结论，或给出某个问题一般结论的特例，便生成出一道新题，又能挑战你的思维．笔者结合对相关题目的研究，又做了如下拓展：

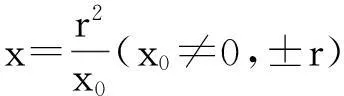
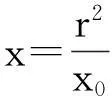
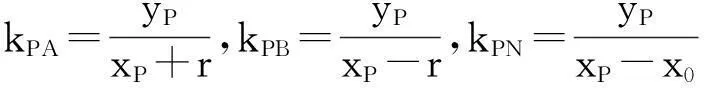
结论4已知圆O:x2+y2=r2与x轴交于A、B两点(点B在点A右侧)，x轴上有一定点N(x0,0)(x0≠0,±r)，不在x轴上的动点P，使得直线PA、PN、PB的斜率存在且满足kPA+kPB=2kPN,设直线PA、PB与圆O的另一个交点分别为M、C.求证：N、M、C三点共线．

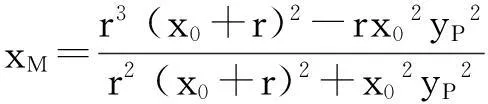
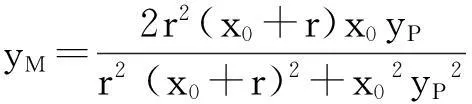
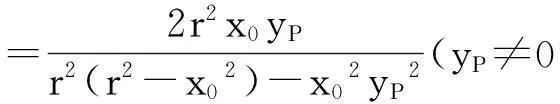
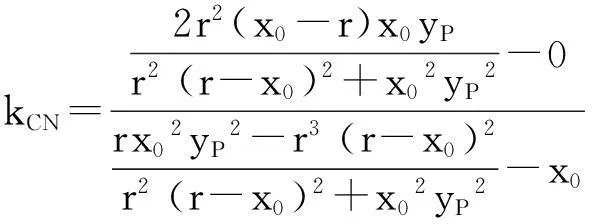
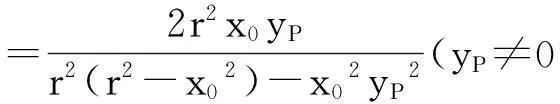
于是kMN=kCN,则N、M、C三点共线．上述结论对椭圆、双曲线、抛物线是否成立呢？留给有兴趣的读者去探究．

4.体会浅说

通过以上的探究过程，笔者感悟到对于任何问题都要多思、多想、多问为什么，这样数学会因思考而更加精彩，一道优秀的试题是要经过多思善想，这样才会有惊喜和收获．在学习中要学会用抽象、类比和变式去研究数学问题，更重要的是可以提升数学品质和数学素养，既需要大胆的猜想和细心的求证，还需要坚定的意志和灵活的变通，所以说，只有多思、多想、多变，才会有创新、发现和收获．