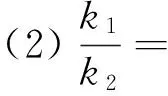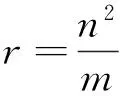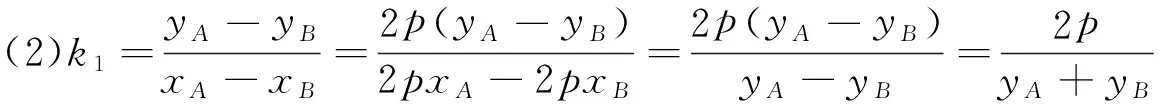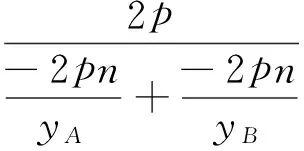圆锥曲线的一组统一性质

张　寅

湖南省桃江县第一中学　(413400)　胡芳举湖南省桃江县职业中专　(413400)



圆锥曲线的一组统一性质

张寅

湖南省桃江县第一中学(413400)胡芳举湖南省桃江县职业中专(413400)

本文将给出圆锥曲线的一组美妙性质.

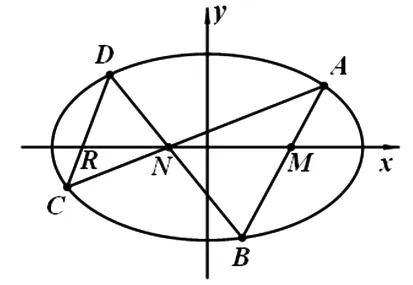
图1

定理1如图1，已知曲线(椭圆或双曲线)ax2+by2=1及两定点M(m,0)、N(n,0)(M,N不在曲线上)，动弦AB过点M，直线AN、BN分别交曲线于点C、D，设直线AB、CD的斜率分别为k1、k2(k1k2≠0)，则

(1)直线CD过定点R(r,0)；

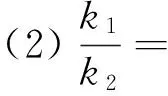
证明：(1)由k1k2≠0知：A、B、C、D四点都不在x轴上.

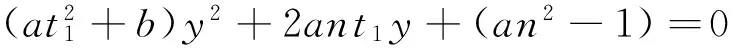
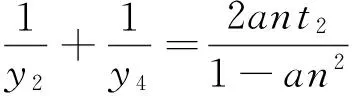
由A(x1,y1)、B(x2,y2)、M(m,0)共线得

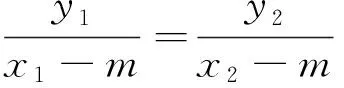
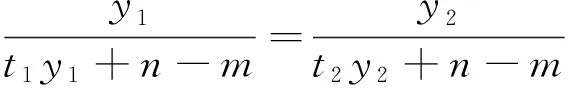
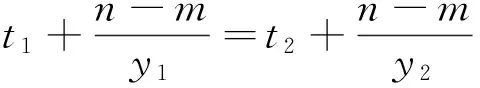
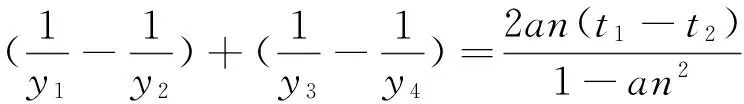
由于a,m,n为定值，故r为定值，所以直线CD过定点R(r,0).

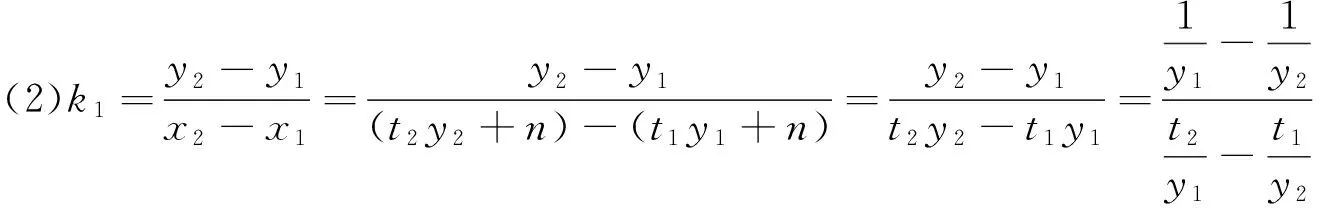
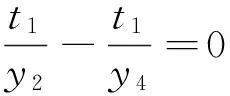
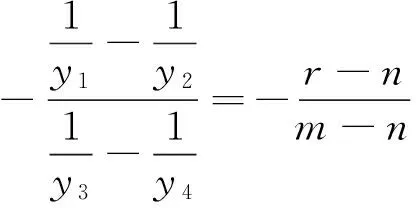
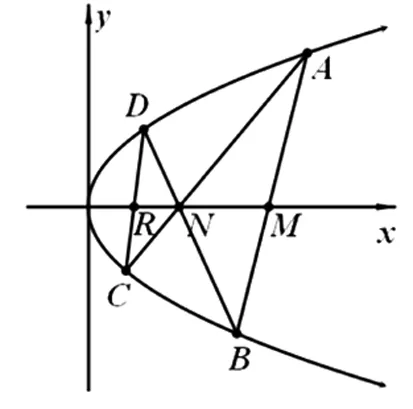
图2

定理2如图2，已知抛物线y2=2px(p>0)及两定点M(m,0)、N(n,0)(M,N不在抛物线上)，动弦AB过点M，直线AN、BN分别交抛物线于点C、D，设直线AB、CD的斜率分别为k1、k2(k1k2≠0)，则

(1)直线CD过定点R(r,0)；