合理定位变量 有效解决双变量最值问题



合理定位变量有效解决双变量最值问题

江苏省常州市奔牛高级中学(213131)狄闻于

近几年各个省份对二元变量求最值问题的考察非常频繁，这些问题式子繁，难度大，综合性强，涉及到函数、不等式、线性规划、解析几何及导数等诸多高中数学重点知识，更体现了函数思想、转化化归思想及数形结合等若干核心数学思想的应用.学好二元变量最值的求解是函数部分的一大重点.

让我们先来看一组典型例题：

例1(1) 不等式ax2+4x+a>1-2x2在x∈R上恒成立，则a的范围是多少？

(2)不等式ax2+4x+a>1-2x2对|a|≤2的所有a恒成立，求x范围是多少？

这是我们经常遇到的两道二元变量的不等式恒成立问题.

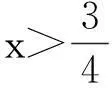
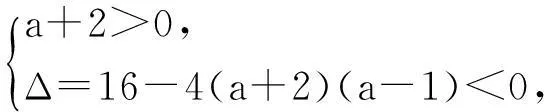
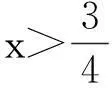
从以上两题可以看出题中的变量与参数是相对而言的，只是不同的题目，不同的情况而已，一般我们可以总结为给出谁的范围，谁就是主元，要求谁的范围，谁就是参数，这样便能领悟双变量问题的真谛，迅速解决问题.平时的教学既要注重知识教学，更要注重能力培养，在引导学生对典型问题分析，讨论的过程中尤其要注重方法与技能的概括与总结，这样才能有效提升学生的数学思维能力.下面让我们再看一例.

这是一道典型的二元变量求最值问题，仔细分析问题，发现a,b间无等量关系，常规的一些方法，如消元，基本不等式，线性规划都解决不了问题.若a,b都在变，则最值很难研究.我们不妨定一个，动一个，即一个看做变量，另一个看做参数.

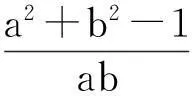
以上解双变量问题的核心思想为定一变一，即确定一个为主元，另一个为参数，这样就可以构造函数，利用函数思想来解决问题，所以合理定位主元，参数是打通解题通道的关键.

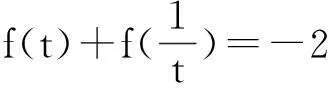
解析：此题表面看上去有四个变量x,a,b,t ，但只要将问题与已有条件结合起来，便可顺利转化，学习和掌握等价转化思想有利于我们从更深刻层次去揭示数学知识和方法的内在联系，从而提高分析问题，解决问题的能力.

通过我们发现题目所给的条件越来越精炼，没有了明显的提醒，这就对学生的能力提出了更高的要求，所以我们需要对变量仔细解读，然后合理的定位，从而解决双变量最值问题.