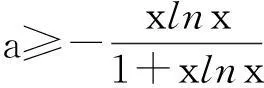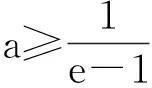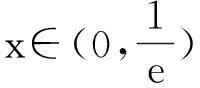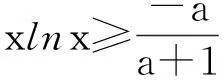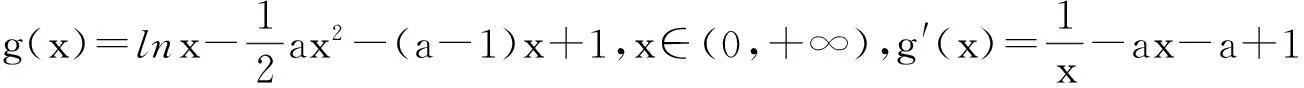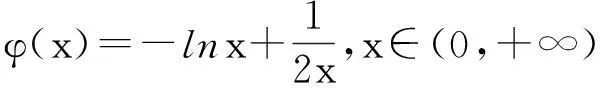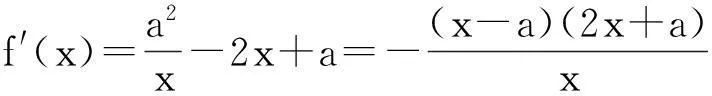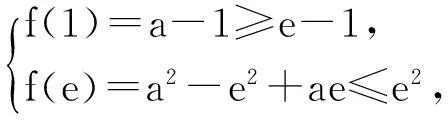缩小参数范围优化“恒成立问题”的处理



缩小参数范围优化“恒成立问题”的处理

安徽省阜阳市第三中学(236000)夏炳文

笔者所在的学校曾连续的两次调考中都考查了含参数不等式恒成立问题，在阅卷中发现学生处理此类问题时所采取的解题方法和方向基本上是没有问题的，但是由于在解题的过程中，解题策略不优化，导致不能够顺利得出正确结果，下面就恒成立问题处理的优化策略，笔者谈一下看法，与大家交流.

(1)当0

(2)是否存在实数a，使f(x)≤x恒成立，若存在，求实数a的取值范围；若不存在，说明理由.

限于篇幅，本文只考虑第(2)小题的作答.

阅卷中发现，学生的处理方法主要有以下两种：

通过以上解法基本上可以发现，学生在处理含参数不等式恒成立问题时所采取的方法基本上是正确的，即转化为求函数最值加以处理，并且求函数最值的手段有两种：一是直接求含有参数的函数最值；二是通过分离参数转化为求一个具体的函数的最值.通过这两种解法的对比不难发现，第一种转化的函数里面因为含有参数，所以在求其最值时可能会需要分类讨论，而第二种转化的函数虽然是个具体的函数，相比较容易求出其最值.但是这种方法也有其局限性，可能有些时候是不可以进行参数分离的，或者分离后所构造的函数虽然具体但形式过于复杂，同样导致解题的失败.

命题人给出的参考答案：

(2)f(x)≤x恒成立可转化为a+(a+1)xlnx≥0恒成立，令φ(x)=a+(a+1)xlnx，x∈(0,+∞)，则φ′(x)=(a+1)(1+lnx).

参考答案采取的是直接求含有参数的函数最小值进行处理，就是因为参数的存在，导致在求函数最值的时候需要进行分类讨论.

优化后的解法：

1.针对学生和参考答案采取的直接构造含参函数的方法，我采取了以下的优化：

2.针对第二种分离参数的方法，依然可以采取以上的优化方法：

通过以上两种方法的优化不难发现，在题目没有明确给出参数a的范围时，我们在处理问题时只能先认为a∈R,这样就会需要运用到分类讨论的思想，但是因为恒成立的不等式对所给变量范围内的任意一个数都满足，那么我们就可以先利用一些特殊值去缩小参数a的范围，从而在求函数最值时不需要或者减少分类讨论的情况.

(1)求函数f(x)的单调递增区间;

(2)若关于x的不等式f(x)≤(a-1)x-1恒成立，求a的最小整数值.

本文只考虑第(2)小题.

学生的处理方法以及遇到的问题同题目1.

命题人给出的参考答案：

参考答案是采取了分离参数的方法求函数最值，通过以上解法不难发现存在两个难点：一是转化后的函数形式过于复杂，学生不敢下手；二是在求所构造的函数最值时需要用到二次求导，所以此种解法难度较大.

优化后的解法：

此解法采取的也是直接求函数最值，但是通过代入特殊值后缩小了参数a的取值范围，从而使求解函数的最大值时不需要分类讨论，优化了解题过程.

无独有偶，2011年浙江省高考文科卷21题也是利用了此种方法优化了解题过程，试题如下：

设函数f(x)=a2lnx-x2+ax,a>0.

(1)求f(x)的单调区间;

(2)求所有实数a，使e-1≤f(x)≤e2对x∈[1,e]恒成立.注：e为自然对数的底数.

解法分析：如果没有利用f(1)=a-1≥e-1，那么第(2)问就需要对参数a按a≤1,1

恒成立问题是高中阶段非常重要的一个问题，综合性和灵活性较强，因而受到高考命题者的青睐，在试题中高频考查，高三复习应在掌握此类问题基本解法的基础上，再介绍适用技巧即通过利用特殊值首先缩小参数的范围，这样可以使问题的求解难度大大简化.