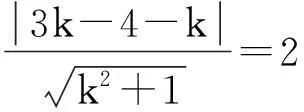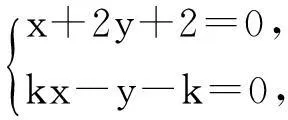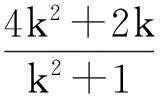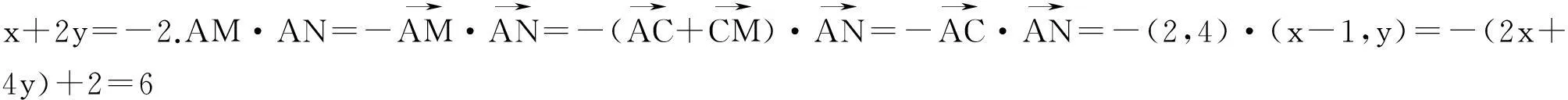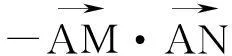解几中一类题不同的处理视角举隅



解几中一类题不同的处理视角举隅

江苏省苏州市吴县中学(215151)张文海

向量作为现代数学的重要基础进入高中数学知识体系后，不仅成为支撑数学学科知识体系的重点知识，也是研究许多重要数学问题强有力的工具之一.而“注重通性通法，淡化特殊技巧”、“在知识网络交汇点设计试题”是近几年来新高考命题的重要理念.本文拟从坐标、距离、向量三个角度分析处理解析几何中的一类向量数量积或线段之积问题的解法，以供复习参考.

一、从“坐标”的角度转化问题

平面向量具有代数与几何形式的双重属性，它融数形于一体，与解析几何的本质一脉相承，所以联系向量和解析几何的重要桥梁就是坐标，利用坐标解向量与解析几何的综合题是通性通法之一.

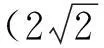
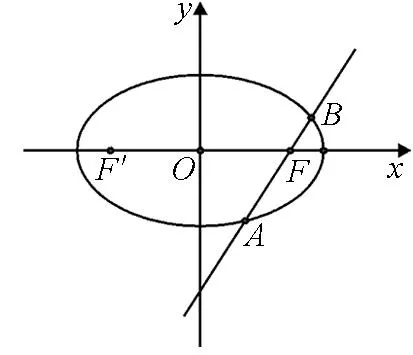
图1

(1)求椭圆C的方程；

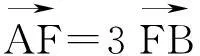
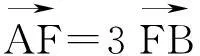
二、从“距离”的角度转化问题

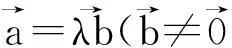
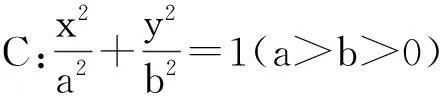
(1)若A为椭圆的下顶点，求椭圆的离心率e；

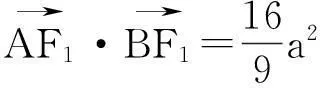
解：(1)略.

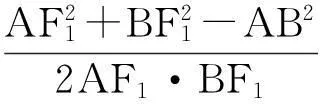
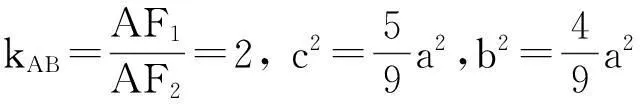
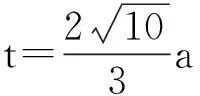
图2

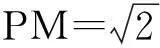
(1)试建立适当的坐标系，求动点P的轨迹E；

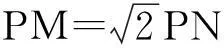
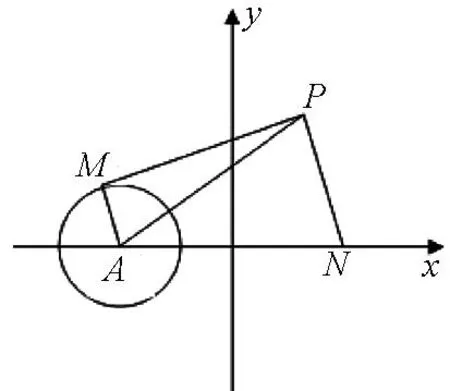
图3

(x+4)2+y2-4=2[(x-4)2+y2]，化简得(x-12)2+y2=124．

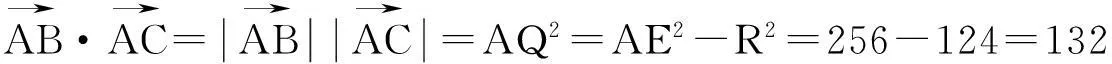
三、从“向量”的角度转化问题

圆锥曲线中的定值问题一直是高考的热点问题，由于定值一般没有给出，这类题不仅考查逻辑思维和综合运用知识的能力，还要具备较强的目标意识和转化与化归的能力．由于向量的模是数量，从而在解决线段长度问题时，可以通过把长度问题转化为向量问题进行优化处理．

例4设圆C:(x-3)2+(y-4)2=4，直线l1过定点A(1,0).

(1)若直线l1与圆C相切，求直线l1的方程；

(2)若直线l1与圆C相交于直线P,Q两点，线段PQ的中点为M，又直线l1与直线l2:x+2y+2=0的交点为N，求证：AM·AN为定值．

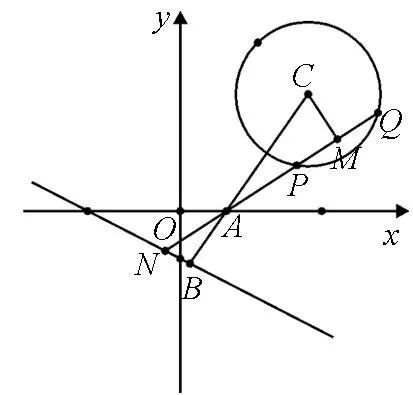
图4

解：(1)①若直线l1的斜率不存在，即直线l1的方程为x=1，符合题意．