一个不等式的多角度审视



一个不等式的多角度审视

广东省深圳市南头中学(518052)徐黄

题目对任意实数a>1,b>1有不等式

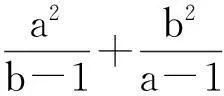
本文将从六个方面给出该不等式的证明．

1．利用恒等式

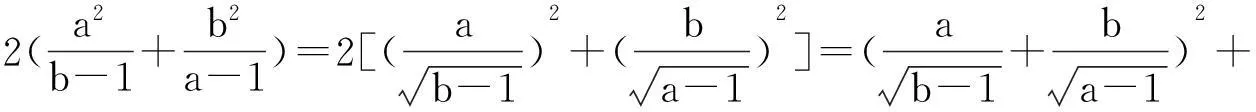
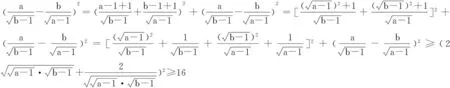
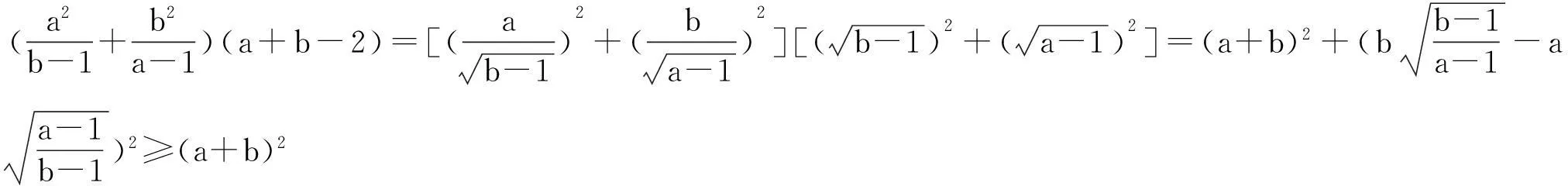
2．利用不等式

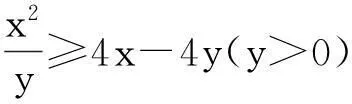
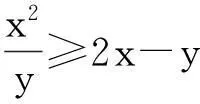
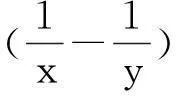
3．利用参数法

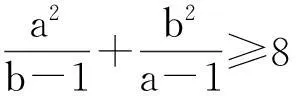
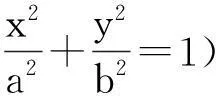
证明11:由完全平方式(a-t)2≥0，易得a2≥2at-t2，其中t为参数．

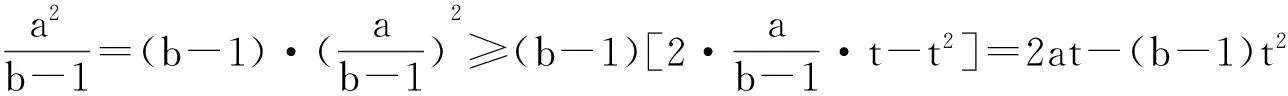
为使所证不等式成立，只须令2(a+b)t-(a+b)t2+2t2=8，易知t=2时成立，故当t=2时代入即得所要证明的不等式．

4．利用对偶式

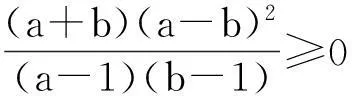
5．利用配方法

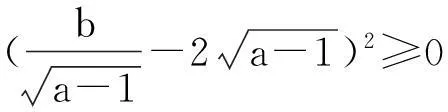
6．利用无穷递缩等比数列求和公式

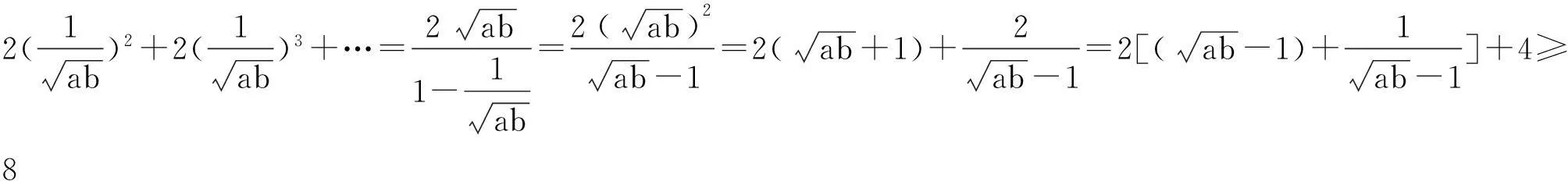
7．利用概率

证明15：设随机变量ξ的分布列为：

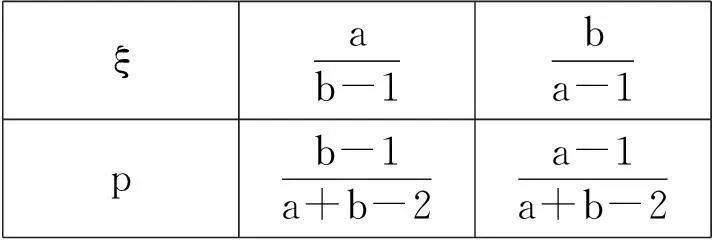
ξab-1ba-1pb-1a+b-2a-1a+b-2

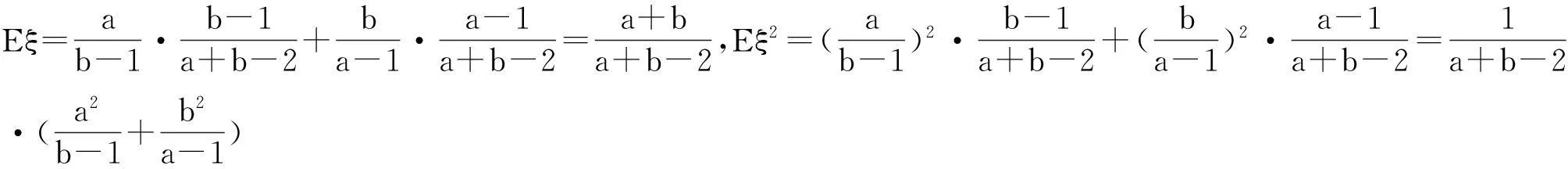
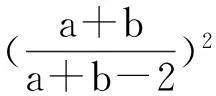
8．利用向量

以上从八个不同方面、不同角度给出了此不等式的16种证明方法，相信读者还会有更好、更多的方法．因此，我们在引导学生进行“一题多解，一题多证”的思维训练时，要让学生自觉地变换思维角度，多方位思考，多渠道辟径，这样就会越过思维障碍，从而极大的激发学生学习数学的兴趣和热情，进而提高他们的数学素养．

参考文献

[3]田彦武.用一不等式巧解一串竞赛题[J].中学数学研究(江西),2002，11.

[6]田彦武，马小林.巧用一个不等式求最值[J].数学教学,2005，5.