对称撞击下钢筋混凝土框架结构的非线性响应*

魏德敏　刘德源　李頔

(1.华南理工大学 土木与交通学院， 广东 广州 510640； 2.华南理工大学 亚热带建筑科学国家重点实验室，

广东 广州 510640)



对称撞击下钢筋混凝土框架结构的非线性响应*

魏德敏1,2刘德源1李頔1

(1.华南理工大学 土木与交通学院， 广东 广州 510640； 2.华南理工大学 亚热带建筑科学国家重点实验室，

广东 广州 510640)

摘要:对钢筋混凝土框架结构在集中对称撞击荷载作用下的非线性动力响应进行理论分析.分析中考虑了落锤初始撞击速度及梁柱线刚度比的影响，并通过非线性有限元分析得到撞击力随时间变化的规律、结构的位移响应和最终变形，确定了结构塑性变形的特性及耗能情况.通过分析计算结果，提出估算框架结构受撞击处最终变形的简化分析模型，进行了简化计算结果与有限元分析结果的对比，发现：相对于梁柱线刚度比，初始撞击速度对结构撞击响应的影响较大；框架结构的塑性变形主要集中在框架梁两端及跨中，且框架梁的塑性变形随着初始撞击速度的提高明显增大；框架柱有对称向外的水平位移，塑性变形相对较小.

关键词：钢筋混凝土框架结构；对称撞击；初始撞击速度；线刚度比；非线性动力响应；有限元分析

结构在短时强冲击荷载作用下将发生突然破坏，给人们的生命财产造成重大损失，因此工程结构的抗冲击性研究具有重要的理论意义和应用价值.由于结构冲击试验的技术难度较大，所需费用较高，以及尺寸效应的影响，因此关于结构冲击试验的研究成果相对较少.目前大多研究工作的思路是在构件层次或缩尺模型的试验结果基础上进行结构层次的非线性有限元分析计算，提出工程实用的简化分析模型.工程结构非线性冲击响应的分析以有限元法为主，研究的问题多为飞机、舰船、汽车的抗冲击性能[1- 5].关于钢筋混凝土结构在集中撞击下非线性响应的研究成果尚不多见.

张瑞坤等[6]对钢筋混凝土柱在侧向撞击作用下的动力响应进行了数值模拟分析，研究截面惯性矩、混凝土抗压强度、纵筋配筋率及箍筋间距对柱中节点位移的影响.在此基础上，文献[7]提出了钢筋混凝土柱在侧向冲击荷载作用下弯曲型变形与直剪型变形模型的动力反应简化计算公式.王兴国等[8]利用ANSYS有限元分析软件计算了混凝土框架结构在水平冲击荷载作用下的位移响应，得出在边柱不同位置撞击时框架结构最终变形的简化分析模型.刘锋等[9]基于大变形动力控制方程和有限差分法，对冲击荷载作用下框架结构的非线性动力响应进行了初步研究.于敏[10]采用数值模拟的方法模拟了某多层钢筋混凝土框架结构在第二层竖向构件失效后，上部结构撞击下部结构产生的结构落层倒塌响应过程.高菲[11]考虑了弹体作用位置、弹体撞击速度、混凝土强度、柱轴压比等因素，建立了二层二跨的钢筋混凝土空间立体框架，并对其进行了高速撞击下的动力分析.

1计算建模

文中研究的钢筋混凝土门式框架结构高度为3.0 m，跨度为4.0 m，混凝土标号为C30，框架柱截面尺寸为400 mm×400 mm，配置纵筋4A8，框架梁截面尺寸为200 mm×400 mm，梁顶纵筋为2B12，梁底纵筋为2C18，梁柱配置箍筋的间距一般为200 mm，在梁柱节点区域为100 mm.结构设计符合现行规范[13].

采用ABAQUS/EXPLICIT有限元程序进行分析.有限元分析建模时，框架梁柱的钢筋采用三维桁架单元T3D2和理想弹塑性本构关系.混凝土采用八节点减缩积分实体单元C3D8R和塑性损伤本构模型，该本构模型适用于模拟混凝土在单调、循环或者动载作用下的力学行为，相关参数为:剪胀角ψ=30°,流动势偏移量ε=0.1,双轴与单轴受压极限强度比σb0/σc0=1.16,不变量应力比Kc=0.667,粘滞系数μ=0.000 5.混凝土单元长度为50 mm，框架梁受撞击处的单元网格密度适当细化，单元长度为20 mm，为撞击体网格尺寸的一半[14]，共11 904个单元.钢筋单元长度为25 mm，共计3 196个单元，假设钢筋与混凝土之间没有相对滑移.撞击体与结构的接触为面面接触，接触面积为200 mm×200 mm.结构响应时程分析的时间步长取1×10-6s.

2有限元分析

假设质量m=400 kg的落锤对框架梁跨中垂直对称冲击，考虑初始撞击速度V0和框架梁柱线刚度比ib/ic变化对结构非线性响应的影响.

2.1初始撞击速度对结构响应的影响

图1和2分别给出了框架结构梁柱线刚度比ib/ic=0.375，而落锤的初始撞击速度V0在3.0～7.0 m/s范围内变化时，按一定比例放大的结构最终变形模态图及框架梁跨中挠度时程曲线.表1为框架梁跨中最大挠度Umax及其出现的时间Tu、最终挠度Ur、塑性耗能EPb的计算结果.图3为框架结构混凝土中的塑性应变分布，表1给出了结构和构件的耗能情况.

图1　框架结构最终变形

图2　框架梁跨中挠度时程曲线

Fig.2Time-history curves of the mid-span deflection of the frame beam

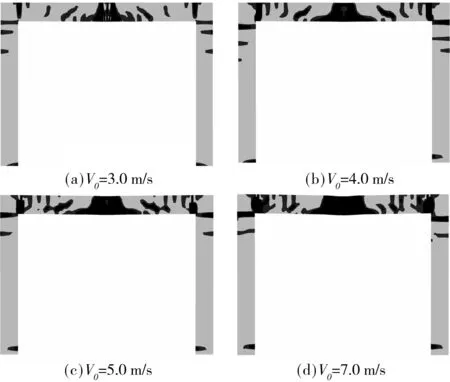
图3　结构中混凝土的塑性区

Table 1Dynamic responses of frame beam under different impact velocities

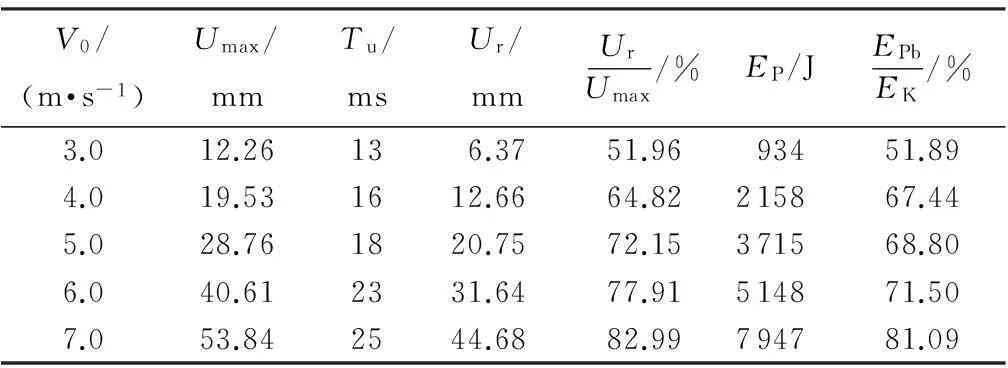
V0/(m·s-1)Umax/mmTu/msUr/mmUrUmax/%EP/JEPbEK/%3.012.26136.3751.9693451.894.019.531612.6664.82215867.445.028.761820.7572.15371568.806.040.612331.6477.91514871.507.053.842544.6882.99794781.09

由图2可知，在撞击初期(20 ms之内)框架梁跨中的挠度很快由0增加至最大值Umax，然后下降并逐渐稳定，框架梁跨中最大挠度和最终挠度Ur随着初始撞击速度的提高而增大，但最大挠度Umax出现的时间Tu有所推后.

由表1可知，落锤的初始速度V0提高时，框架梁跨中最大挠度和最终挠度，以及二者的比值Ur/Umax明显增大，框架梁的塑性耗能量EPb以及与初始撞击能量EK的比值EPb/EK也是随之增大的，因此框架梁的塑性变形及其所消耗的能量EPb均随着初始撞击速度的提高而增大.由图3可以看出：初始撞击速度变化情况下，框架梁结构中混凝土中的塑性变形区位置基本相同，分别在框架梁跨中、框架梁两端顶部、框架柱顶外侧和柱脚内侧.初始撞击速度提高时，框架梁的塑性区域明显扩大，而框架柱的塑性区扩大不明显.根据时程计算结果[15]还能发现，结构各部位塑性区出现的顺序依次为框架梁受撞击处、梁端顶部、梁柱节点、柱顶外侧和柱底内侧.

就雌虫而言，GST在翅膀中的表达量显著低于其他部位，而触角和残体中的表达量基本相当，分别是翅膀表达量的1.99倍和2.20倍。就雄虫而言，GST在残体中的表达水平显著低于其他部位，触角与翅膀中的表达水平基本相当，分别是残体中表达量的1.43倍和1.53倍。

由表2给出的结构内能分布情况发现，初始撞击速度V0提高时，结构及其构件的内能值基本上是增大的，但结构的总内能EI与初始撞击能量EK的比值变化很小(基本维持在91%左右)，而框架梁的内能EIb及其塑性能EPb与初始撞击能量EK的比值增大，框架柱内能EIc及其塑性能EPc和梁柱节点内能EIn及其塑性能EPn与初始撞击能量EK的比值则有所减小.

表2　结构的能量计算结果

2.2梁柱线刚度比对结构响应的影响

考虑初始撞击速度V0=3.0 m/s，初始撞击能量EK=1 800 J，框架梁柱线刚度比变化时结构的非线性冲击响应.假设框架梁宽度b=200 mm保持不变，高度h分别为400、450、500、550和600 mm，对应的梁柱线刚度比ib/ic分别为0.375、0.534、0.732、0.975、1.266.

图4给出了梁柱线刚度比变化情况下框架梁跨中挠度的时程曲线.由该图可以看出：框架梁最大挠度Umax和最终挠度Ur基本是随着梁柱线刚度比ib/ic的增大而减小的，但最大挠度出现的时间Tu比较接近，均为11 ms左右.梁柱线刚度比ib/ic从0.375增加到1.266时，框架梁的最大挠度Umax及最终挠度Ur均逐渐减小,而最终挠度与最大挠度的比值Ur/Umax在48.62%～51.96%之间波动.

表3为梁柱线刚度比变化情况下框架结构的部分响应计算结果.由表3可以看出：梁柱线刚度比的增大对结构的内能EI影响很小，90%左右的初始撞击能量被转变成为结构的内能.框架梁和框架柱的内能分别为初始撞击能量EK的73%和14%左右，框架梁和框架柱塑性变形所消耗的能量分别为初始撞击能量EK的50%和8%左右，对梁柱线刚度比的增大并不敏感.

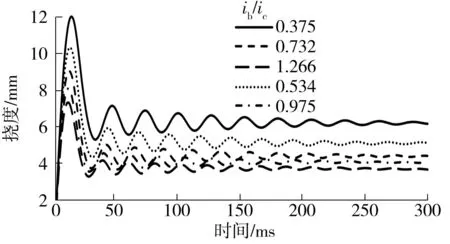
图4　框架梁跨中挠度时程曲线

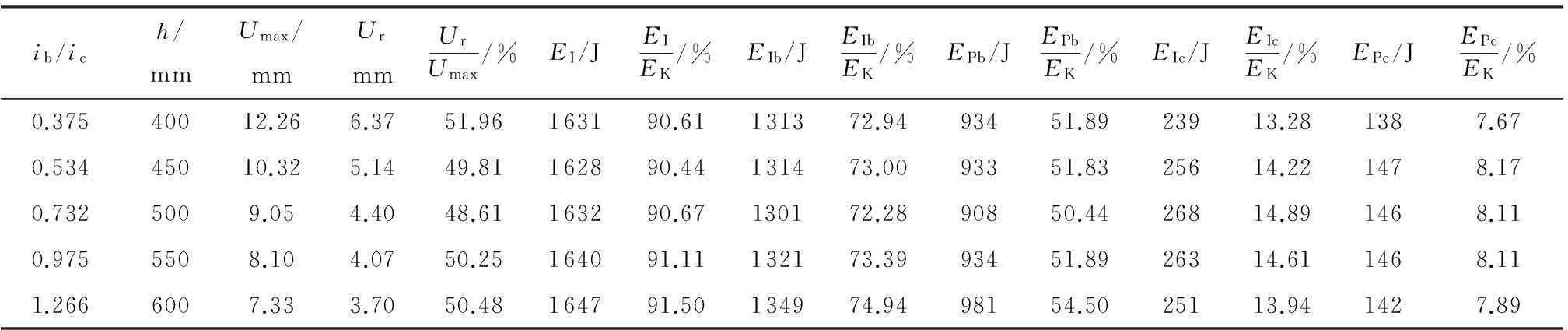
表3　不同ib/ic下的结构响应计算结果(V0=3.0 m/s)

3简化分析模型

通过对结构位移响应、塑性变形区和能量消耗情况的分析可以发现，集中对称冲击下框架梁两端及跨中混凝土开裂钢筋屈服，形成塑性变形区，因此框架梁是主要的耗能构件，而且初始撞击速度越高，结构的变形越集中于框架梁.因此文中忽略框架柱的塑性变形，假设框架梁的塑性变形模式与两端固支梁的极限状态相似[9]，则框架梁端部的塑性转角θ、塑性耗能量EPb及其动态塑性弯矩Md之间的关系为

EPb=4Mdθ

(1)

而框架梁端的塑性转角θ与跨中最终挠度Ur及结构跨度L的几何关系为

(2)假定塑性耗能EPb与初始撞击动能EK、动态塑性弯矩Md与静力受弯承载力[6]M0之间存在以下比例关系：

EPb=αEK

(3)

Md=βM0

(4)

式中,α和β为待定因子.

由非线性撞击响应分析得到的EPb、Ur计算结果，以及式(1)-(4)可以得到不同初始撞击速度和梁柱线刚度比情况下的α和β值，如表4所示.

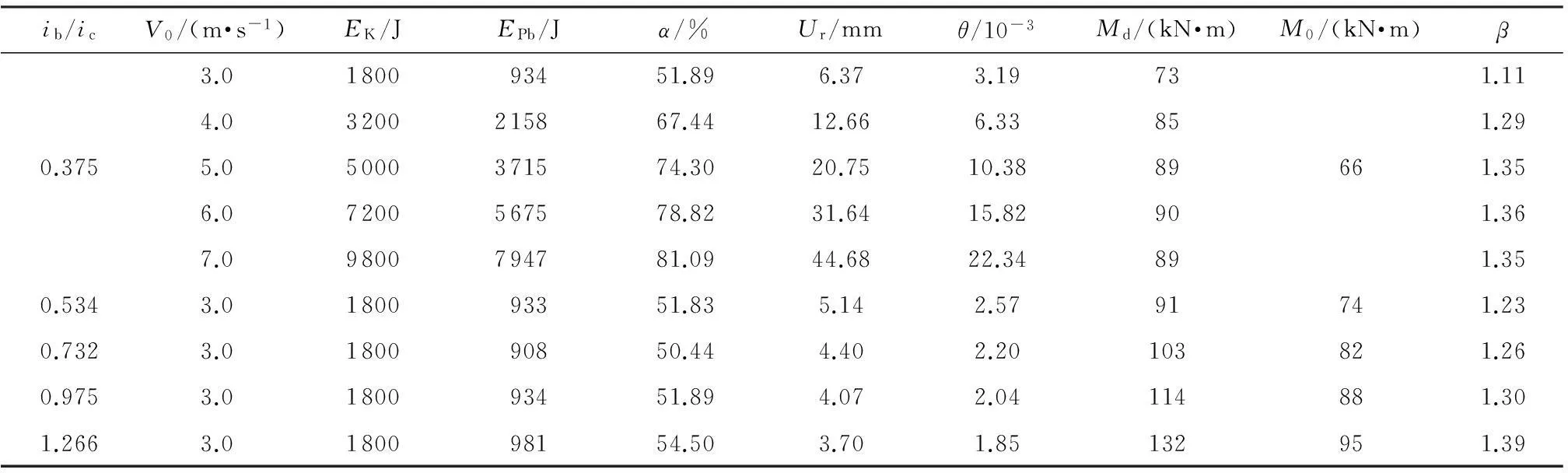
表4　α和β计算结果

由表4可以看出，随着初始撞击速度的提高，α值呈单调增大的趋势，而梁柱线刚度比的变化对α的影响不大，初始撞击速度与梁柱线刚度比均对β的值有明显影响，因此可忽略梁柱线刚度比对α的影响.通过数据拟合得出α与无量纲初始撞击速度V0/3.0之间的函数关系式：

α=1.000 0-1.007 5e-0.783 9(V0/3.0)

(5)

引入两个相互独立的修正系数C1(V0)、C2(ib/ic)，假设

β=C1C2

(6)

并利用表5中β的计算结果，通过数据拟合可以得到修正系数C1(V0)和C2(ib/ic)的函数关系式：

C1=1.220 0-15.767 7e-4.268 4(V0/3.0)

(7)

(8)

选取另外两种初始撞击速度，进行有限元分析与简化模型分析结果的对比验证.情况①：h=450 mm，ib/ic=0.534，V0=6.5 m/s；情况②：h=550 mm，ib/ic=0.975，V0=3.5 m/s.对比结果如表5所示.由表5发现：简化分析模型所得框架梁跨中最终挠度Ur1与有限元计算结果Ur2二者误差未超过5%，用简化分析得到的框架梁跨中最终挠度值控制结构设计是偏于安全的.因此，文中提出的简化分析模型及相关计算公式可以应用于实际框架结构受撞击处最终变形的估算.

表5　最终挠度计算结果对比

4结语

文中对钢筋混凝土门式框架结构在集中对称撞击下的非线性动力响应进行了有限分析，在此基础上提出了最终变形的简化分析模型和相关计算公式.通过对计算结果的分析发现：相对于梁柱线刚度比，初始撞击速度对结构撞击响应的影响较大，框架结构的塑性变形主要集中在框架梁两端及跨中，且框架梁的塑性变形随着初始撞击速度的提高明显增大，框架柱有对称向外的水平位移，柱脚内侧比柱顶后出现塑性变形区，塑性变形值也相对较小.文中提出的简化分析模型可以用于集中对称撞击下框架结构受撞击处最终位移的估算.

文中研究的撞击问题属于低速撞击，在高速撞击下混凝土的非线性本构关系以及撞击过程中的局部热应力等问题是需要进一步研究的课题.

参考文献：

[1]陆新征，江见鲸．世界贸易中心飞机撞击后倒塌过程的仿真分析 [J]．土木工程学报，2001，34(6)：8- 10．

LU Xin-zheng，JIANG Jian-jing．Dynamic finite element similation for the collapse of World Trade Center [J]．China Civil Engineering Journal，2001，34(6)：8- 10.

[2]许清风，王孔藩，李向民．世界贸易中心倒塌原因浅析 [J]．钢结构，2002，17(3)：54- 56．

XU Qing-feng，WANG Kong-fan，LI Xiang-min．Bried analysis on the causes of the collapse of World Trade Center [J]．Steel Construction，2002，17(3)：54- 56．

[3]夏超逸，张楠，夏禾．汽车撞击作用下车桥系统的动力响应及高速列车运行安全分析 [J]．工程力学，2013，30(8)：119- 126.

XIA Chao-yi，ZHANG Nan，XIA He．Dynamic response of train-bridge system subjected to truck collision and running safety evaluation of high-speed train [J]．Engineering Mechanic，2013，30(8)：119- 126．

[4]肖波，周楚兵，吴卫国,等．船与刚性桥墩的碰撞性能分析 [J]．武汉理工大学学报(交通科学与工程版) ，2005，29(6)：855- 857.

XIAO Bo，ZHOU Chu-bing，WU Wei-guo，et al．Analysis on collision characteristic of ship and rigid pier [J]．Journal of Wuhan University of Technology(Transportation Science and Engineering)，2005，29(6)：855- 857．

[5]熊安平，胡本清，杜宜洋．用LS-DYNA仿真模拟探索船舶刚度对船桥撞击力的影响 [J]．高速铁路技术，2012，3(1)：24- 26,72.

XIONG An-ping，HU Ben-qing，DU Yi-yang．Discussion of impact force in vessel-pier crash influenced by ship stiffness with LS-DYNA simulation [J]．High Speed Railway Technology，2012，3(1)：24- 26,72．

[6]张瑞坤，王兴国，葛楠．侧向撞击作用下钢筋混凝土柱动力响应的有限元分析 [J]．工程抗震与加固改造，2010，32(1)：30- 33．

ZHANG Rui-kun，WANG Xing-guo，GE Nan．Finite element analysis of the dynamic responses of RC column under lateral impact [J]．Earthquake Resistant Engineering and Retrofitting，2010，32(1)：30- 33．

[7]刘廷权，王兴国，葛楠．钢筋混凝土柱在侧向撞击作用下破坏模式研究 [J]．武汉理工大学学报，2010，32(9)：188- 193．

LIU Ting-quan,WANG Xin-guo,GE Nan．Investigation into failure mode of RC column subjected to impulsive load [J]．Journal of Wuhan University of Technology，2010，32(9)：188- 193．

[8]王兴国，苏幼坡，葛楠．侧向撞击作用下钢筋混凝土框架柱简化模型研究 [J]．广西大学学报(自然科学版)，2011，36(1)：15- 20．

WANG Xing-guo，SU You-po，GE Nan．Research on a simplifeied reinforced concrete frame column model subjected to lateral impact [J]．Journal of Guangxi University(Natural Science Edition)，2011，36(1)：15- 20．

[9]刘锋，吕西林．冲击载荷作用下框架结构的非线性动力响应 [J]．振动工程学报，2008，21(2)：107- 114．

LIU Feng,LÜ Xi-lin.Nonlinear dynamic responses of impulsive loaded frame structures [J].Journal of Vibration of Engineering，2008，21(2)：107- 114．

[10]于敏．混凝土框架结构的落层倒塌碰撞分析 [D]．广州：华南理工大学土木与交通学院，2012．

[11]高菲．高速撞击下钢筋混凝土立体框架力学响应的数值模拟 [D]．重庆：西南科技大学土木工程与建设学院，2013．

[12]魏德敏，刘德源．钢筋混凝土梁冲击响应及其影响因素分析 [J]．北京理工大学学报，2014，34(S1)：119- 122．WEI De-min,LIU De-yuan.Analysis of impact response of RC beams and influencing factors [J].Transactions of Beijing Institute of Technology，2014，34(S1)：119- 122．

[13]GB50010—2010，混凝土结构设计规范 [S].

[14]王政．弹靶侵彻动态响应的理论与数值分析 [D]．上海：复旦大学力学与工程科学系，2005．

[15]刘德源．钢筋混凝土结构撞击响应分析 [D]．广州：华南理工大学土木与交通学院，2014．

Nonlinear Response of Reinforced Concrete Frame Structures Under Symmetrical Impact

WEIDe-min1,2LIUDe-yuan1LIDi1

(1. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640,Guangdong, China;2. State Key Laboratory of Subtropical Building Science,South China University of Technology,Guangzhou 510640,Guangdong,China)

Abstract:Dealt with in this paper is the nonlinear dynamic response of reinforced concrete frame structures under symmetrical centralized impacts. In the investigation,first,two influencing factors, namely the initial impact velocity of the drop hammer and the beam-to-column linear stiffness ratio,are analyzed.Next,a nonlinear finite element analysis is performed to explore the variations of the impact force with time,the displacement response of the structure, the final deformation,the characteristics of the plastic deformation and the energy consumption of the structure.Then,the computational results are analyzed and a simplified model to estimate the final deformation of the impact point is put forward. Finally,a comparison is made between the results respectively obtained by the finite-element computation and the simplified model. It is found that(1) the influence of initial impact velocity on the structure's dynamic response is more evident than that of the beam-to-column linear stiffness ratio;(2) the plastic deformation of the frame structure mainly occurs at the two ends and in the midpoint of the beam, which greatly increases with the increase of the initial impact velocity;and(3) the horizontal displacement of the two frame columns is symmetrically outward and the plastic deformation of the column is relatively smaller than that of the beam.

Key words:reinforced concrete frame structure;symmetrical impact;initial impact velocity;linear stiffness ratio;nonlinear dynamic response;finite element analysis

doi：10.3969/j.issn.1000-565X.2016.02.002

中图分类号：TU 375.1

文章编号:1000- 565X(2016)02- 0008- 06

作者简介:魏德敏(1955-),女,教授,博士生导师,主要从事土木工程结构防灾减灾研究.E-mail:dmwei@scut.edu.cn

*基金项目:国家自然科学基金资助项目(51025829)

收稿日期:2015- 03- 06

Foundation item: Supported by the National Nutural Science Foundation of China(51025829)