春季纵连板式无砟轨道非线性温度分布*

戴公连　苏海霆　闫斌　朱俊檏

(中南大学 土木工程学院， 湖南 长沙 410075)



春季纵连板式无砟轨道非线性温度分布*

戴公连苏海霆†闫斌朱俊檏

(中南大学 土木工程学院， 湖南 长沙 410075)

摘要：为得到圆曲线上无砟轨道结构温度场分布的时变规律，在某客运专线圆曲线段上的CRTSⅡ型纵连板式无砟轨道中埋设温度传感器，对其温度分布进行了长期连续观测，在大量测试数据的基础上通过概率统计获得无砟轨道横、竖向温度梯度荷载模式.结果表明：无砟轨道结构在与外界的热交换过程中，其内部竖向和横向温度呈非线性分布；轨道结构温度随着环境温度变化呈现周期性变化；随着与表面距离的增加，不同位置处出现温度峰值的时间存在明显滞后，轨道结构底部出现温度峰值的时间比顶部延迟约5 h；无砟轨道竖向温度梯度分布曲线符合指数分布规律，与中国铁路设计规范规定的箱梁竖向温度梯度分布曲线在形式上较为相近.

关键词：铁路桥梁；轨道工程；无砟轨道；非线性温度；试验研究

由于具有整体性好、平顺度高、工厂预制化程度高、维修少等特点[1]，CRTSⅡ型纵连板式无砟轨道已被广泛应用于我国京津、京沪、沪杭、京武、合蚌、杭甬、杭长和合福等多条高铁线路上，总铺设双线里程已超过双线4 500 km.由于混凝土材料导热性能较差[2- 5]，无砟轨道结构与外界环境的热交换过程中其内部温度场分布极为复杂，存在着竖向和横桥向非线性温差，这是引起轨道板上鼓、表面开裂、曲线段无砟轨道横向变形的主要诱因[6- 9].

关于纵连板式无砟轨道竖向温度分布规律，既有研究中多通过对施工过程中轨道结构几天温度变化的测试来假设温度梯度，再通过有限元模拟计算受力特征，且研究对象多局限于轨道板,并不考虑底座板温度变化的影响[10- 13].而对设置超高后无砟轨道横向温度模式的研究仍较为匮乏.

笔者已对秋季无砟轨道温度场做了较为详细的分析[14- 15]，为研究春季(3月至5月)曲线段轨道板和底座板中的温度分布情况，文中对某客运专线圆曲线上CRTSⅡ板式无砟轨道温度场进行了长期监测，研究其竖向和横向温度分布的时变规律，通过对春季测试数据的统计拟合提出适用于我国典型地区无砟轨道的竖向和横向温度梯度模式.

1圆曲线段无砟轨道温度场测试

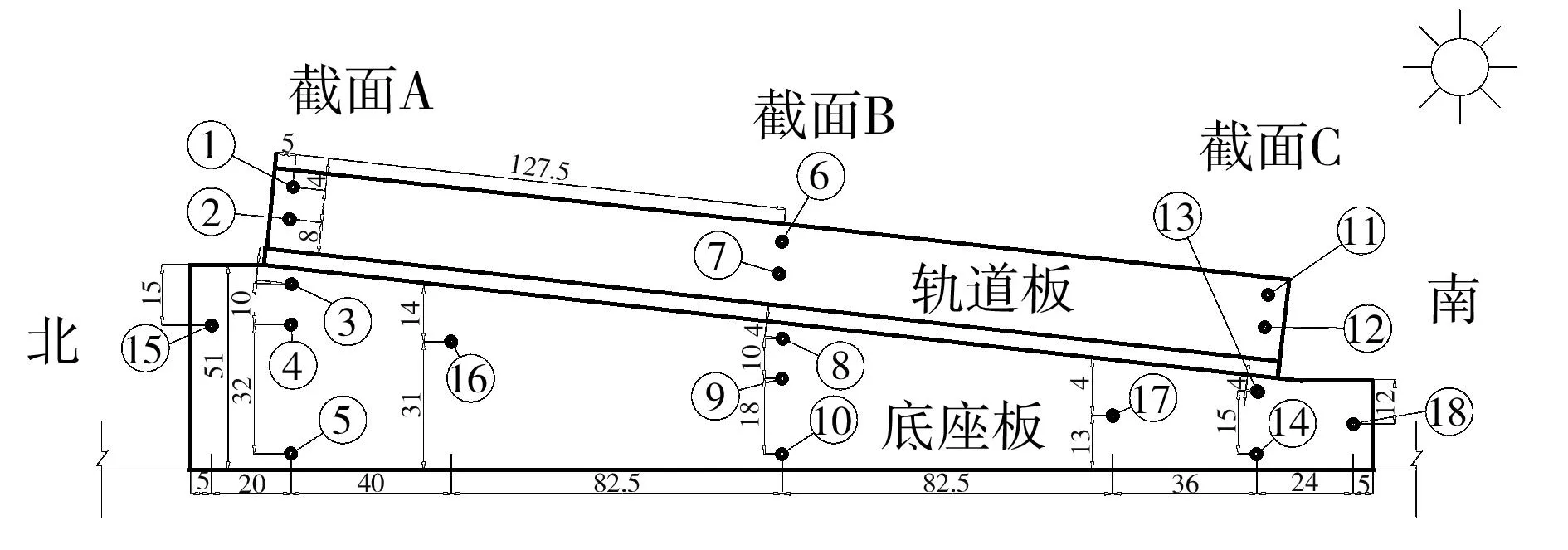
图1　轨道板底座板测点布置示意图(单位：cm)

Fig.1Schematic diagram of measuring point layout of track board base plate(Unit:cm)

测试时间为2014年3月至5月，截面A的实测数据见图2.

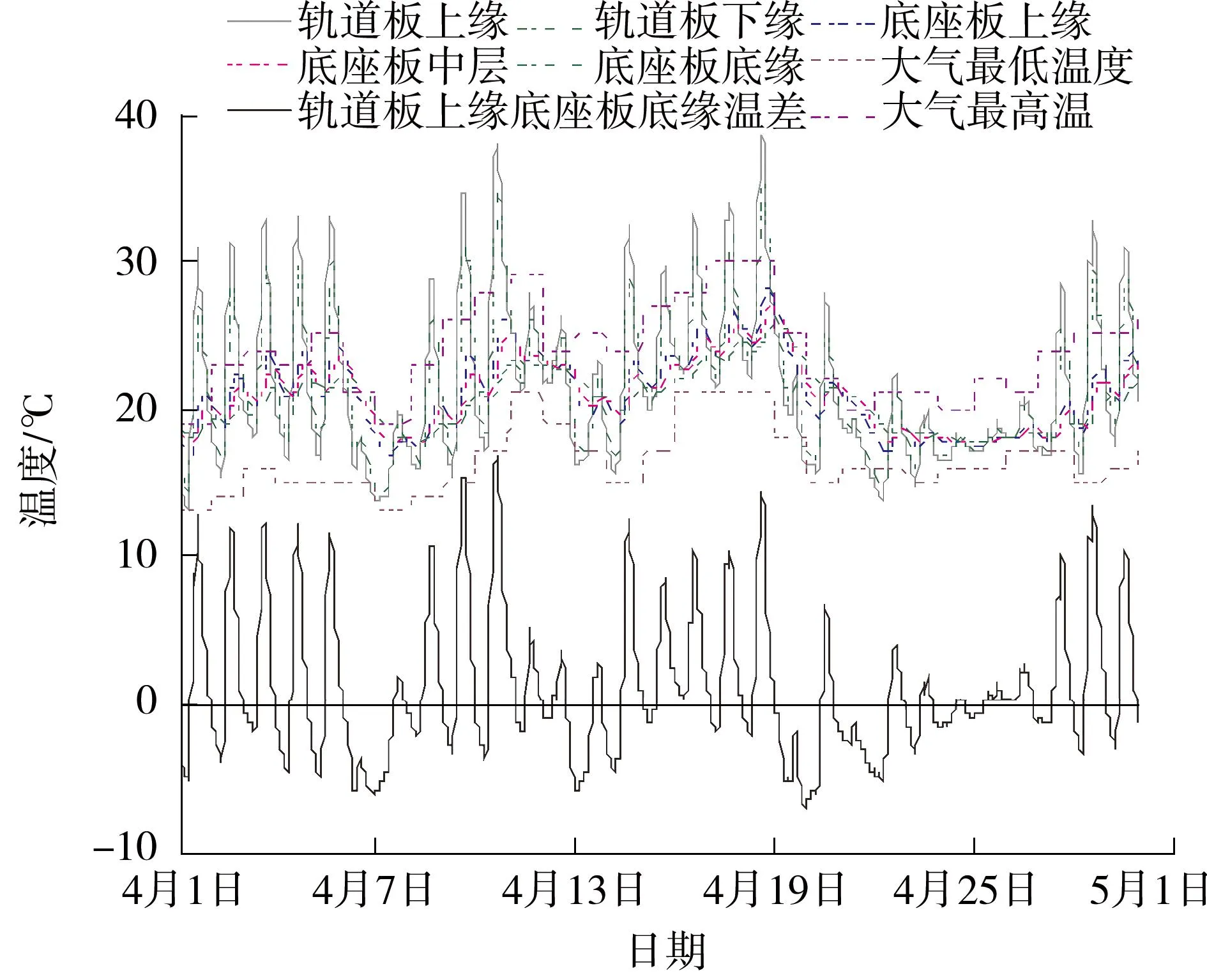
图2　无砟轨道截面A测点实测温度

轨道结构各截面具有相似的规律，均具有典型的周期日变化特性，分析结果如表1所示.

表1无砟轨道日变化规律统计表1)

Table 1Statistic rules of daily temperature change in ballstless track

位置tlΔtl/℃thΔth/℃Δt/℃Δtmax/℃轨道板顶部7:30-0.3～3.415:0011.4～14.223.424.6轨道板底部7:301.0～4.616:308.1～10.818.820.2底座板顶部6:304.0～7.717:301.3～3.79.19.7底座板底部8:004.3～8.619:30-1.0～0.96.06.5

将春季轨道结构中出现最大温度值时刻4月10日15:00(当天天气晴转多云，17～28 ℃)和轨道结构中出现最低温度值时刻3月9日7:30(当天天气阴转多云，4～14 ℃)，以所有测点温度为基准在轨道结构范围内进行拟合并适当外延，可得到轨道板与底座板等温线分布云图.

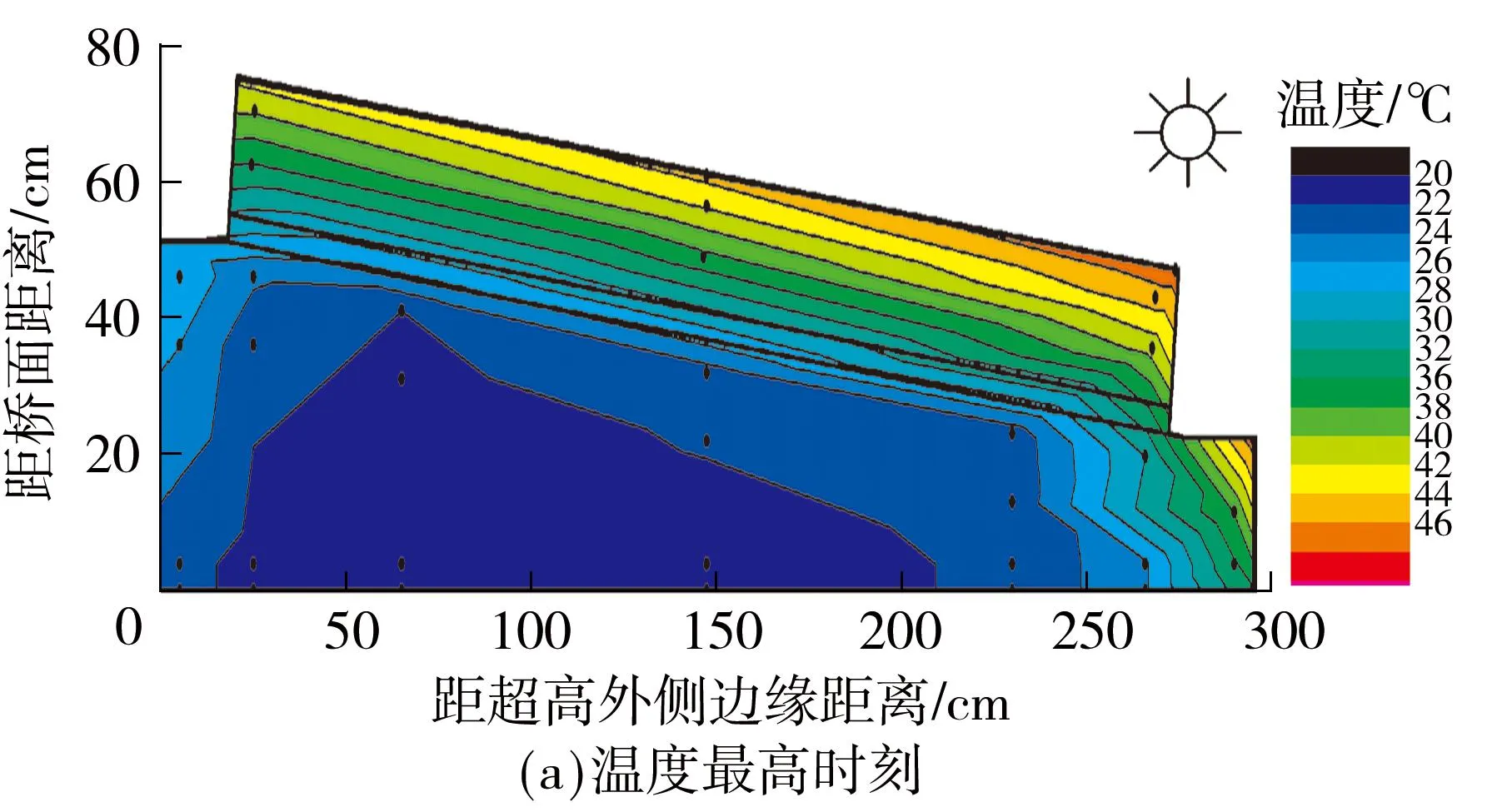
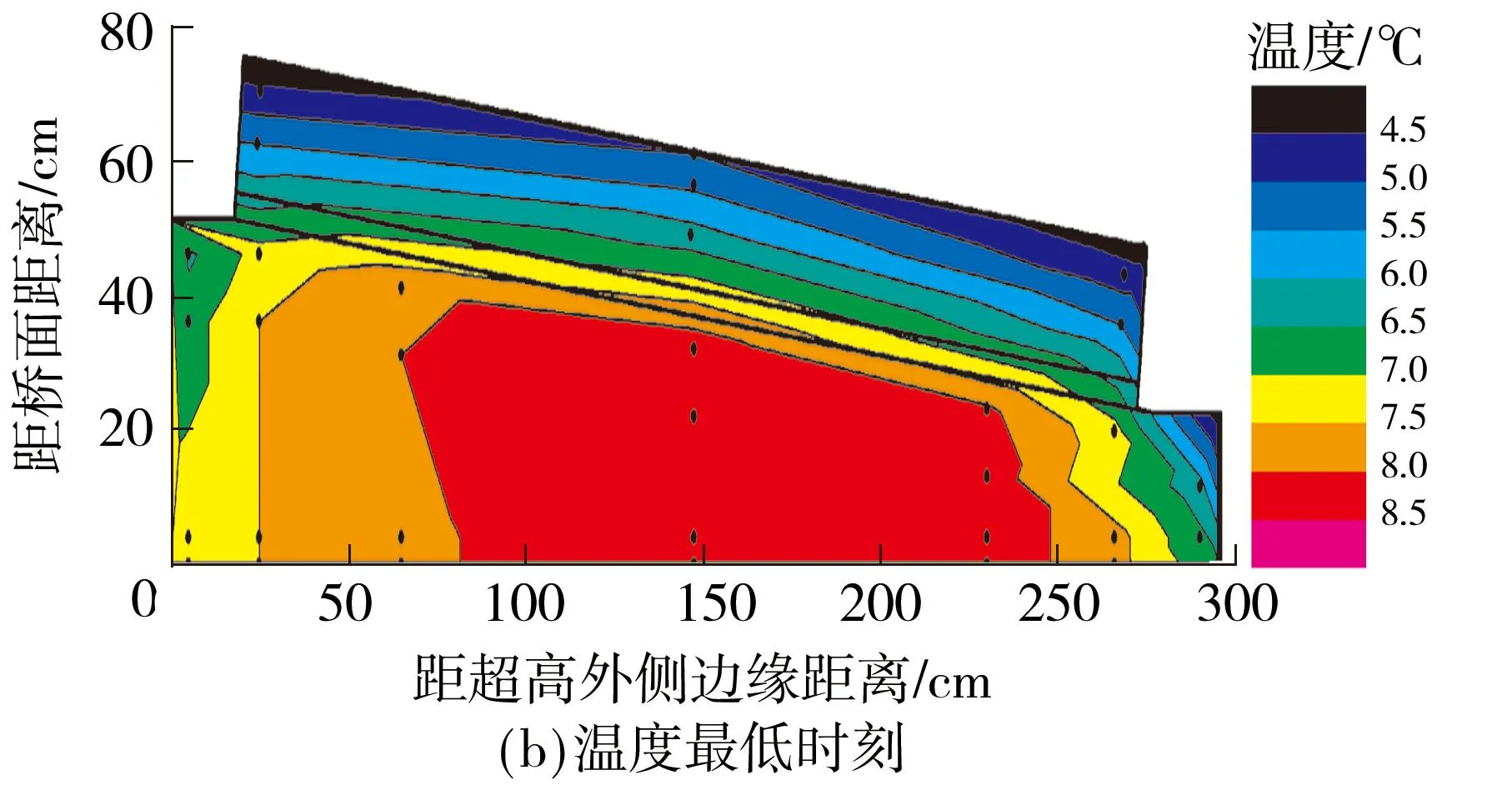
图3　轨道结构最值温度时刻等温线云图

Fig.3Isotherm figures of the most value time in ballstless track structure

由图3可以看出，轨道板中的等温线分布密集，底座板分布较稀疏，说明轨道板受外界环境影响大，存在较大的温度梯度，底座板因受轨道板的遮盖，使温度变化较为缓和.由于混凝土导热系数较小，导致整个轨道结构的温度场分布情况与外表面温度相比出现明显延迟，因此轨道结构竖向和横向存在非线性温度梯度.

2无砟轨道竖向温度梯度分布规律

2.1竖向温度梯度日变化规律

以4月10日为例，将截面B竖向温度梯度随时间的变化情况绘于图4中.

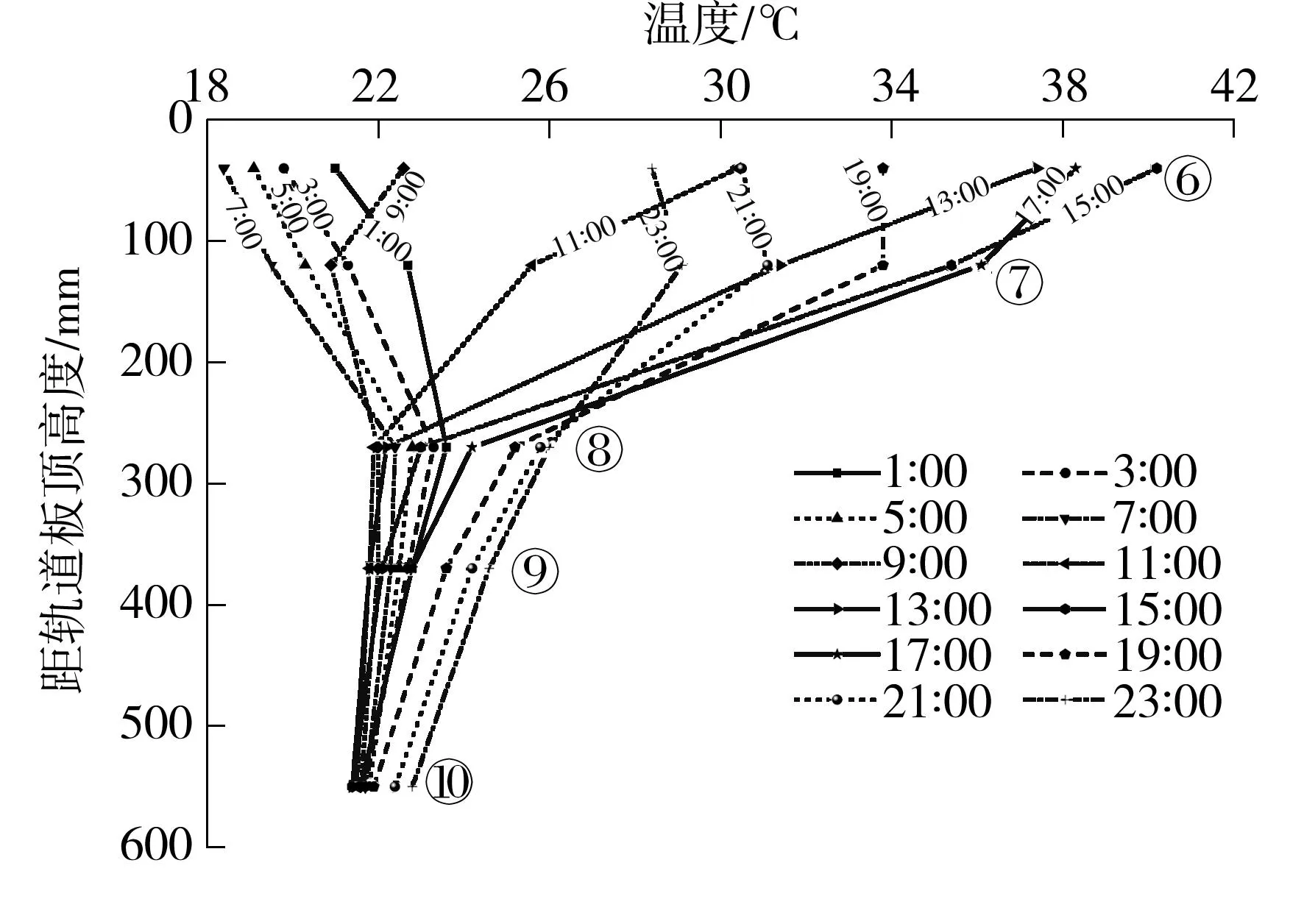
图4　截面B竖向温度梯度日变化规律

Fig.4Daily distribution of vertical temperature gradient in section B

由竖向梯度每天的变化分布分析可知，无砟轨道竖向温度梯度分布主要有3种模式，一般从夜晚23:00之后至第2天的8:00左右为负梯度模式，9:00左右出现顶部与底部温度相同的模式，自9:00至23:00在轨道结构中基本以正温度梯度为主.对于整个轨道结构来说超过300 mm后日温度变化较小.

2.2日最大竖向温度梯度分布

从文中监测到的数据分析(2014年3月至5月)，最大的竖向正负温度梯度分布如图5所示.

轨道板结构春季中竖向最大正温差出现在4月10日15:00.天气晴，气温17～28 ℃，太阳辐射强烈，日出后1 h内轨道结构上表面温度开始上升，在强烈的太阳辐射下升温较快，并于15:00达到峰值温度(40.5 ℃)，因混凝土导热性较差，引起轨道结构下表面温度上升较慢，至夜晚23：00达到最大温度值(24 ℃)，轨道结构上表面与下表面出现峰值的时间相差近8 h，期间自上午9:00开始出现正温差，差值不断增加，最大温差出现在15:00(约为18 ℃)，之后差值不断减小，至晚间23:00轨道结构温差趋于一致；之后轨道结构内出现负温差，并于早上6:30左右达到系统最大负温差，轨道结构春季竖向最大负温差出现在3月21日(最大负温差约为8 ℃)，之后负温差开始减小，并在早上8:30上下表面趋于一致.

2.3竖向平均温度梯度分布

江西南昌春季(3月、4月、5月)多雨，其中晴天共计5 d，多云或阴天共计34 d，雨天共计53 d，取每天各温度模式最大值进行平均得到各模式平均温度梯度，各截面的平均温度梯度分布如图6所示，对于晴天状况下的竖向正温度梯度，截面A的平均值为21.01 ℃/m，截面B的平均值为29.09 ℃/m，截面C的平均值为36.30 ℃/m；对于晴天状况下的竖向负温度梯度，截面A的平均值为7.25 ℃/m，截面B的平均值为9.45 ℃/m，截面C的平均值为11.01 ℃/m.

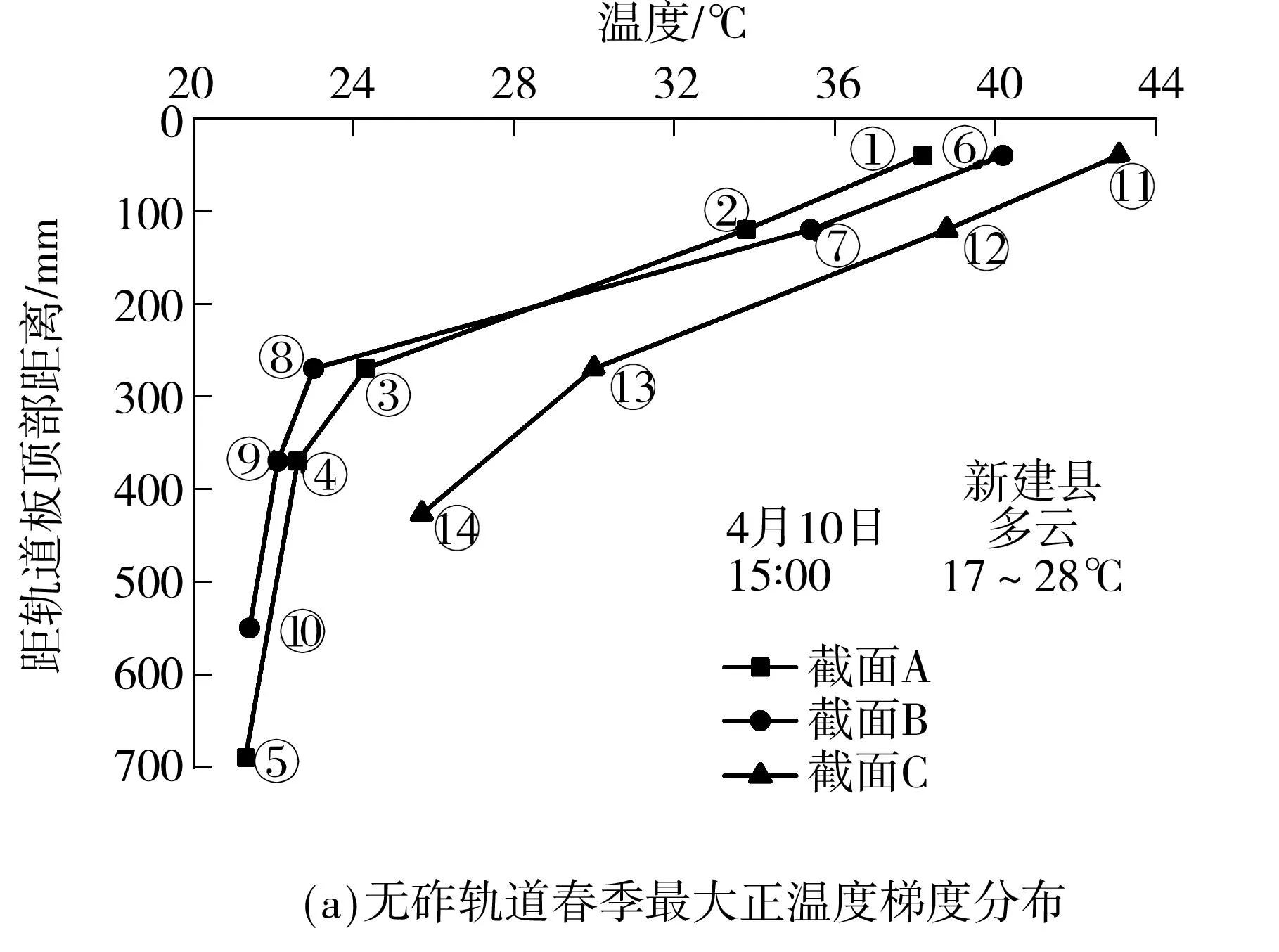
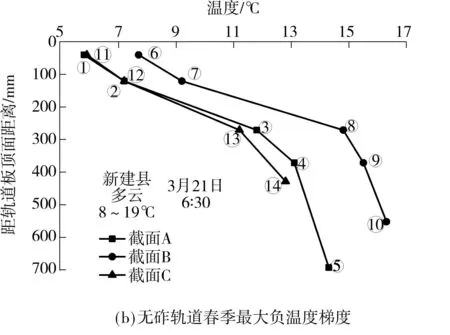
图5　各截面最大温度梯度分布

Fig.5Distribution of maximum temperature gradient in each section

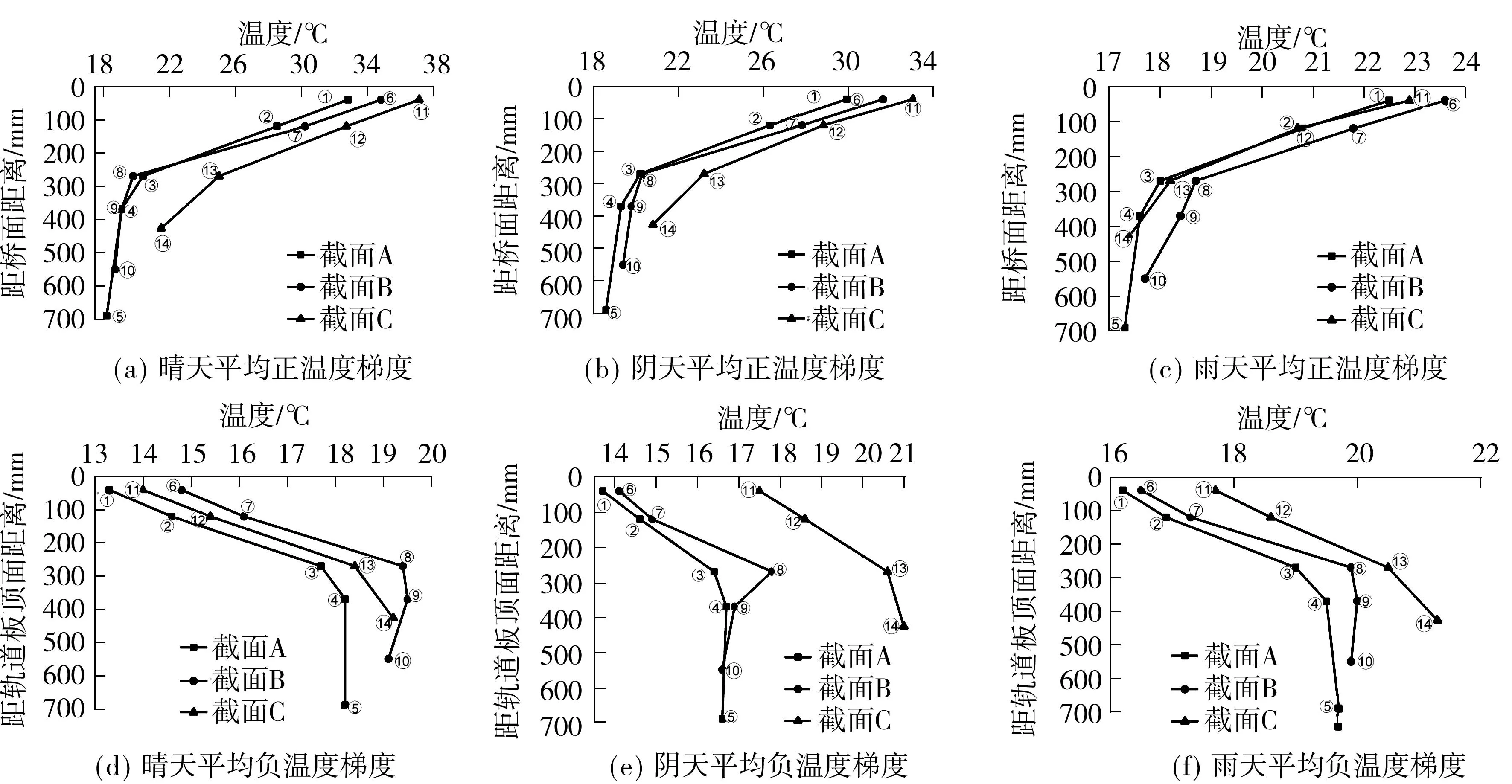
图6　各截面竖向温度梯度平均分布

3无砟轨道横向温度梯度分布规律

3.1横向温度梯度日变化规律

底座板上表面中部受轨道板遮挡，而两侧未受遮盖，从而导致轨道板与底座板的横向温度分布规律不同，应予以分别研究.取轨道板底层与底座板中间距离顶面相同距离点的4月10日温度数据绘制日变化规律图，如图7所示.

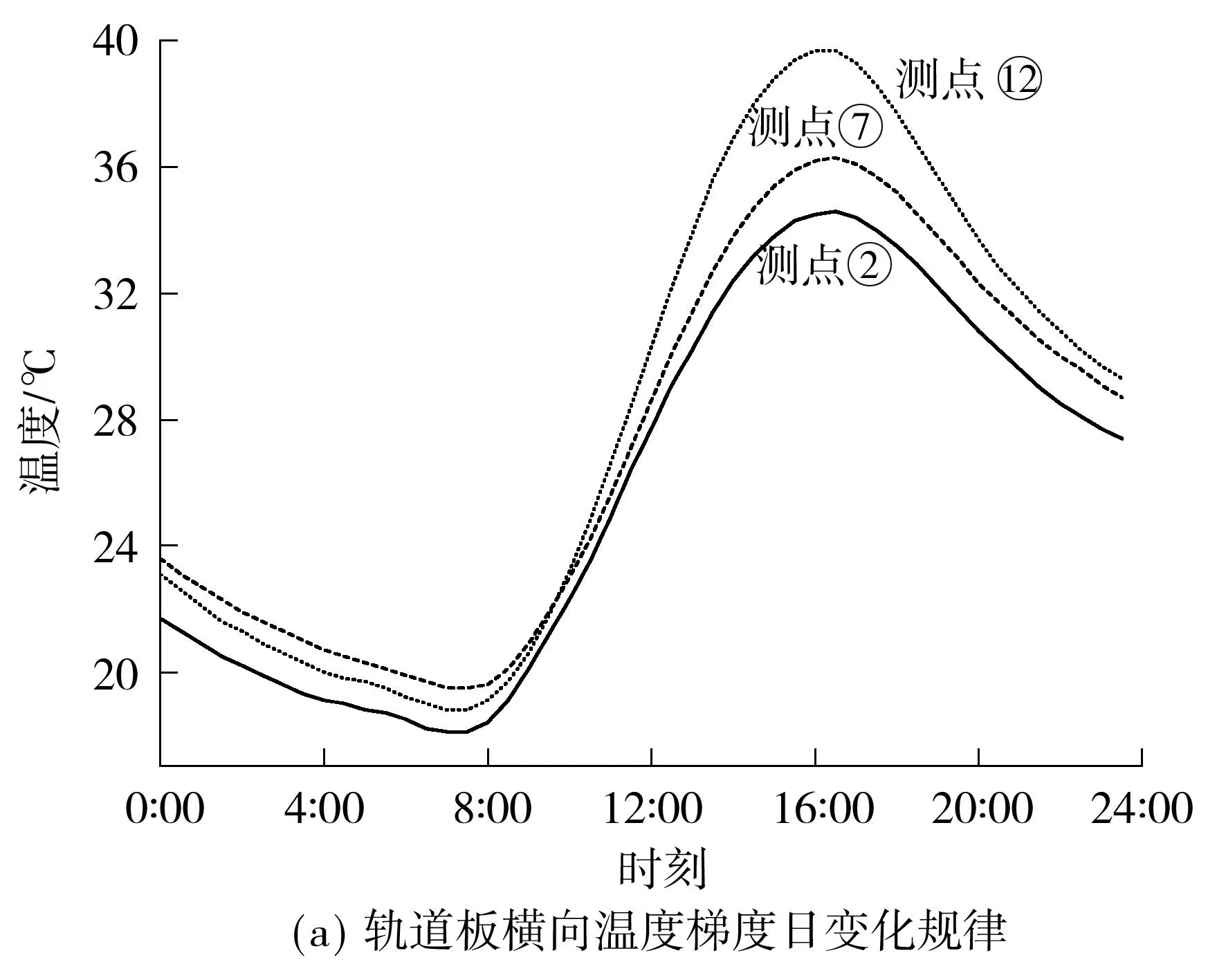
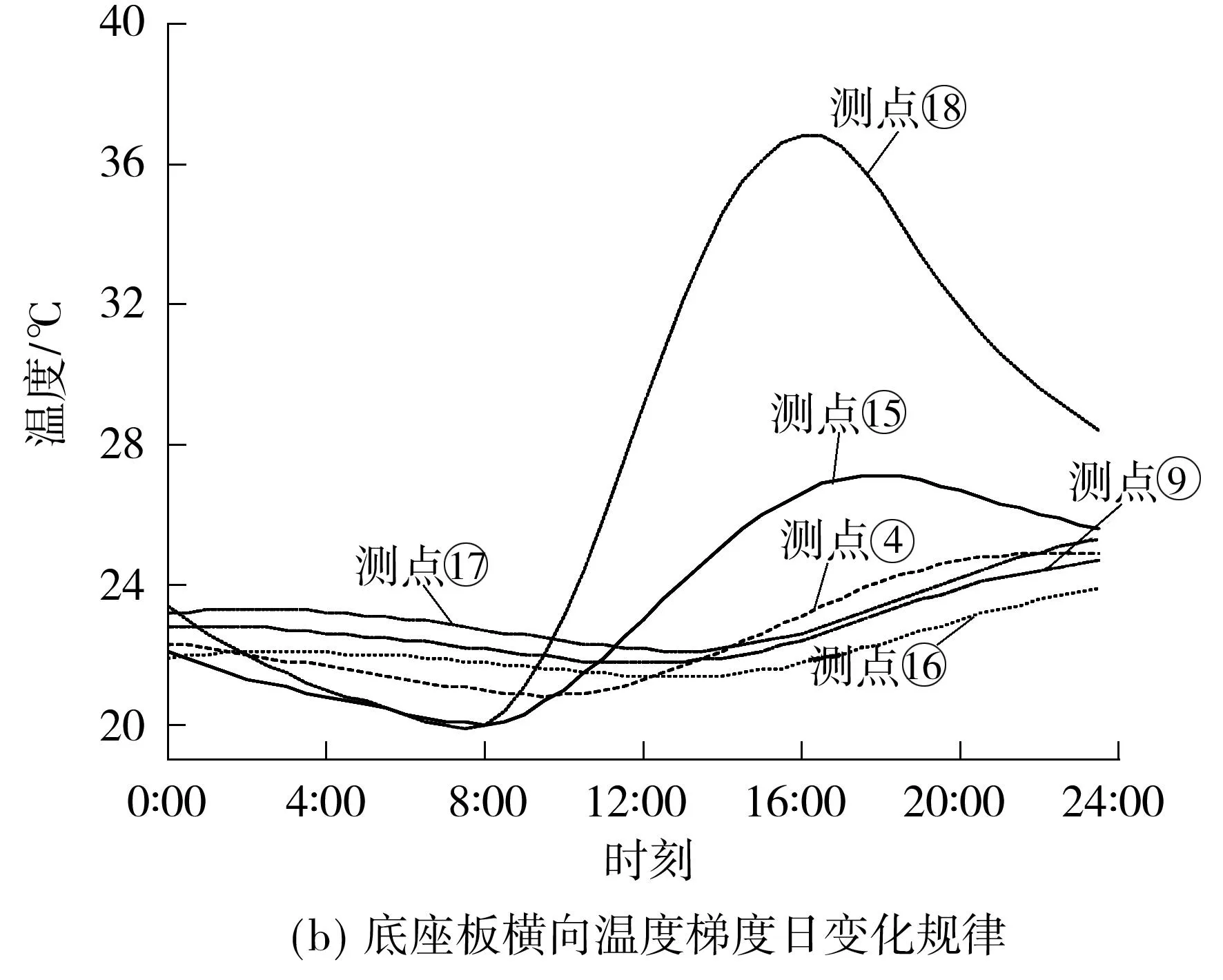
图7　轨道板与底座板横向温度日变化规律

Fig.7Daily distribution of horizontal temperature in track slab and base plate

因轨道板只遮盖底座板的中部，两侧可以受到阳光直射，所以底座板中间部分与外侧部分温度差别较大，底座板中部受轨道板遮盖的区域温度变化平缓，相差在2 ℃以内；底座板北侧温度较中部受遮盖部分相差可达13 ℃.所以宜将底座板温度模式分为3种.其中模式1为底座板北侧温度较中部高，通常南侧的温度也较中间高，整体温度分布呈现U形；模式2为底座板北侧温度较中间低，通常此时南侧的温度也较中间低，整体温度分布呈现倒U形，模式3为各测点温度较为一致，成一条直线.

3.2横向平均温度梯度分布

统计春季晴天状况下轨道板和底座板横向梯度的平均温度分布如图8所示.在春季晴天中并未出现轨道板的模式2形式，在多云和雨天气候中出现，在各模式中尤以底座板的模式1的梯度最大.

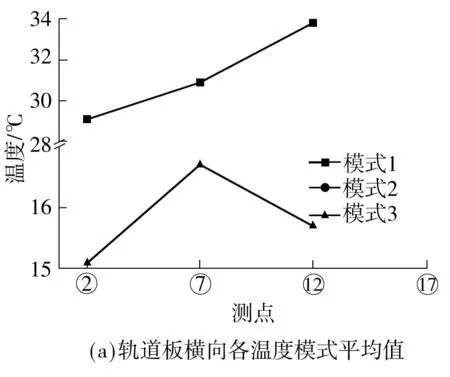
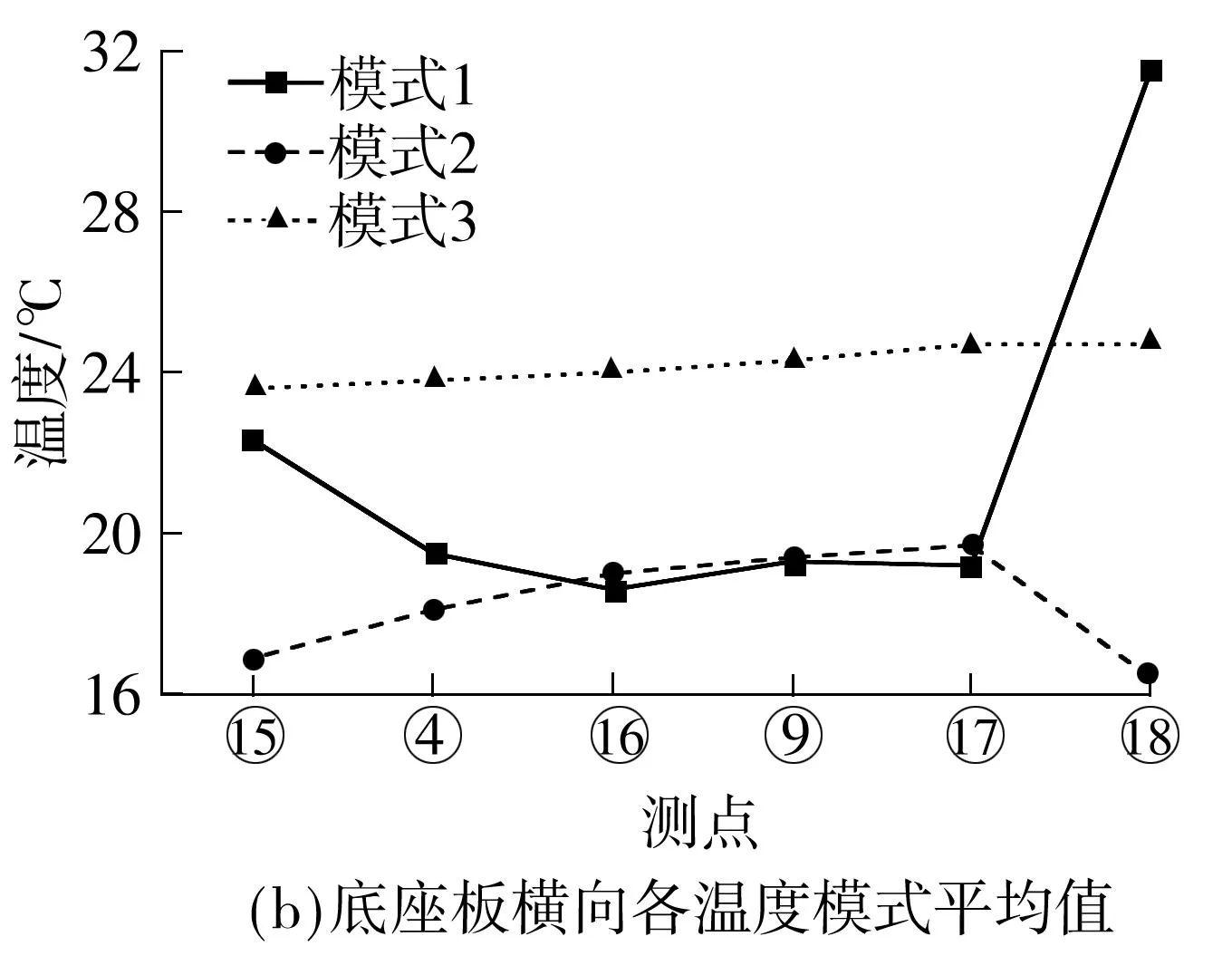
图8　无砟轨道横向温度梯度晴天平均分布

Fig.8Average horizontal temperature gradient in sunny weather

4曲线段无砟轨道温度荷载模式

4.1竖向温度荷载模式

通过对数据的整理和拟合，无砟轨道竖向温度梯度分布拟合曲线如图9所示，因截面C侧面也能够接收阳光辐射，所以正温度梯度中采用截面A和截面B温度值的平均拟合为第一条曲线，采用截面C的温度值单独拟合为一条曲线，负温度梯度中采用3个截面的温度平均值拟合成一条曲线，对测试时间内晴天平均梯度进行回归拟合，得到典型地区竖向温度梯度荷载模式.

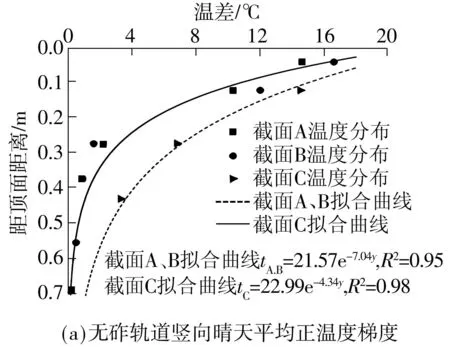
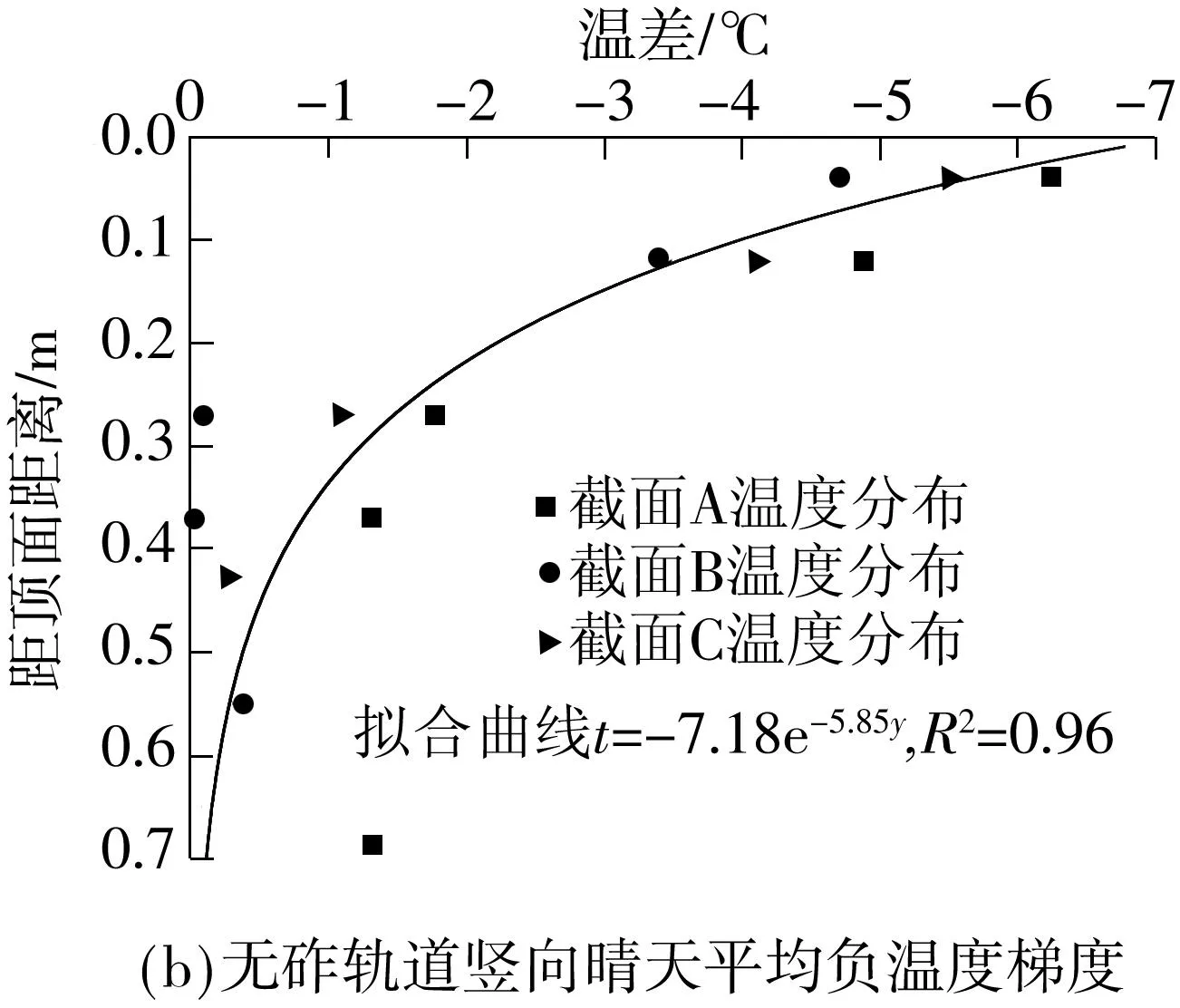
图9　无砟轨道竖向温度梯度晴天拟合曲线

Fig.9Fitting curves of vertical temperature gradient in sunny weather

竖向温度梯度晴天平均正温度梯度曲线为

tA,B=21.57e-7.04y

(1)

tC=22.99e-4.34y

(2)

式中：tA,B为对截面A、B拟合的温度分布，℃；tC为对截面C拟合的温度分布，℃；y为距顶面距离，m.

竖向温度梯度晴天平均负温度梯度曲线将3条曲线平均为一条后拟合为

t=-7.18e-5.85y

(3)

式中，t为分别对截面A、B、C数据平均后拟合的温度分布，℃.

拟合结果中相关系数的平方均在0.9以上，说明拟合结果较为可靠.

以上竖向拟合数据与中国铁路桥梁设计规范中箱梁竖向温度梯度分布[16](指数分布)在形式上吻合较好.

4.2横向温度荷载模式

对测试时间内轨道板和底座板横向晴天平均温度梯度分布分别进行回归拟合，得到典型地区横向温度梯度荷载模式.

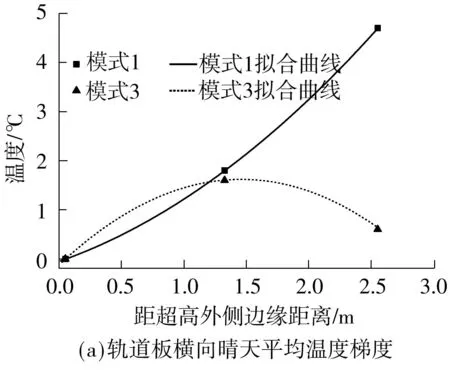
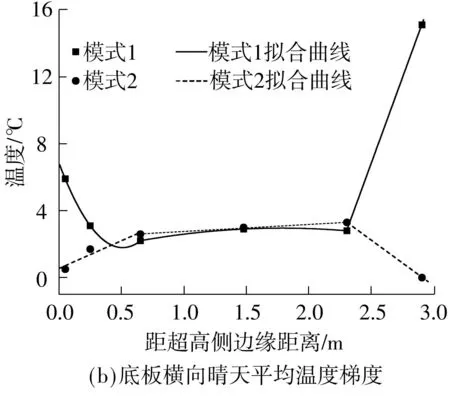
图10　无砟轨道横向温度梯度晴天拟合曲线

Fig.10Fitting curves of horizontal temperature gradient in sunny weather

轨道板横向平均温度梯度曲线可拟合为如下形式.

模式1：

t1=0.38x2+0.89x-0.05

(4)

模式3：

t3=0.82x2+2.39x-0.12

(5)

底座板横向平均温度梯度曲线可拟合如下形式.

模式1：

(6)

模式2：

(7)

式中，x为距超高侧边缘距离，m.拟合结果中相关系数的平方均在0.95以上，说明拟合结果较为可靠.

5结论

对我国中部地区高速铁路某客运专线上CRTSⅡ型纵连板式无砟轨道春季数据的观测与分析表明：

(1)无砟轨道在与外界环境热交换过程中，结构内部存在着竖向和横向非线性温度场;

(2)随着轨道结构厚度的增加，不同位置处出现温度峰值的时间存在明显滞后，春季轨道结构底部出现温度峰值的时间与顶部相差约5h;

(3)春季无砟轨道竖向温度梯度分布曲线符合指数分布规律，与中国铁路规范[16]的箱梁竖向温度梯度分布曲线在形式上较为相近；

(4)春季轨道板横向温度梯度宜采用二次函数回归拟合，底座板温度梯度宜采用三段线分别进行拟合;

(5)文中仅考察了我国中部地区高速铁路轨道设计提供温度荷载模式，是否适用于其他地区的温度荷载模式有待进一步研究.

参考文献：

[1]石现峰.高速铁路无砟轨道结构的设计理论研究 [D].北京：中国铁道科学研究院,2007.

[2]闫斌,戴公连,苏海霆.基于气象资料的轨道板竖向温度梯度预测模型 [J].华南理工大学学报(自然科学版),2014,42(12):9- 13.

YAN Bin,DAI Gong-lian,SU Hai-ting.A meteorological parameters-based prediction model of vertical temperature gradient of track plate [J].Journal of South China University of Technology(Natural Science Edition),2014,42(12):9- 13.

[3]JOHN B Kennedy,MOHAMED H Soliman.Temperature distribution in composite bridges [J].Journal of Structure Engineering,1987,113(3):475- 482.

[4]XU Y L,CHEN B,NG C L,et al.Monitoring temperature effect on a long suspension bridge [J].Structural Control & Health Monitoring，2011，17(6):632- 653.

[5]戴公连,郑鹏飞,闫斌，等.日照作用下箱梁桥上无缝线路纵向力研究 [J].浙江大学学报,2013,47(4):609- 614.DAI Gong-lian,ZHENG Peng-fei,YAN Bin,et al.Longitu-dinal force of CWR on box girder under solar radiation [J].Journal of Zhejiang University,2013,47(4):609- 614.

[6]胡所亭.高速铁路预应力混凝土箱梁竖向温度梯度效应研究 [D].北京：中国铁道科学研究院,2008.

[7]王继军,尤瑞林,王梦,等.单元板式无砟轨道结构轨道板温度翘曲变形研究 [J].中国铁道科学,2010,31 (3):9- 14.

WANG Ji-jun,YOU Rui-lin,WANG Meng,et al.Research on the slab temperature warping of the unit slab track system [J].China Railway Science,2010,31(3):9- 14.

[8]凯尔别克 F.太阳辐射对桥梁结构的影响 [M].刘兴法，译.北京：中国铁道出版社，1981:9- 46.

[9]ELBADRY M M,GHALI A.Temperature variations in concrete bridges [J].Journal of the Structural Engineering,ASCE,1983,109(10):2355- 2374.

[10]王森荣,孙立,李秋义,等.无砟轨道板温度测量与温度应力分析 [J].铁道工程学报,2009(2):52- 55.

WANG Sen-rong,SUN Li,LI Qiu-yi,et al.Temperature measurement and temperature stress analysis of ballastless track slab [J].Journal of Railway Engineering Society,2009(2):52- 55.

[11]韩志刚,孙立.CRTSⅡ型板式无砟轨道板温度测量与变形分析 [J].铁道标准设计,2011(10):41- 44.

HAN Zhi-gang,SUN Li.Temperature measurement and deformation analysis for CRTSⅡballastless track slabs [J].Railway Standard Design,2011(10):41- 44.

[12]卫军,班霞,董荣珍.温度作用对CRTSⅡ型无砟轨道结构体系的影响及损伤分析 [J].武汉理工大学学报,2012，34(10):80- 85.

WEI Jun,BAN Xia,DONG Rong-zhen.Analysis of effects and damage of CRTSⅡ ballastless track structure system induced by temperature [J].Journal of Wuhan University of Technology,2012,34(10):80- 85.

[13]刘钰,赵国堂.CRTSⅡ型板式无砟轨道结构层间早期离缝研究 [J].中国铁道科学,2013，34(4):1- 7.

LIU Yu,ZHAO Guo-tang.Analysis of early cap between layers of CRTSⅡ slab ballastless track structure [J].China Railway Science,2013，34(4):1- 7.

[14]戴公连,苏海霆,闫斌.圆曲线段无砟轨道横竖向温度梯度研究 [J].铁道工程学报,2014(9):40- 45.

DAI Gong-lian,SU Hai-ting,YAN Bin.Study on horizontal and vertical temperature gradient of ballastless track on curve line [J].Journal of Railway Engineering Society,2104(9):40- 45.

[15]戴公连,苏海霆,闫斌.秋季桥上纵连板式无砟轨道竖向温差试验研究 [J].湖南大学学报(自然科学版),2015,42(3):94- 99.

DAI Gong-lian,SU Hai-ting,YAN Bin.Experimental study on the vertical temperature gradient of longitudinally connected slab ballastless track on bridge in Autumn [J].Journal of Hunan University(Natural Sciences),2015,42(3):94- 99.

[16]TB 10002.1—2005,铁路桥涵设计基本规范 [S].

Optimization Design of Rivet Head for Shaft Riveting Assembly of Hub Bearing Unit

QUJieZHANGGuo-jieXUXiao-qin

(School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China)

Abstract:In order to overcome the nonlinearity and instability of the shaft riveting assembly process of wheel hub bearing units, an optimization strategy based on the surrogate model was proposed for the optimization design of the rivet head. In the investigation, first, the finite-element modeling parameters were determined through the tensile test, the ring upsetting test, the on-site axial feeding displacement test, the on-site axial riveting force test and the theoretical derivation about the space trajectory of the rivet head. Next, a comparison between the simulated and the tested results of the axial riveting force and the hub shaft's ultimate deformed shape was made to verify the effectiveness of the proposed finite element model. Then, on the basis of the existing design experiences and the life theory of hub bearing units, the parametric equations and the optimization objective were determined. Moreover, on the basis of the Latin hypercube sampling strategy and the finite element simulation results, a support vector machine regression model, which takes into consideration the maximum radial deformation of inner ring, the axial preload, the acting force between the hub shaft and the rivet head as well as the forming surface parameters of the rivet head, was established. Finally, a verification of the optimization design was performed, with an improved performance of the hub bearing unit being achieved.

Key words:hub bearing unit; shaft riveting assembly; surrogate model; support vector machine regression

doi：10.3969/j.issn.1000- 565X.2016.02.004

中图分类号：U 213.912

文章编号：1000- 565X(2016)02- 0020- 06

作者简介：戴公连(1964-)，男，教授，主要从事大跨度桥梁承载力研究.E-mail:daigong@vip.sina.com†通信作者： 苏海霆(1988-)，男，博士生，主要从事高速铁路系统温度场研究.E-mail:suhaiting1988@gmail.com

*基金项目：国家自然科学基金资助项目(51378503);高速铁路基础研究联合基金资助项目(U1334203);中国博士后科学基金资助项目(2014M552158);中国铁路总公司科技研究开发计划课题(2014T003-D);中南大学中央高校基本科研业务费专项资金资助项目(2015zzts060)

收稿日期：2015- 01- 09

Foundation items: Supported by the National Natural Science Foundation of China(51378503) and the China Postdoctoral Science Foundation(2014M552158)