基于多元线性回归的动态负荷模型参数实时选择*

黄玉龙　刘明波　陈迅

(1.暨南大学 电气信息学院， 广东 珠海 519070； 2.华南理工大学 电力学院， 广东 广州 510640；

3.广东电网公司 电力科学研究院， 广东 广州 510600)



基于多元线性回归的动态负荷模型参数实时选择*

黄玉龙1刘明波2陈迅3

(1.暨南大学 电气信息学院， 广东 珠海 519070； 2.华南理工大学 电力学院， 广东 广州 510640；

3.广东电网公司 电力科学研究院， 广东 广州 510600)

摘要：在分析负荷模型参数影响因素的基础上,基于多元线性回归法提出一种动态负荷模型参数实时选择法.首先，对一段时间内负荷的全部历史扰动实测数据进行负荷模型参数辨识，积累成模型参数数据库，并按照电压振荡幅值将其分为小扰动、一般扰动和大扰动负荷模型参数数据库；然后，根据仿真需要从相应类型的负荷模型参数数据库中用多元线性回归法搜索最匹配系统实时状况的负荷模型参数并分析其拟合精度；最后，用某城市群两个变电站的实测数据验证了所提方法的有效性和准确性.

关键词：动态负荷模型；时变性；多元线性回归；电压振荡幅度；扰动；拟合精度

负荷模型在电力系统研究中发挥着越来越重要的作用.精确的负荷建模使系统设计更经济，大扰动下的仿真精度更高，从而有利于提高控制与保护设备设置的精确度以及实时控制的准确性[1]，故此，负荷建模得到了广泛的研究.

由于综合负荷常由多样、时变的不同特性负荷组成成分构成[2]，负荷动态特性将随着时间、月份、季节、节假日、温度、电压等变化，准确负荷建模难度极大[3- 4].

文献[5]对照了早、中、晚负荷特性，以及工作日与周末负荷特性的变化情况；文献[6]指出不同运行状况下一些负荷参数大范围变化，需要实时辨识实际运行状况下的参数；文献[7]提到由于负荷组成随着日、周、季节、天气而变化，负荷建模困难；文献[8]也注意到负荷参数随时间的变化.

文献[2]提出一种多曲线参数辨识技术，并且研究其泛化能力以适应电力系统多数随机场景，但其难以表达负荷参数的随机变化，降低了建模精度.文献[9- 10]采用分类综合法解决负荷时变性，然而，有限分类不足以揭示一直变化中的负荷特性，不同分类之间还会有交集.文献[11]基于随机模糊聚类将负荷曲线分类，再用多曲线辨识技术辨识出每一类负荷曲线组相应的模型参数，得到多套模型参数，但仅用与当前时刻的远近或与当前时刻是否为相同类型作为依据选择负荷模型而忽略其他因素，会造成一定误判.

文献[12]利用强跟踪滤波和主导参数技术实现实时负荷建模，跟踪在线负荷模型参数的变化，但主导参数技术降低了负荷模型参数的维数，牺牲了一定的负荷拟合精度；且仅依据负荷节点电压选择当前基本负荷模型参数，忽略了其他影响因素.文献[13]基于在线综合负荷主导参数测辨方法提出区域综合负荷整体等值和参数测辨方案.但文献[12- 13]只能在系统发生扰动时启动负荷参数辨识进行系统安全仿真，在其他时刻不能辨识，不利于制定系统安全预防控制措施.

文献[14]指出随机参数辨识有助于解决负荷时变性问题；文献[2]推断：能反映负荷内在随机变化规律的负荷建模将是最好的.考虑风电接入后节点特性的不确定性，文献[15]提出了以有功功率为特性参考变量、基于概率统计的广义负荷节点稳态特性建模方法.

为了揭示动态负荷参数的实时变化规律，提高负荷模型精度，文中提出一种基于多元线性回归(MLR)的动态负荷参数选择方法，在历史负荷模型参数(LMPs)数据库中寻找最匹配实时运行状况的负荷参数，并在某城市两变电站进行了分析验证.该方法突破了传统分类综合法和多曲线参数辨识法的局限，LMPs不再分为有限种类，而是由线性回归的样本容量——参数数据库的大小决定，克服了在线主导参数测辨方法只能在系统发生扰动时启动负荷参数辨识进行系统安全仿真的不足.

1动态负荷参数实时选择方法

1.1形成LMPs数据库

首先，根据研究目的决定所采用的负荷模型[16].暂态稳定分析中考虑感应电动机负荷的动态特性，常采用计及感应电动机机电暂态的动态负荷模型[17]，对于电压稳定，无功负荷特性更重要些.在我国电网中电动机负荷一般占有较大比例，常用ZIP并联电动机模型进行电压稳定仿真[18- 20].文中选择易集成于电力系统分析工具中的ZIP并联电动机综合负荷模型作为综合负荷模型结构，为电力系统稳定分析与控制所用，其详细等值电路和微分代数方程见文献[2].

然后，按照一定的负荷建模方法辨识LMPs.文中利用文献[21]提出的微分进化算法对全部历史扰动实测数据进行LMP辨识，该算法全局搜索能力强.积累一定历史时间段内相应的LMPs建成模型参数数据库；此后，每当实测到新的扰动数据时，就辨识LMPs更新参数数据库.在线负荷动态特性一直在变化之中.由于扰动发生的随机性，利用各扰动实测数据辨识出的LMPs就可反映负荷动态特性的随机变化，而且LMPs数据库越大，就越能全面地表现出负荷动态特性的变化情况.进而，利用1.2节提出的MLR方法在该数据库中选择最适合当前系统状况的LMPs.

1.2动态负荷参数MLR选择方法

随着实测数据及其负荷参数数据的积累，在表面不相关的负荷数据里发现统计规律就变得更容易.文献[22]指出，在负荷建模中应当探索基于小数据集上的统计学习理论[23]和建模技术，也指出可以应用海量数据下的统计规律指导基于实测数据的负荷建模过程.

多元线性回归方法用来建立多个变量与响应变量之间的不确定关系.文献[24]用其进行短期负荷预测，文献[25]利用逐步多元线性回归法，根据未安装负荷记录装置点的负荷大致组成推测出此点的负荷模型.

负荷动态特性将随着时间、月份、季节、节假日、温度、电压及其变化幅度、负荷有功功率、无功功率、视在功率及功率变化幅度等随机变化.为了揭示负荷动态特性的实时统计变化规律、提高建模精度，本节提出一种基于多元线性回归[26- 27]的负荷参数选择方法，在历史LMPs数据库中寻找最匹配实时运行状况的负荷参数.

不同扰动种类情况下，功率振荡幅度不同；甚至同类扰动下，功率振荡幅度也不同.对于振荡幅度很小的扰动k，误差函数值也很小，但相对振荡幅度来讲误差可能很大；反之依然.为了衡量不同扰动之间误差函数的相对大小，将误差函数修改为规格化误差函数：

(1)

(2)

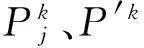
(3)

(4)

(5)

Y=β0+β1X1+β2X2+…+βpXp+ε

(6)

在Ns个历史LMPs组成的参数数据库中取出一模型参数，用该参数仿真其余的Ns-1个扰动计算修正误差函数E′k，相当于做了Ns个实验，相应的修正误差函数值Y为：Y=[E′1E′2…E′Ns]T，ρ个自变量Ns个扰动下对应值写成向量形式为：X1、X2、…、Xp，即X1=[X11X12…X1Ns]T等.

1.2.1变量标准化

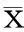
(7)

(8)

1.2.2多元线性回归

将Y和X1,X2,…,Xp代入式(6)，得到矩阵形式回归模型：

(9)

假设ε的Ns个分量都满足正态性、独立性和方差齐性.β的最小二乘估计[27]可用下式表示：

(10)

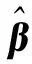
(11)

σ2的无偏估计[27]为

(12)

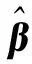
1.2.3检查离群数据

1.2.4变量选择

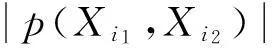
1.2.5可决系数

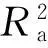
(13)

(14)

(15)

1.2.6回归方程的F检验

E′与X1,X2,…,Xp之间的线性显著性用F检验，零假设为H0∶β1=β2=…=βp=0.采用的统计量F服从F分布，如式(16)所示：F=(SSR/p)/[SSE/(Ns-p-1)]～F(p,Ns-p-1)

(16)

对给定的显著性水平α，若F>F1-α(p,Ns-p-1)，拒绝H0，认为回归方程显著，可被采用.

1.2.7回归系数的t检验

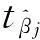
(17)

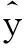
(18)

对应水平为1-α置信区间的两个端点则为

(19)

1.2.8负荷参数实时选择流程

负荷参数实时选择流程如图1所示.

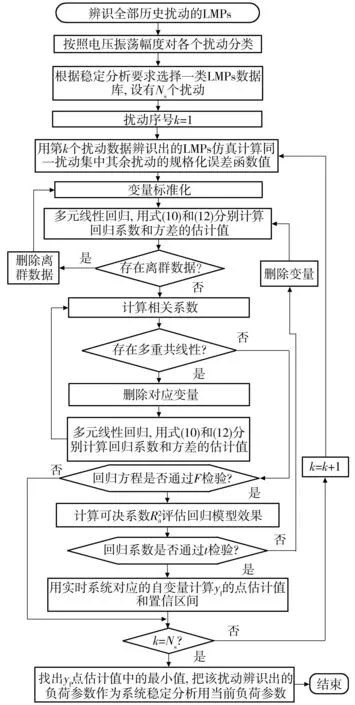
图1　负荷参数实时选择流程图

Fig.1Flowchart of real-time dynamic load model parameter selection

首先，按照微分进化算法对最近一时间段内的全部历史扰动数据进行负荷参数辨识，建立LMPs数据库；然后，对各个扰动按照电压振荡幅度ΔUkmax/ΔUkmin进行分类.

负荷模型结构与扰动幅度大小存在一定关系.ZIP并联电动机综合负荷模型及参数适用于电压在0.8～1.2 p.u.小范围波动的情况，可用于大扰动暂态功角稳定和暂态电压稳定分析[18- 19].电压及频率大范围波动、中长期动态过程下的广谱负荷建模[28]需要考虑低压减载、低频减载[20]、低压继电器动作[1]等作用，将在后续研究中继续进行，文中不做深入讨论.故此，将扰动分为小扰动集Zs、一般扰动集Zc和大扰动集Zl，分别见式(20)-(22)，把LMPs数据库相应地分为小扰动、一般扰动和大扰动参数数据库.

Zs={k|(ΔUkmax<0.01)∩(ΔUkmin<0.01)}

(20)

(21)

Zl={k|0.2≤ΔUkmin}

(22)

然后，采用每组LMPs仿真同一扰动集中其余扰动，建立回归模型.最后，按照各个扰动建立起来的多元线性回归模型对当前系统运行点进行预测，找出响应变量预测点估计值中的最小值，把用该扰动数据辨识出的LMPs作为系统当前LMPs.

经验认为，MLR中最小样本容量Ns至少为3(p+1)，不能满足时必须不小于p+1=11[29]，也可以根据需要满足的估计量方差确定最小样本容量[30].此处，样本来源于负荷模型参数库备选参数，随着数据库的积累样本容量不断增大，LMPs备选数量将远大于分类综合法中的有限几类.

由于MLR计算量很小，参数选择程序可以每5min左右计算一次，及时为系统电压稳定和暂态稳定计算等提供负荷模型准确参数.所有变电站各自独立完成上述参数实时选择过程.当选择完电力系统全部相关节点的LMPs后，进行相应的在线稳定分析，分析结果将更加符合系统实际动态特性.特别指出，除了电压暂降/升幅度X6/X7、功率振荡幅度X10外，MLR自变量都是可以实时实测的，而X6/X7和X10可以根据仿真中的预设扰动类型、负荷点距离故障点电气距离远近等预先设置.故此，不论是否有当前系统的实测扰动数据，都可以用MLR法选择匹配当前系统的LMPs.

2MLR选择法的适应性和效果分析

2.1MLR选择法适应性分析

无论采用何种负荷建模方法，只要提供历史扰动中的负荷实测数据，就可以计算出仿真有功、无功功率值与实测值之间偏差的规格化误差函数，继而可以用MLR法选择匹配当前系统的负荷参数.所以在变电站安装负荷相关测量装置的情况下，多元线性回归动态负荷参数选择方法不受负荷模型结构、负荷建模方法的影响.

为保证数据的有效性，LMPs数据库需要循环滚动更新积累近若干年(例如10年)LMPs数据建立而成，及时反映负荷结构和动态特性等的变化.根据具体系统扰动发生频率、负荷增长速度和负荷结构变化速度选择更新周期，及时舍弃无效数据，同时满足最小样本容量的要求.若待建模负荷结构发生大幅度突变，采用MLR法不一定能马上将其反映出来，可能存在一定的滞后性；但随着时间的推移，积累足够多的样本后同样是可以将其表现出来的.事实上，条件允许的变电站可以参照负荷结构分析[31]，尝试将各负荷结构比例作为一个回归因素加入到MLR模型中进行在线负荷参数选择，这应当可以减轻对负荷结构大幅突变反映滞后造成的参数选择准确度下降问题，也是我们将来要继续进行的研究内容之一.

2.2优选出的LMPs拟合精度分析

下面分析MLR选择出的LMPs拟合精度，并与多曲线拟合参数辨识法比较.设一定电压输入下实际功率测量值为[PQ]T，与噪声无关的负荷动态输出为[Pn_ fQn_ f]T，两者的平方误差可以被分解为模型误差和噪声方差，而负荷模型误差可被分解为偏移误差和模型方差误差[2].一般来讲，模型结构越复杂，参数越多，偏移误差单调减少.但由于模型方差误差与模型参数数量成比例，太复杂的负荷模型结构会导致模型的泛化能力降低.文中在模型参数数据库中选择参数，数据库中每一模型参数用各自扰动数据辨识出，不要求参数的泛化能力，所以所提出的负荷模型误差可以随着负荷模型复杂度升高单调降低，这也符合美国西部电网协调委员会对基于物理模型的负荷建模的要求[32].

文献[2]采用多曲线拟合参数辨识法最小化目标函数Mu1(见式(23))，使得辨识出的负荷参数尽量适合全部Ns个实测数据，此处用E′k代替均方根误差表示拟合精度.

(23)

其中，Wk是扰动k量测的权重系数.

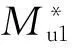
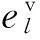
(24)

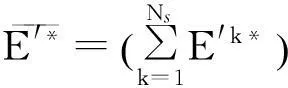
3实例分析

以某大城市两个220 kV变电站A和B为例来说明MLR参数选择法的可行性和准确性.采用的计算机配置为Intel双核2.4 GHz CPU，4 GB内存.变电站A数据取自2010年2月至2012年5月，总共有49个扰动数据；变电站B数据取自2010年2月至2011年9月，总共有56个扰动数据.功率和电压的基准值分别为SB=100 MV·A和UB=220 kV.

采用和文献[21]一样的模型参数范围，按照微分进化算法对两变电站全部历史扰动数据进行负荷模型参数辨识，建立LMPs数据库.按照式(20)-(22)将两个变电站的全部扰动分为3个扰动集，其中变电站A、B一般扰动集ZC中分别有31、24个扰动.本算例只考虑一般扰动集.

然后，用MLR法预测选择实时动态负荷参数.由于模型的预测能力只能在新的实测数据上验证，将数据集ZC分为训练数据集和验证数据集.训练数据集用来求解MLR，验证数据集用来验证MLR法参数选择的准确性.按照扰动发生时间顺序排列后，将变电站A、B一般扰动集ZC中最后3个扰动归入验证数据集，那么两变电站的训练扰动数量Ns分别为28和21.变电站A接近最小样本容量3(p+1)=33要求，变电站B却明显不足，但两者都达到了必须满足的条件p+1=11.需要注意的是，此处通过比较最后3个扰动预测值yf与实际值来验证MLR方法的预测效果.

给定显著性水平α=0.05，变电站A全部扰动的回归方程通过F检验；变电站B第6、10、21次扰动的回归方程不能通过F检验，剩下18个回归模型.这样，变电站A、B分别有28组和18组备选LMPs，远大于分类综合中的有限几类.

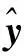
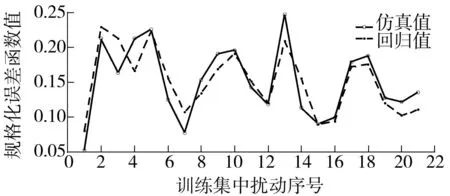
图2　变电站B第一次扰动yi与i的对照

显然，规格化误差函数值在不同的运行状态下起伏变化很大，误差值并不一定随着时间的延迟而变大.

表1给出了两变电站两次扰动对应的回归系数和可决系数.

表1两变电站两次扰动对应的回归系数、可决系数和计算时间

Table 1Regression parameters，coefficients of determination and computational time according to two disturbances for the two substations

变电站扰动序号回归系数β0β1β2β3β4β5β6β7β8β9β10R2a时间/sAB10.1974-0.0218-0.00550.1432-0.14830.0277—0.02270.04270.06990.03060.83140.32720.1914-0.01660.00850.1120-0.10910.0025—0.01380.04950.06770.01620.82060.31210.1510-0.02300.0173—-0.00300.02200.0343-0.00330.04680.0213-0.60880.31220.2151-0.03030.0023—-0.02380.05070.0072-0.0071-0.0641—0.01910.69330.281

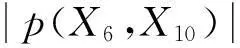
通过建立的回归模型，得到变电站A、B验证数据集对应的点估计值和1-0.05置信区间上下限.图3给出用变电站B第一次扰动建立的MLR预测效果，yf的估计值围绕着由仿真得到的实际值.

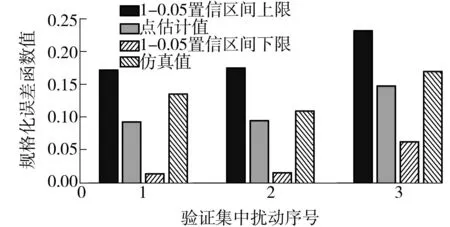
图3　变电站B第一次扰动建立的MLR预测效果

Fig.3MLR prediction effect based on the 1st disturbance of substation B

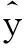
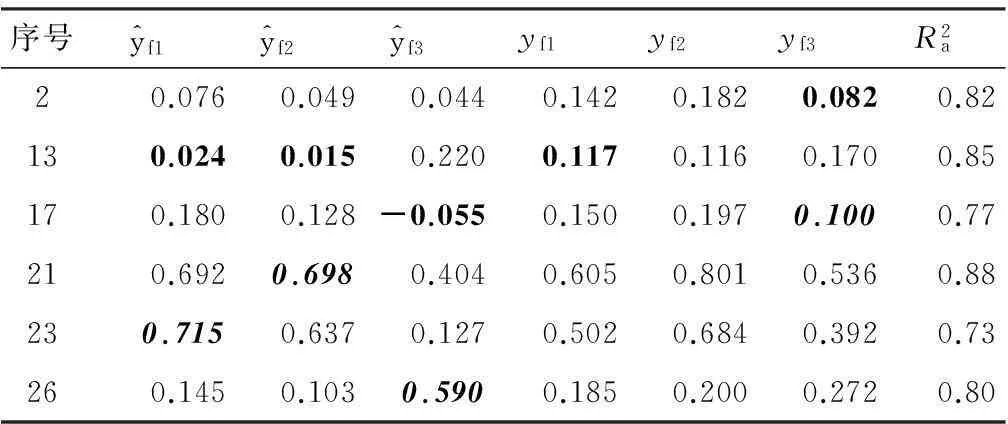
表2　变电站A yf估计效果

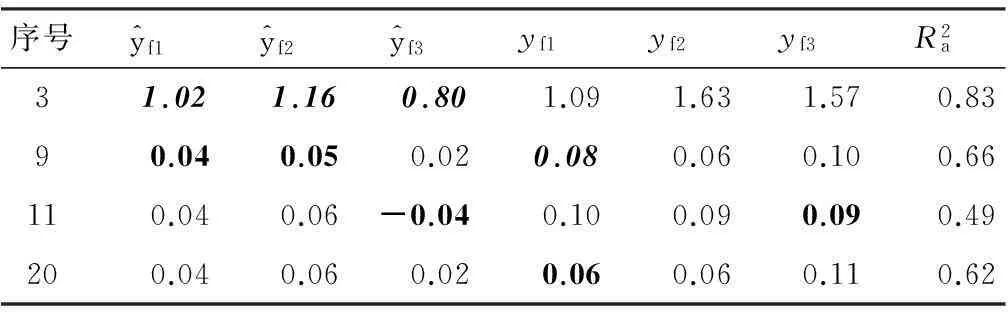
表3　变电站B yf估计效果

表4中列出了变电站A部分扰动对应的自变量，可以看出，第13、29和30次扰动发生时间、温度、U0、P0和Q0比较接近，这是负荷动态特性一致的必要但非充分条件.表4中第22次扰动的这些变量取值同样接近第29和30次的.这也验证了用回归选择法解决负荷参数时变性问题比用分类综合法效果更准确.表4中第21次和第31次扰动时刻最

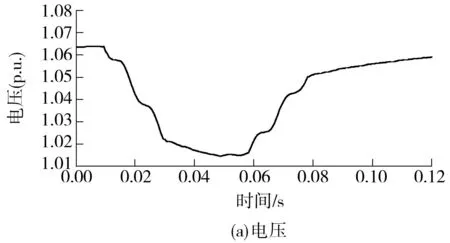
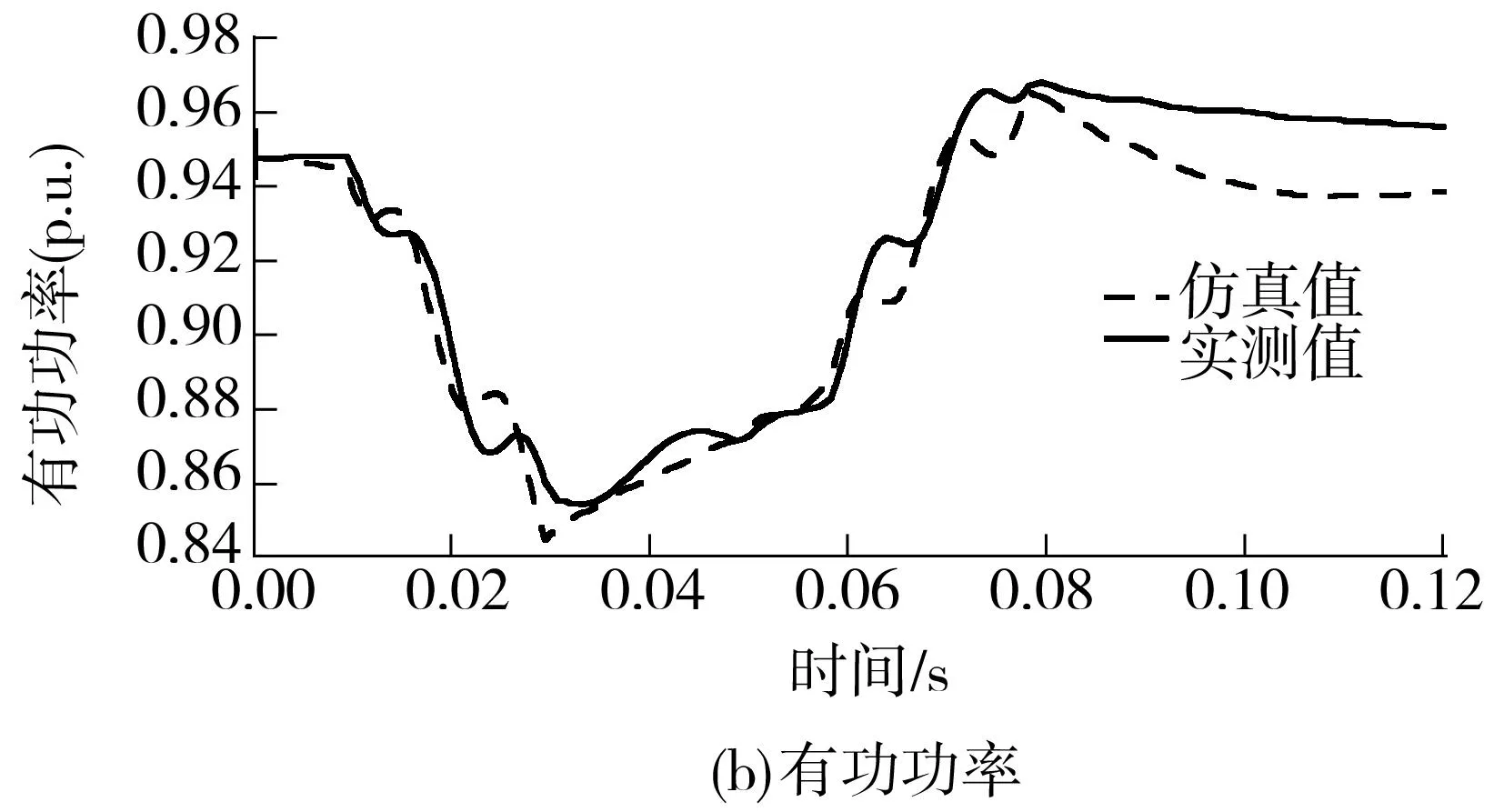
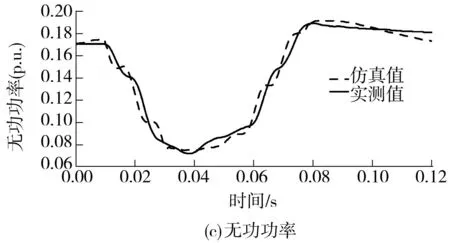
图4用变电站B第9次扰动数据建立的LMPs仿真第22次扰动的电压和功率

Fig.4Voltage and power of substation B based on the 22th disturbance data using the load model parameters identified by the 9th disturbance data

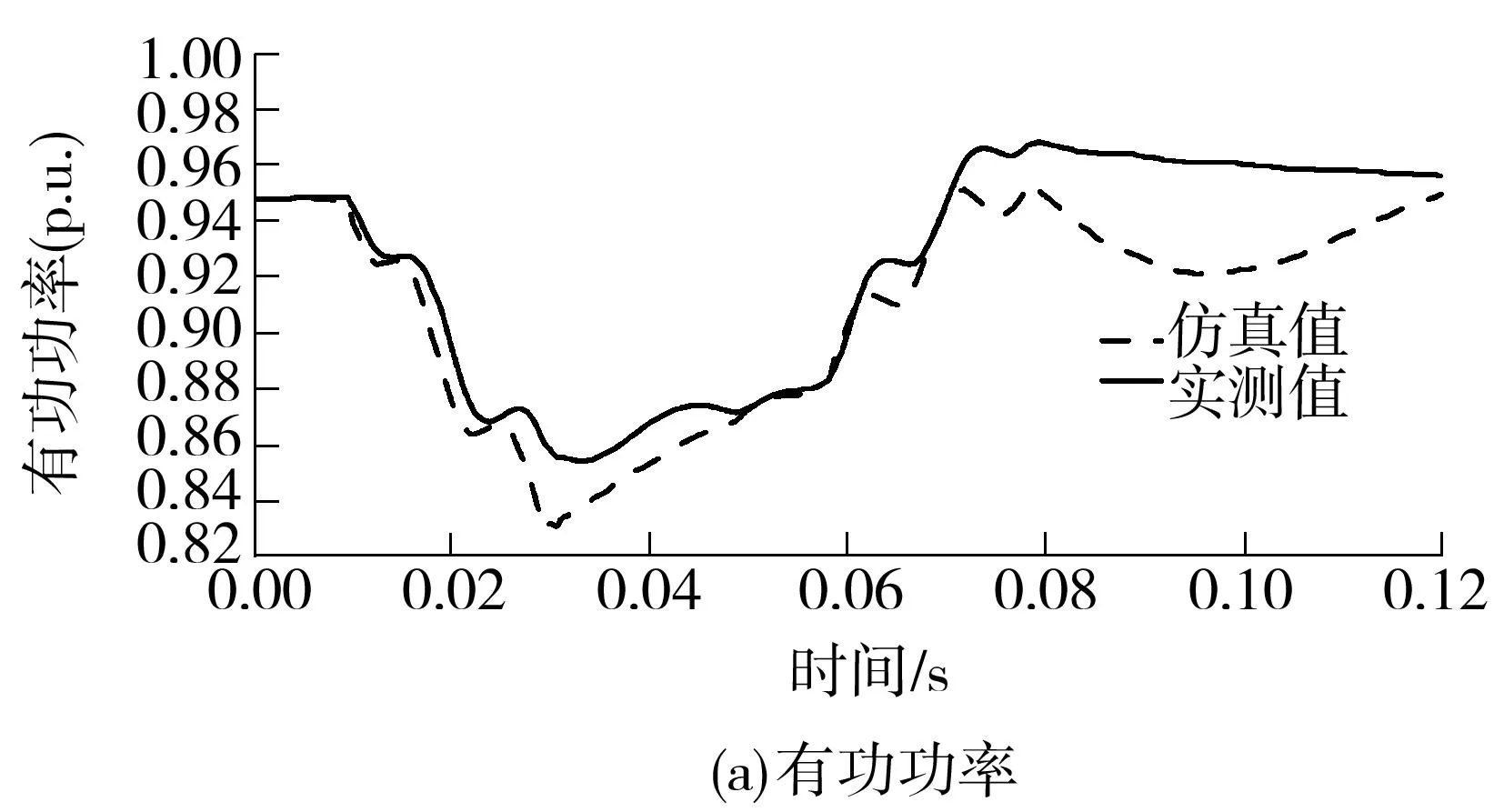
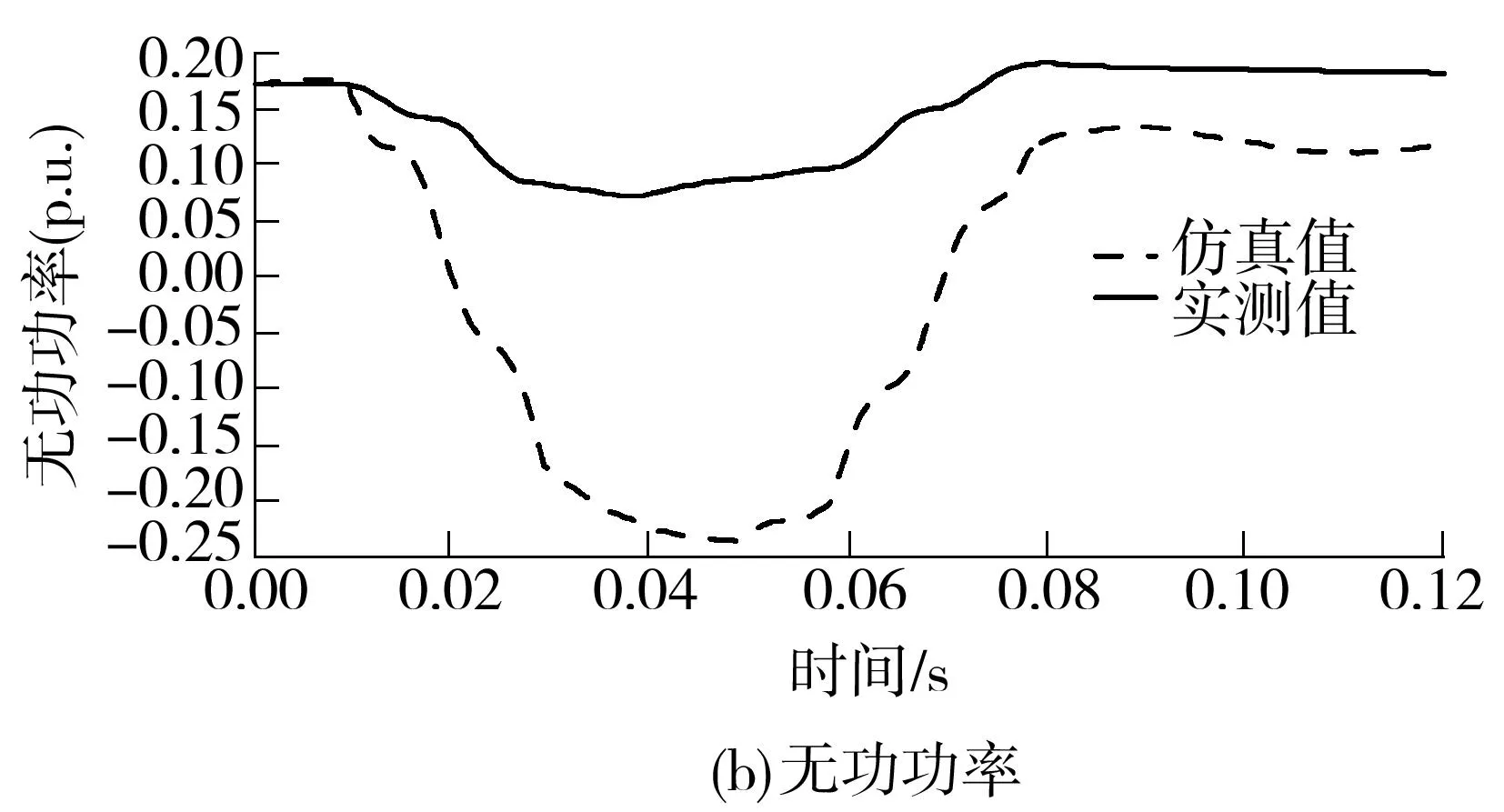
图5用变电站B第3次扰动数据建立的LMPs仿真第22次扰动的功率

Fig.5Power of substation B based on the 22th disturbance data using the load model parameters identified by the 3th disturbance data

相近，但第21次扰动数据辨识出的LMPs被选作第31次扰动发生时刻的负荷参数，仿真得到yf为0.536(见表2)，误差很大.从表4中可见第21次和第31次扰动对应的温度、有功和无功差异较大，负荷特性相差很大.文献[11]仅用与当前时刻的远近或与当前时刻是否为相同类型作为依据选择负荷模型，可能会造成误判.

表4变电站A数据集ZC中部分扰动对应的自变量

Table 4Part predictor values of disturbances in setZCof substation A

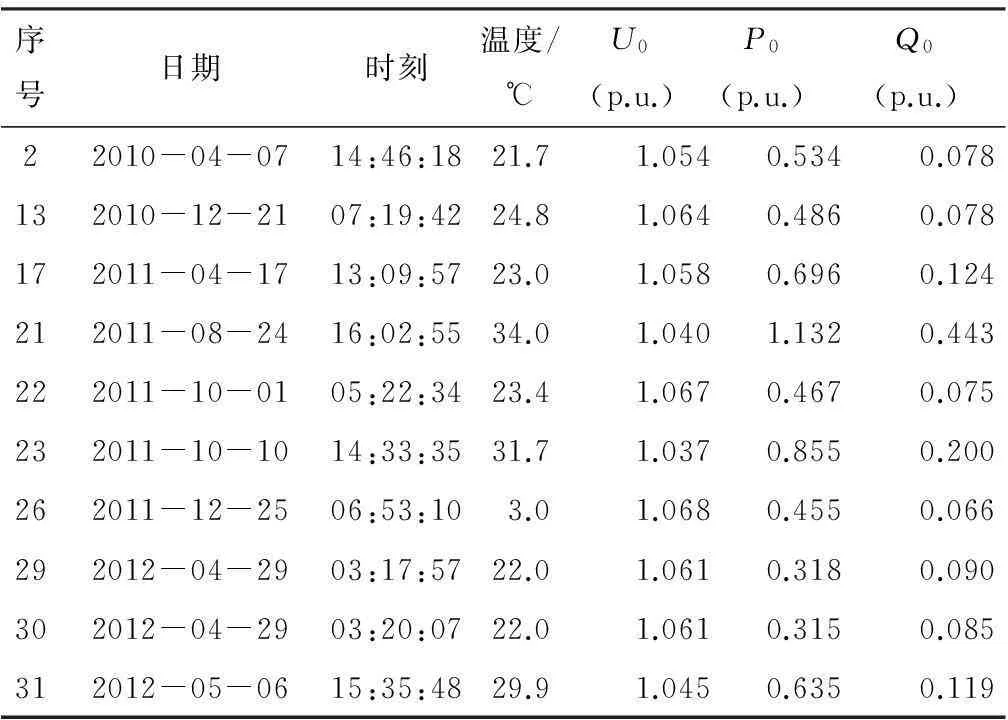
序号日期时刻温度/℃U0(p.u.)P0(p.u.)Q0(p.u.)22010-04-0714:46:1821.71.0540.5340.078132010-12-2107:19:4224.81.0640.4860.078172011-04-1713:09:5723.01.0580.6960.124212011-08-2416:02:5534.01.0401.1320.443222011-10-0105:22:3423.41.0670.4670.075232011-10-1014:33:3531.71.0370.8550.200262011-12-2506:53:103.01.0680.4550.066292012-04-2903:17:5722.01.0610.3180.090302012-04-2903:20:0722.01.0610.3150.085312012-05-0615:35:4829.91.0450.6350.119

下面比较多曲线拟合参数辨识法[2]和MLR参数选择法中负荷模型在新数据上的拟合精度，变电站A和B的比较结果见表5.

表5在新运行点上负荷模型的拟合精度比较

Table 5Comparison of load model fitting performance on fresh data

变电站E'*———^eA0.0730.224B0.0620.267

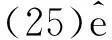
(25)

表1中的MLR计算时间完全满足在线计算速度的要求.即使考虑到将来LMPs数据库的增大，MLR计算也足以在5 min内完成，及时为系统电压稳定和暂态稳定计算等提供负荷模型准确参数.

4结论

文中基于MLR提出一种负荷模型参数实时选择法，解决LMPs时变性问题.以某城市两变电站为例，验证了该方法能够比较准确、方便地实现负荷参数的在线选择.根据扰动幅度值将扰动分类后，能够选择到最匹配或接近最匹配系统实时状况的LMPs，优选到的LMPs拟合精度得到极大提升；随着LMPs数据库的增大，MLR法的选择准确性会提高；线性回归计算量小，计算时间可以满足在线选择LMPs的需求，为系统在线稳定分析与控制提供准确LMPs；参数选择方法不受负荷模型结构、负荷建模方法的影响，不受当前系统是否发生扰动的限制.

参考文献：

[1]KUNDUR P.Power system stability and control [M].New York:McGraw-Hill，1993:306- 311.

[2]HE R M，MA J，DAVID J H.Composite load modeling via measurement approach [J].IEEE Transactions on Power System，2006，21(2):663- 672.

[3]BAI H，ZHANG P，AJJARAPU V.A novel parameter identification approach via hybrid learning for aggregate load modeling [J].IEEE Transactions on Power System，2009，24(3):1145- 1154.

[4]AI Q，GU D，CHEN C.New load modeling approaches based on field tests for fast transient stability calculations [J].IEEE Transactions on Power System，2006，21(4):1864- 1873.

[5]SHACKSHAFT P，SYMONS O C，HADWICK J G.Gene-ral purpose model of power system loads [J].Proceedings of the Institution of Electrical Engineers，1977，124(8):715- 723.

[6]LIU Q S，CHEN Y P，DUAN D F.The load modeling and parameter identification for voltage stability analysis [C]∥Proceedings of International Conference on Power System Technology.New York:Institute of Electrical and Electronics Engineers Inc.，2002:2030- 2033.

[7]WEN J Y，JIANG L，WU Q H，et al.Power system load modeling by learning based on system measurements [J].IEEE Transactions on Power Delivery，2003，18(2):364- 371.

[8]JU P，WU F，SHAO Z Y，et al.Composite load models based on field measurements and their applications in dynamic analysis [J].IET Generation，Transmission and Distribution，2007，1:724- 730.

[9]鞠平，金艳，吴峰，等.综合负荷特性的分类综合方法及其应用 [J].电力系统自动化，2004，28(1):64- 68.

JU Ping，JIN Yan，WU Feng，et al.Studies on classification and synthesis of composite dynamic loads [J].Automation of Electric Power Systems，2004，28(1):64- 68.

[10]石景海，贺仁睦.基于量测的负荷建模—分类算法 [J].中国电机工程学报，2004，24(2):78- 82.SHI Jing-hai，HE Ren-mu.Measurement-based load modeling sorting algorithm [J].Proceedings of the CSEE，2004，24(2):78- 82.

[11]林济铿，刘露，张闻博，等.基于随机模糊聚类的负荷建模与参数辨识 [J].电力系统自动化，2013,37(14):50- 58.

LIN Ji-keng，LIU Lu，ZHANG Wen-bo，et al.Load mo-deling and parameter identification based on random fuzziness clustering [J].Automation of Electric Power Systems，2013,37(14):50- 58.

[12]ZHENG J，WANG X，ZHU S.A novel real-time load modeling method for fast large-disturbance and short-term voltage stability analysis [J].International Tran-sactions on Electrical Energy Systems，2013，23:1373- 1395.

[13]张树卿，韩英铎，于松泰，等.区域综合负荷动态等值参数在线测辨关键技术 [J].电力系统自动化，2012,36(19):114- 121.

ZHANG Shu-qing，HAN Ying-duo，YU Song-tai，et al.Key techniques for composite load area integral equivalence and online parameter identification [J].Automation of Electric Power Systems，2012,36(19):114- 121.

[14]KARLSSON D，HILL D J.Modeling and identification of nonlinear dynamic loads in power systems [J].IEEE Transactions on Power System，1994，9(1):157- 166.

[15]张旭，梁军，贠志皓，等.考虑风电接入不确定性的广义负荷建模及应用 [J].电力系统自动化，2014，38(20):61- 67.

ZHANG Xu，LIANG Jun，YUN Zhi-hao，et al.Genera-lized load modeling and its application considering uncertainty of wind power integration [J].Automation of Electric Power Systems，2014，38(20):61- 67.

[16]鞠平，马大强.电力系统负荷建模 [M].北京:中国电力出版社，2008:4- 7.

[17]倪以信，陈寿孙，张宝霖.动态电力系统分析 [M].北京:清华大学出版社，2002:85- 87.

[18]井艳清，李兴源，郭晓鸣，等.考虑感应电动机负荷模型的暂态电压稳定快速判据 [J].电力系统自动化，2011，35(10):10- 14.

JING Yan-qing，LI Xing-yuan，GUO Xiao-ming，et al.A quick criterion for transient voltage stability considering induction motor load models [J].Automation of Electric Power Systems，2011,35(5)：10- 14.

[19]林舜江，李欣然，刘杨华，等.考虑负荷动态模型的暂态电压稳定快速判断方法 [J].中国电机工程学报，2009，29(4):14- 20.

LIN Shun-jiang，LI Xin-ran，LIU Yang-hua，et al.Method for transient voltage stability quick judgment considering load dynamic model [J].Proceedings of the CSEE，2009，29(4):14- 20.

[20]周双喜，朱凌志，郭锡玖，等.电力系统电压稳定性及其控制 [M].北京:中国电力出版社，2009:288- 290.

[21]黄玉龙，陈迅，刘明波，等.动态负荷模型参数辨识的微分进化算法 [J].电工技术学报，2013，28(11):270- 277.

HUANG Yu-long，CHEN Xun，LIU Ming-bo，et al.Differential evolution algorithm for dynamic load model parameter identification [J].Transactions of China Electrotechnical Society，2013，28(11):270- 277.

[22]RADONJA P，STANKOVIC S，POPOVIC Z.Specific process models derived from extremely small data sets and general process models [C]∥Proceedings of the 7th Seminar Neural Network Applications Electrical Engineering.New York:Institute of Electrical and Electronics Engineers Inc，2004:267- 272.

[23]VAPNIK V N.The nature of statistic learning theory [M].New York:Springer-Verlag，1995.

[24]SOLIMAN S A，PERSAUD S，El-NAGAR K，et al.Application of least absolute value parameter estimation based on linear programming to short-term load forecasting [J].International Journal of Electrical Power and Energy System，1997，19(3):209- 216.

[25]郑晓雨，贺仁睦，马进.逐步多元回归法在负荷模型扩展中的应用 [J].中国电机工程学报，2011，35(10):72- 77.

ZHENG Xiao-yu，HE Ren-mu，MA Jin.Application of stepwise multiple regression to load model extention [J].Proceedings of the CSEE，2011，31(4):72- 77 .

[26]DEVORE Jay L.Probability and statistics for engineering and the sciences [M].Beijing:Higher Education Press，2004:488- 607.

[27]夏宁茂.新编概率论与数理统计 [M]．上海:华东理工大学出版社，2011:266- 285.

[28]鞠平.电力系统建模理论与方法 [M].北京:科学出版社，2010:244- 246.

[29]张小富，侯纲.基于多元线性回归模型的西安住宅价格泡沫研究 [J].价格月刊，2012，11(426)：41- 44.

ZHANG Xiao-fu，HOU Gang.Research on housing price bubble of Xi’an based on multiple linear regression model [J].Prices Monthly，2012，11(426)：41- 44.

[30]俞纯权.回归估计样本容量的确定 [J].数理统计与管理，1995，14(4)：33- 36.

YU Chun-quan.An approach for determining sample size in regression estimate [J].Journal of Applied of Statistics and Management，1995，14(4)：33- 36.

[31]江峰青，郑淮，李荣民.上海电网负荷结构分析及特性预测 [J].华东电力，2008，36(9):51- 52.

JIANG Feng-qing，ZHENG Huai，LI Rong-min.Structure analysis and characteristic forecasting for loads of Shanghai Power Grid [J].East China Electric Power，2008，36(9):51- 52.

[32]WECC load modeling task force [EB/OL].(2014- 07- 01)[2014- 07- 31].http:∥www.wecc.biz/committees/StandingCommittees/PCC/TSS/MVWG/111306/Lists/Minutes/1/Workshop%20Load%20Modeling.pdf.

Real-Time Selection of Dynamic Load Model Parameters Based on Multiple Linear Regression

HUANGYu-long1LIUMing-bo2CHENXun3

(1.Electrical and Information College, Jinan University, Zhuhai 519070, Guangdong, China;2.School of Electric Power,South China University of Technology,Guangzhou 510640,Guangdong,China;3.Electric Power Research Institute of Guangdong Power Grid Corporation,Guangzhou 510600,Guangdong,China)

Abstract:This paper analyzes the factors influencing the load model parameters and proposes a real-time selection method of dynamic load model parameters based on the multiple linear regression. In the investigation, first, all historical load disturbance data measured in a certain duration are identified to obtain the load model parameters, and the identified parameters are used to construct a model parameter database that is further classified into three sub-databases respectively corresponding to small, common and large disturbances. Then, the parameters matching the real-time operation condition best are found from the sub-databases with correct disturbance type and the fitting accuracy is further analyzed.Finally,the effectiveness and accuracy of the proposed method are verified with the field measurement data collected from two substations in a metropolitan area in China.

Key words:dynamic load model;time-variability;multiple linear regression;voltage oscillation magnitude;disturbance;fitting accuracy

doi：10.3969/j.issn.1000-565X.2016.02.016

中图分类号：TM 71

文章编号：1000- 565X(2016)02- 0107- 10

作者简介：黄玉龙(1976-)，男，博士，讲师，主要从事负荷建模，电力系统优化、运行与控制等的研究.E-mail：thuangyulong@jnu.edu.cn

*基金项目：国家自然科学基金资助项目(51377072)

收稿日期：2015- 06- 17

Foundation item: Supported by the National Natural Science Foundation of China(51377072)