齿轮噪声干扰及变转速下的滚动轴承故障诊断*

赵德尊　李建勇　程卫东

(北京交通大学 机械与电子控制工程学院， 北京 100044)



齿轮噪声干扰及变转速下的滚动轴承故障诊断*

赵德尊李建勇程卫东†

(北京交通大学 机械与电子控制工程学院， 北京 100044)

摘要:齿轮噪声以及变转速运行是干扰滚动轴承故障诊断的常见因素，针对上述两种因素同时对滚动轴承故障诊断的干扰，引入了集合经验模态分解(EEMD)方法以去除轴承信号中的齿轮噪声，将齿轮峰值啮合倍频(IDMM)等效为滚动轴承的瞬时转频，阶比跟踪以去除转速变化对滚动轴承故障诊断的影响，并将此方法命名为基于EEMD和IDMM的滚动轴承故障诊断方法.仿真和实测信号分析证明该方法能有效去除齿轮噪声和转速变化对滚动轴承故障诊断的影响，同时提高故障特征阶比的幅值，节省转速测量装置.

关键词：变转速；齿轮噪声；滚动轴承；故障诊断；集合经验模态分解；齿轮峰值啮合倍频

实际工况中，变转速工作机械设备普遍存在[1]，这种情况下滚动轴承的故障冲击将失去其原有的周期性，现有的以傅里叶变换为基础的包络分析技术将不再适用.另外，当对齿轮箱内或者齿轮箱附件的轴承进行健康检测时，由于齿轮啮合振动信号具有较高的幅值，容易掩盖滚动轴承的冲击特征，将严重影响滚动轴承健康状况的监测.因此在滚动轴承故障诊断之前消除齿轮噪声以及转速变化的干扰具有十分重要的现实意义.

阶比跟踪技术[2- 6]是处理变转速工作模式的有效方法，其思想是获得相对于参考轴的恒定角增量采样，将时域的非周期信号转化为角域周期信号以消除转速变化对振动信号的影响.常用的阶比跟踪方法有硬件阶比跟踪法、计算阶比跟踪法以及基于瞬时频率估计的阶比跟踪法等[3- 6].其中，基于瞬时频率估计的阶比跟踪算法因克服了硬件安装空间及安装成本对计算阶比跟踪以及硬件阶比跟踪的限制，近年来得到很多学者的关注.然而对于齿轮和故障轴承混合信号而言，高幅值齿轮噪声淹没了表征滚动轴承转频的信息.基于瞬时故障特征频率的方法难以从混合信号中提取到滚动轴承的转频信息.Wang等[7]根据齿轮峰值啮合倍频(IDMM)趋势线易于从原始信号中提取这一特性，将该趋势线用于构造ANC算法的参考信号.文中引入IDMM趋势线这一概念，并将其等效为滚动轴承转频.可行性主要表现在以下两个方面：(1)齿轮峰值啮合倍频具有较高的幅值，可以直接从混合信号的时频图中提取；(2)齿轮转频与轴承转频具有固定的比例关系，具体数值可由齿轮传动比计算.

经验模态分解(EMD)是由Huang等[8]提出的一种自适应信号分解方法.它基于信号的局部特征，将原始信号从高频到低频分解成有限个具有物理意义的固有模态函数，即本征模态函数(IMF).然而，EMD算法存在一些缺陷，其中一个主要的问题是模态混叠[9- 10].为抑制模式混叠，Wu等[11]提出了集合经验模态分解(EEMD)方法，该方法是一种噪声辅助的数据分析方法，利用高斯白噪声频率均匀分布的统计特性，在原始信号中添加特定的高斯白噪声以消除间断，促进抗混分解，有效抑制模式混叠现象.EEMD一经提出得到了很多学者的关注，并广泛应用于信号处理.彭畅等[12]提出了基于EEMD、度量因子和快速谱峭度图的滚动轴承故障诊断方法，该方法将轴承信号进行EEMD分解，通过度量因子筛选出含有故障信息的IMF分量，进而降低噪声的干扰.曹冲锋等[13]将EEMD算法用于大型旋转机械非平稳信号的降噪，克服了EMD降噪方法对脉冲干扰下振动信号滤波能力的不足，弥补了小波降噪算法对调幅调频信号处理过程中存在的特征波匹配的缺陷.李昌林等[14]将EEMD与Laplace小波相结合，以消除多阶模态冲击响应对Laplace小波相关滤波的影响，取得了较好的效果.唐贵基等[15]提出了基于EEMD降噪和1.5维能量谱的故障诊断方法，顺利提取到滚动轴承的故障特征频率信息.

针对齿轮噪声干扰和变转速两种影响因素并存状态下滚动轴承故障诊断这一问题，文中将EEMD算法和IDMM趋势线相结合，提出了基于EEMD和IDMM的滚动轴承故障诊断方法.该方法首先对混合信号进行短时傅里叶变换得到时频图，利用峰值搜索算法从中提取齿轮峰值啮合倍频趋势线，将该趋势线等效为轴承转频对混合信号进行角域重采样；其次确定EEMD参数，对重采样信号进行EEMD分解得到本征模态函数之和；再次计算各IMF分量的峭度值，选取峭度值最大的IMF分量进行后续分析；最后对选取的IMF分量进行包络谱分析，根据包络谱及滚动轴承故障特征系数确定滚动轴承故障类型.

1理论背景

1.1EEMD算法

EEMD算法是一种噪声辅助的数据分析方法，它利用高斯白噪声频率均匀分布的统计特性，在原始信号中多次添加特定的高斯白噪声以消除间断，促进抗混分解，有效抑制模式混叠现象.EEMD算法中运算次数以及白噪声标准差大小对处理效果的好坏有至关重要的影响.因为当噪声标准差过大时，将影响信号中高频成分的极值点分布，而当噪声标准差较小时，处理效果不理想.另外，运算次数越多处理效果将越好，然而同时会面临计算量大的困扰.Huang等[8,11]认为：当运算次数I=100时，大部分情况下噪声幅值的标准差为信号标准差的0.2倍.文中将I设为100，高斯白噪声幅值的标准差设为0.2.EEMD分解的步骤如下：

(1)确定运算次数I(I>1)以及白噪声ni(t)(i=1，2,…,I)的参数(均值为0，幅值的标准差为常数)；

(2)将具有特定幅值的白噪声ni(t)加入到原始信号x(t)中，即

xi(t)=x(t)+ni(t)

(1)

(3)对xi(t)分别进行EMD分解，得到J个IMF，记为cij(t)(j=1,2,…,J)，余项记为ri(t).其中，cij(t)表示第i次加入高斯白噪声后分解得到的第j个IMF.

(4)对步骤(3)中得到的IMF进行总体平均，得到EEMD分解后的IMF分量：

(2)

1.2IDMM趋势线

当转速恒定时，齿轮啮合信号时频谱中会出现相应的突出峰值，这些峰值的纵坐标所对应的数值为齿轮啮合频率及其倍频.其中幅值最大的突出峰对应的纵坐标与齿轮转频之间的比值是固定不变的，计算公式如式(3)所示:

(3)

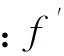
由式(3)可知，当齿轮以变转速工作模式运行时，峰值啮合倍频将以与转速相同的变化规律随时间发生改变.文献[7]将最大啮合倍频定义为IDMM.IDMM随时间变化所构成的集合为IDMM趋势线.由于齿轮振动信号在滚动轴承与齿轮的混合信号中具有幅值上的优势，所以IDMM趋势线容易从混合信号的时频图中直接提取.文中利用短时傅里叶变换(STFT)以及峰值搜索算法提取IDMM趋势线，计算公式如下：

STFT(t,ω)=∫-∞+∞g(u)f(t+u)e-jωudu

(4)

IDMMk=arg max{STFTk}

(5)

(k=1,2,…,K)

式中：t代表时间;ω为频率;f(t)表示原始振动信号；g(u)为高斯窗函数；STFTk代表瞬时频谱；k为瞬时频谱对应的序号,取值为1-K，K取决于原始信号与高斯窗函数的长度；arg max函数表示STFTk取得最大值时对应的时频域横坐标.

2基于EEMD和IDMM的滚动轴承故障诊断算法

滚动轴承振动信号为高频信号，齿轮啮合信号分布在低频，根据EEMD算法分解得到的IMF分量依据频率从高到低依次分布这一特性以及EEMD较EMD能减少模式混叠的优势，文中将其应用于去除齿轮噪声.IDMM趋势线在滚动轴承和齿轮混合信号中具有明显的幅值优势，便于提取.根据旋转部件中齿轮转频与轴承转频固定的比例关系可知，IDMM趋势线与轴承转频的变化规律是一致的，而且具有固定的比例系数，因此可以将其等效为轴承转频以减少辅助设备的安装成本以及安装空间对滚动轴承故障诊断的限制.需要指出的是文中算法仅适用于齿轮转频与轴承转频有固定比例关系的旋转部件，如齿轮箱.另外，文中选取峭度值最大的IMF分量作为滚动轴承振动信号进行后续分析.峭度是描述波形尖峰度的一个无量纲参数，它对信号的冲击成分非常敏感，即冲击成分比重越大，峭度值就越大，因此可以用峭度值衡量IMF分量中故障冲击成分的多少.峭度值可由公式(6)计算.

(6)

其中：E[·]表示数学期望，σ和μ分别表示数列x的标准差和均值.

文中方法的主要步骤如下：

(1)利用峰值搜索算法从原始信号的时频图中提取IDMM趋势线，将IDMM趋势线等效为轴承转频对原始信号进行重采样，得到角域重采样信号；

(2)采用EEMD算法对重采样信号进行分解，得到IMF分量之和；

(3)利用式(6)求取各IMF分量的峭度值，选取峭度值最大的IMF分量作为滚动轴承的振动信号；

(4)对选取的IMF分量进行包络谱分析，以确定滚动轴承的故障类型.

3仿真与实验分析

3.1仿真分析

为了验证文中方法消除变转速影响以及去除齿轮噪声的有效性，文中构造了变转速模式下包含齿轮噪声的滚动轴承故障混合信号.

变转速工作模式的滚动轴承故障信号xbearing的仿真公式[16]如式(7)所示：

(7)

式中：Am是由故障引起的第m个冲击的幅值；β表示结构衰减系数；ωr为由轴承故障引起的共振频率，u(t)为单位阶跃函数;tm为第m个冲击发生的时间，可由递推公式(8)确定：

(8)

变转速工作模式的健康齿轮振动信号的仿真公式如式(9)所示：

(9)

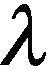
表1变转速条件下滚动轴承与齿轮混合信号仿真模型参数

Table 1Parameters of mixed bearing and gear simulation model under variable rotating speed

参数数值信号时长/s8采样频率fs/Hz20000故障特征系数3齿轮齿数L18结构衰减系数β800轴承共振频率ωr/Hz5000转频比1.2

仿真的变转速工作模式齿轮和故障轴承混合振动信号的表达式如式(10)所示：

xmix=xbearing+xgear+n(t)

(10)

式中,n(t)为高斯白噪声，信噪比为10 dB.

选取上述混合信号的最后1 s时长对文中方法进行验证.仿真混合信号的时域波形图如图1(a)所示，从图中可看出滚动轴承故障冲击不明显，被大量齿轮信号覆盖.利用峰值搜索算法从原始信号的时频图中得到的IDMM趋势线如图1(b)中的实线所示.图1(b)中点线代表预设的齿轮啮合频率，虚线代表2阶预设的齿轮啮合频率.2阶预设的齿轮啮合频率与提取的IDMM趋势线变化趋势相同，数值相差很小.

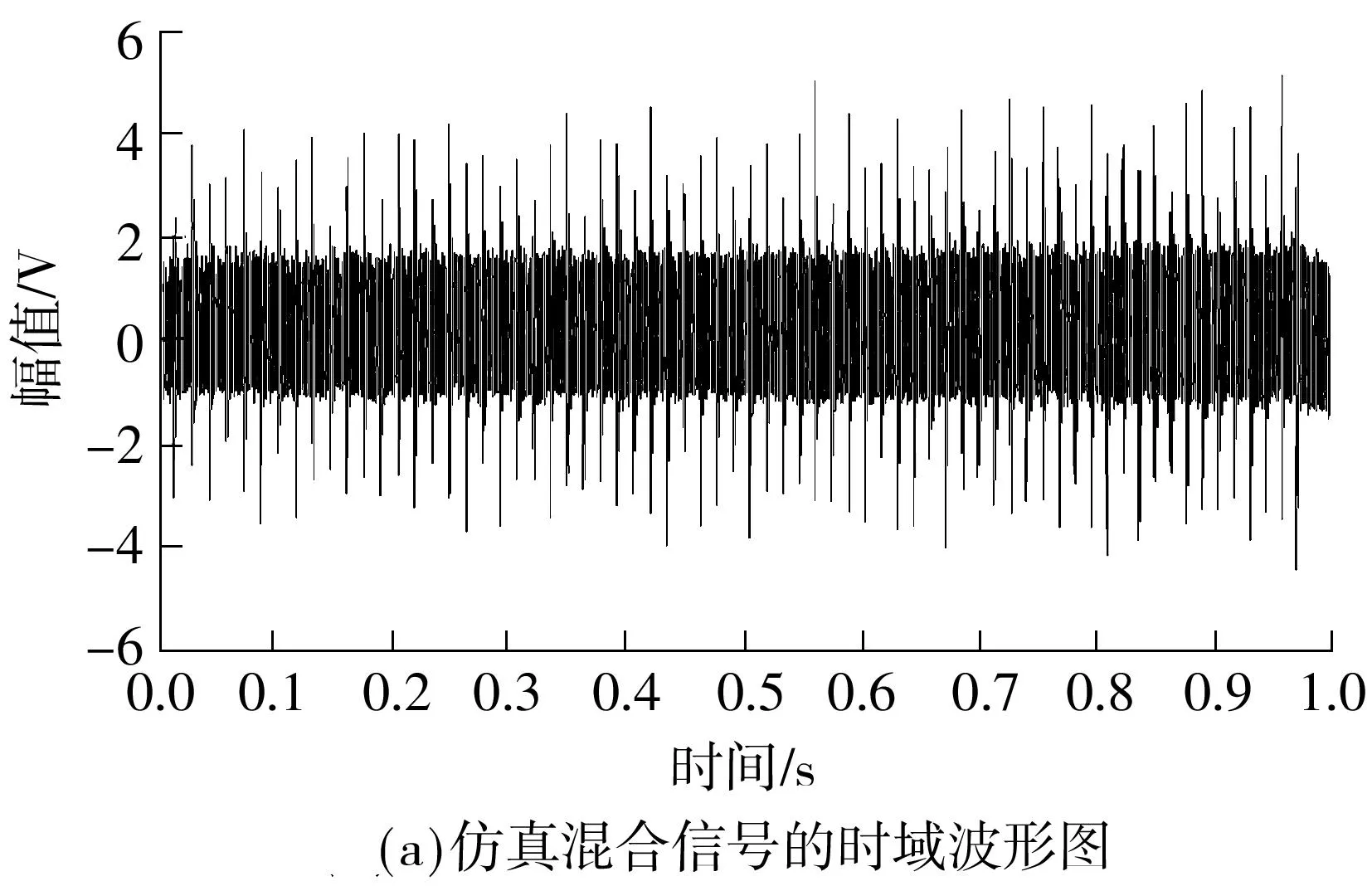
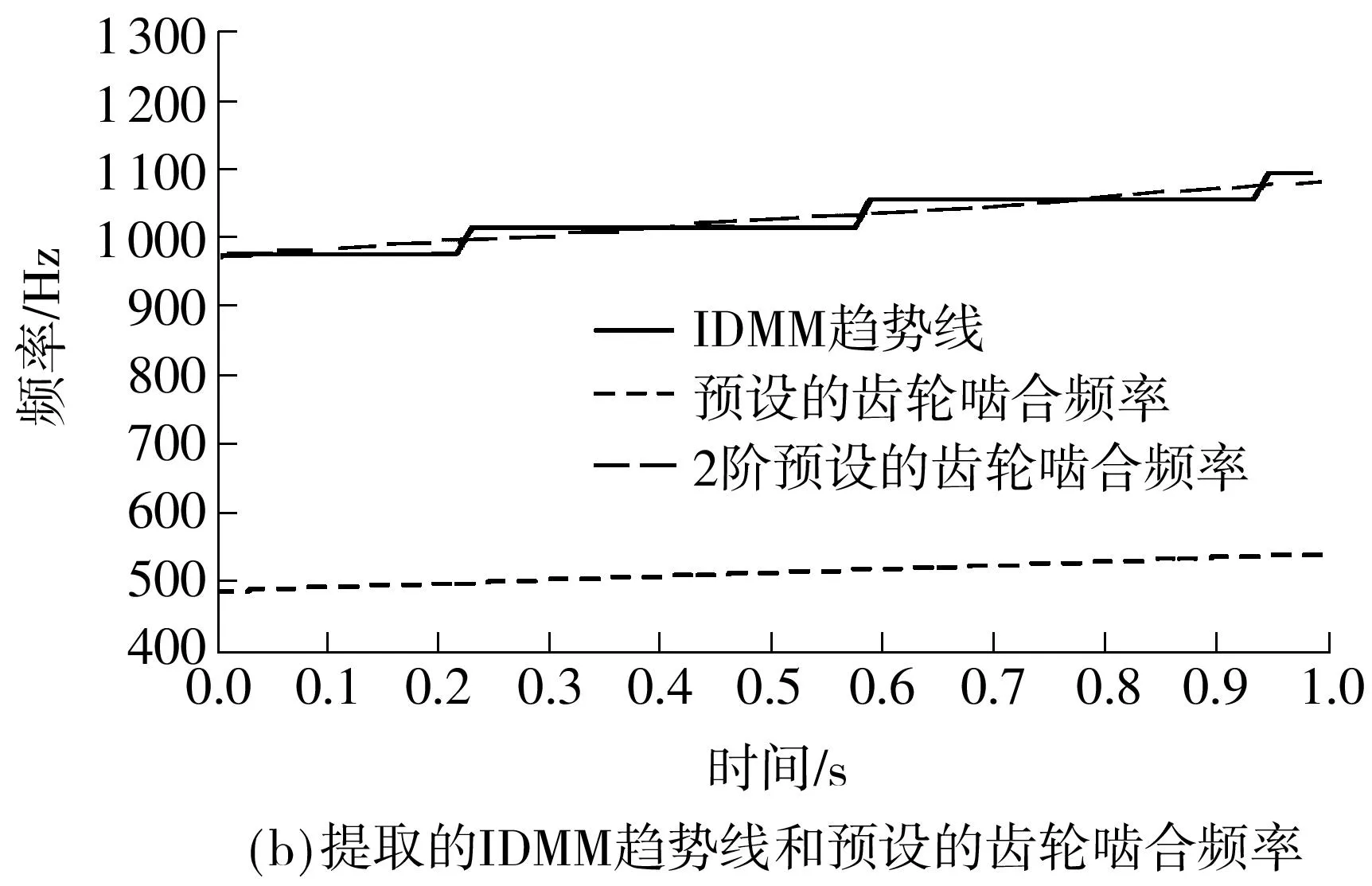
图1仿真混合信号的时域波形图及峰值搜索算法提取的IDMM趋势线和预设的齿轮啮合频率

Fig.1Mixed simulation signal in time domain，extracted IDMM trend by peak searching algorithm and preset gear instantaneous meshing frequency

根据IDMM趋势线对原始信号进行角域重采样，重采样信号如图2(a)所示.利用EEMD算法对重采样信号进行分解，得到10个IMF分量，图2(b)给出了前6个分量.从图2(b)中可以看到IMF2故障冲击十分明显.分别求取各个IMF分量的峭度值.前6个IMF分量的峭度值分别为3.18、15.41、1.91、2.96、2.83和2.53.其中IMF2的峭度值为最大，选取IMF2进行分析.分别对IMF2和重采样信号进行包络谱分析，得到包络谱分别如图3(a)、3(b)所示.

由图3(a)可以明显地看到轴承转频阶比及其二倍谐波(横坐标分别为0.023 13和0.046 25)，以及故障特征阶比及其二、三倍谐波，(横坐标分别为0.069 38、0.138 8和0.208 7).计算出故障特征系数

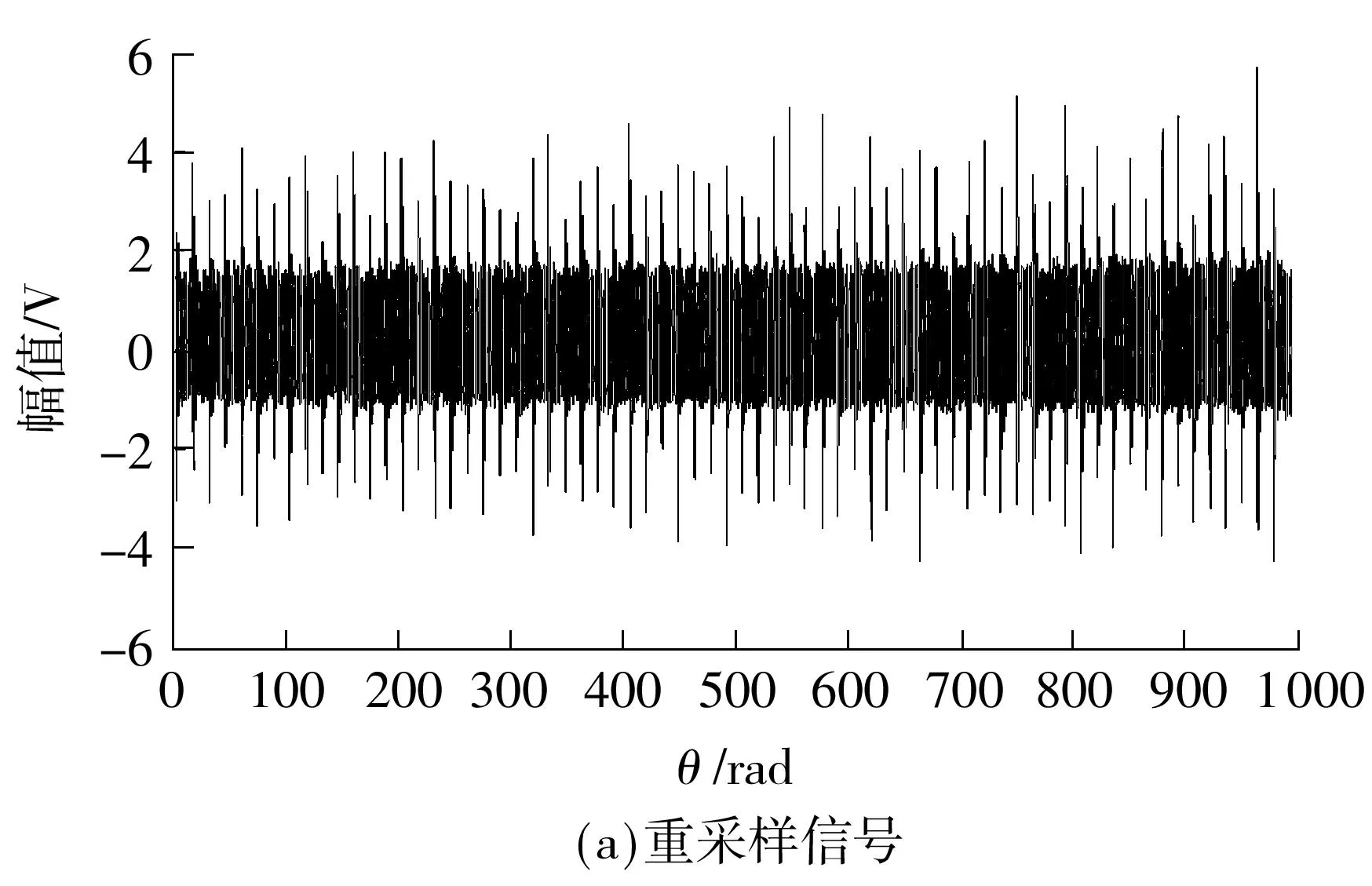
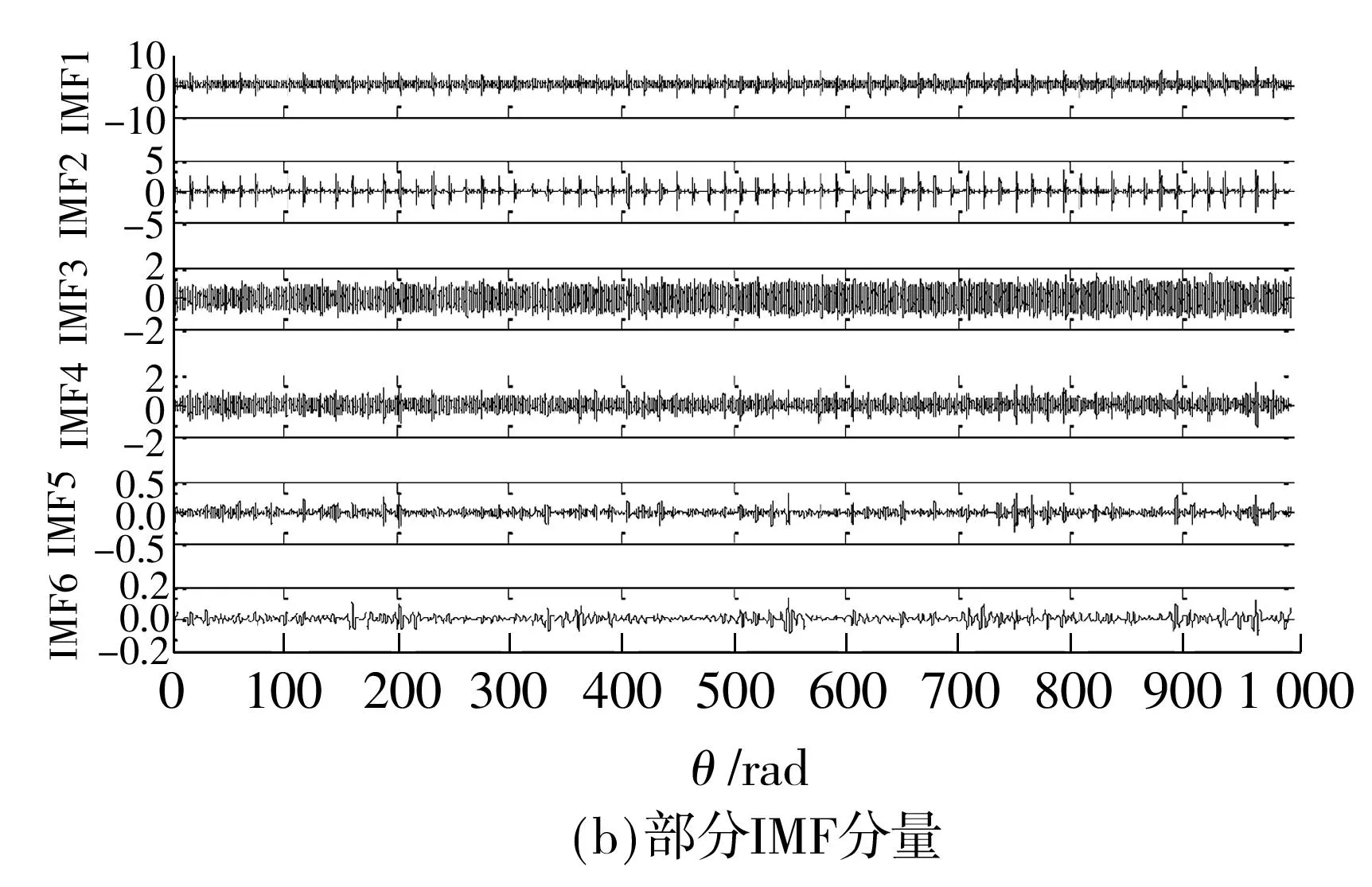
图2　重采样信号及部分IMF分量

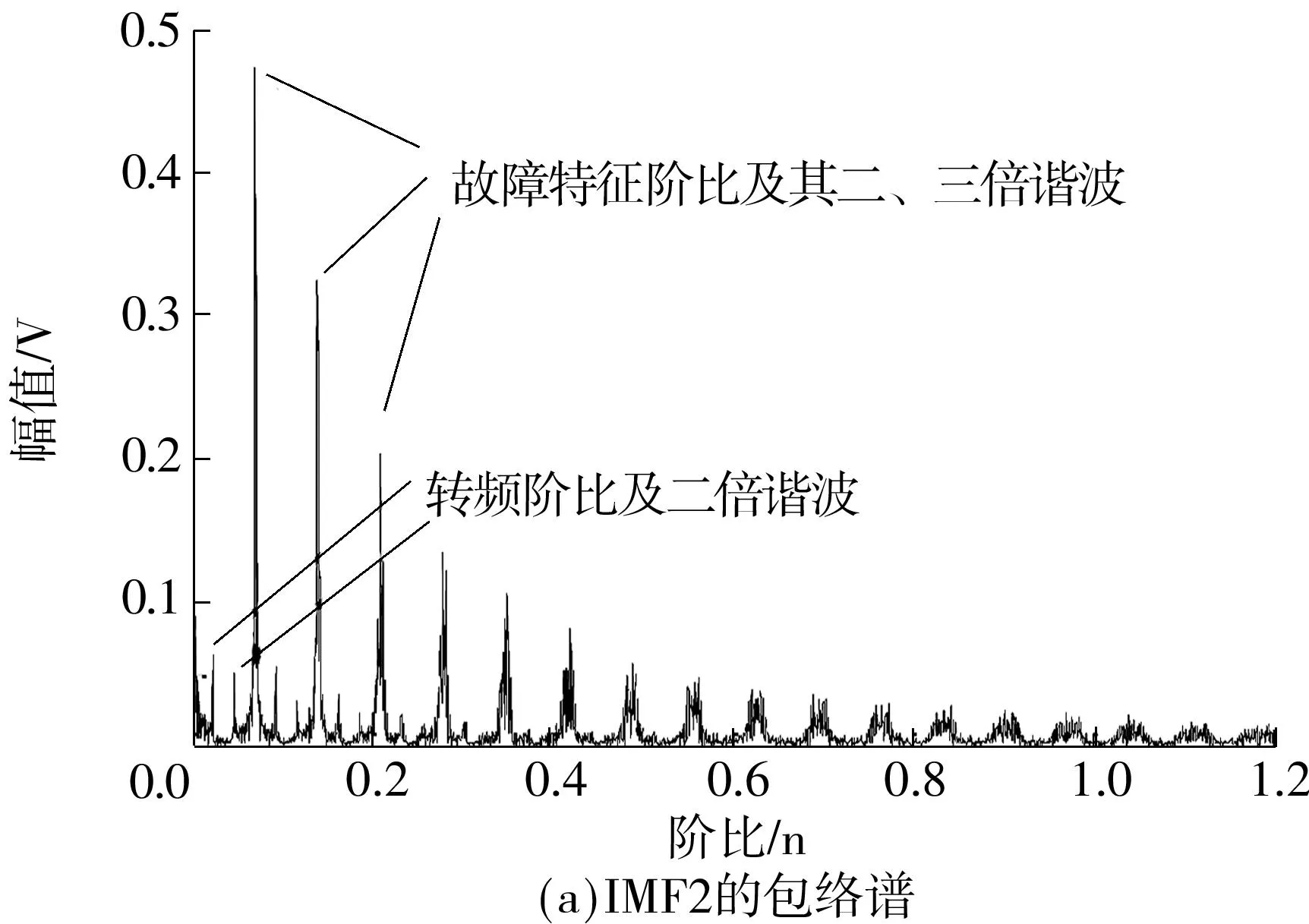
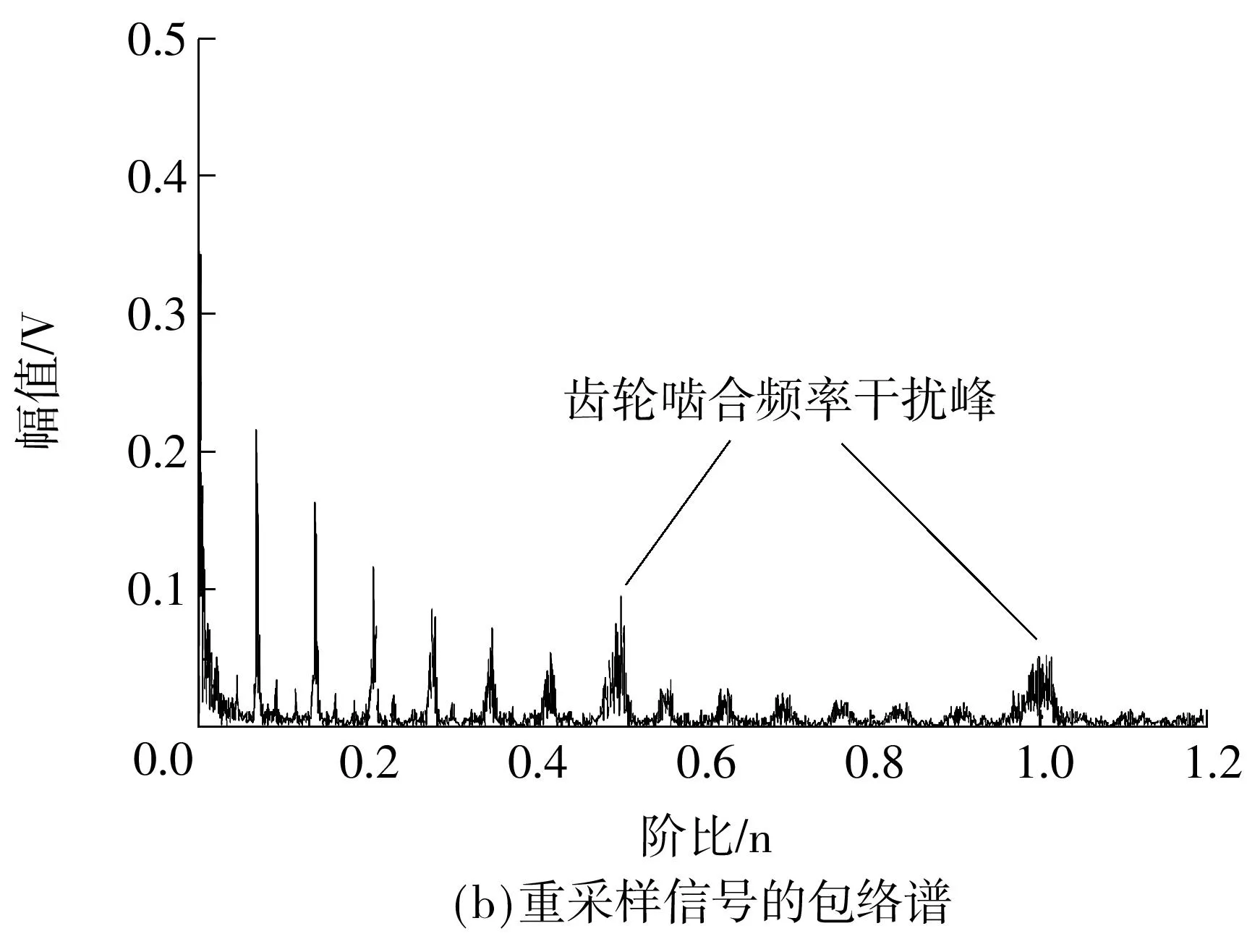
图3　IMF2的包络谱及重采样信号的包络谱

Fig.3Envelope order spectra of IMF2 and the resampled signal

为2.999 6，理论值为3，从而说明文中方法能有效确定滚动轴承的故障类型.

图3(b)给出了重采样信号的包络谱，图中有明显的齿轮干扰成分，低频阶段由于受齿轮啮合频率干扰，轴承转频峰值被淹没在噪声中.通过图3(a)、3(b)两图的比对可以看出，基于EEMD和IDMM的滚动轴故障诊断方法可以有效去除齿轮噪声干扰，同时大幅提升故障特征阶比及其谐波的幅值.

3.2实验验证

利用滚动轴承振动试验台上的实测信号验证文中方法的有效性.图4为能够产生齿轮以及滚动轴承混合信号的实验装置.其中，速度调节器调节电动机转速，电机通过联轴器与齿轮箱相连.传感器安置在故障轴承附近以准确测取其振动信号.齿轮箱为直齿单级传动，传动比为3/11，主动轮齿数为55.以电火花切割凹坑模拟外圈点蚀故障的滚动轴承位于齿轮箱输入端，滚动轴承型号为6 206，根据滚动轴承的几何参数计算该轴承外圈故障特征系数[2,7]为3.66.在齿轮箱的输出轴端安装转速计测取齿轮的转速信息.

图4　试验台

实验过程中电机转速逐渐增加，采样率设为24 kHz，截取其中1.5 s时长进行分析.采集的混合振动信号如图5(a)所示.利用峰值搜索算法从原始信号的时频图中提取的IDMM趋势线(实线)如图5(b)所示.另外，实测的齿轮啮合频率为点线，其2倍频为虚线.由图5(b)中各曲线对比可知利用峰值搜索算法提取的IDMM趋势线与实测的齿轮啮合频率的变化趋势相同，数值与齿轮啮合频率2倍频的数值相接近，因此可以将IDMM趋势线等效为轴承的转频.

根据提取的IDMM趋势线，获得的重采样信号如图6所示.对重采样信号进行EEMD分解，得到13个IMF分量，求得的前6个IMF分量的峭度值分别为3.09、21.18、3.15、3.59、2.56和2.53.其中IMF2的峭度值为21.18，数值最大，因此选取IMF2进行分析.

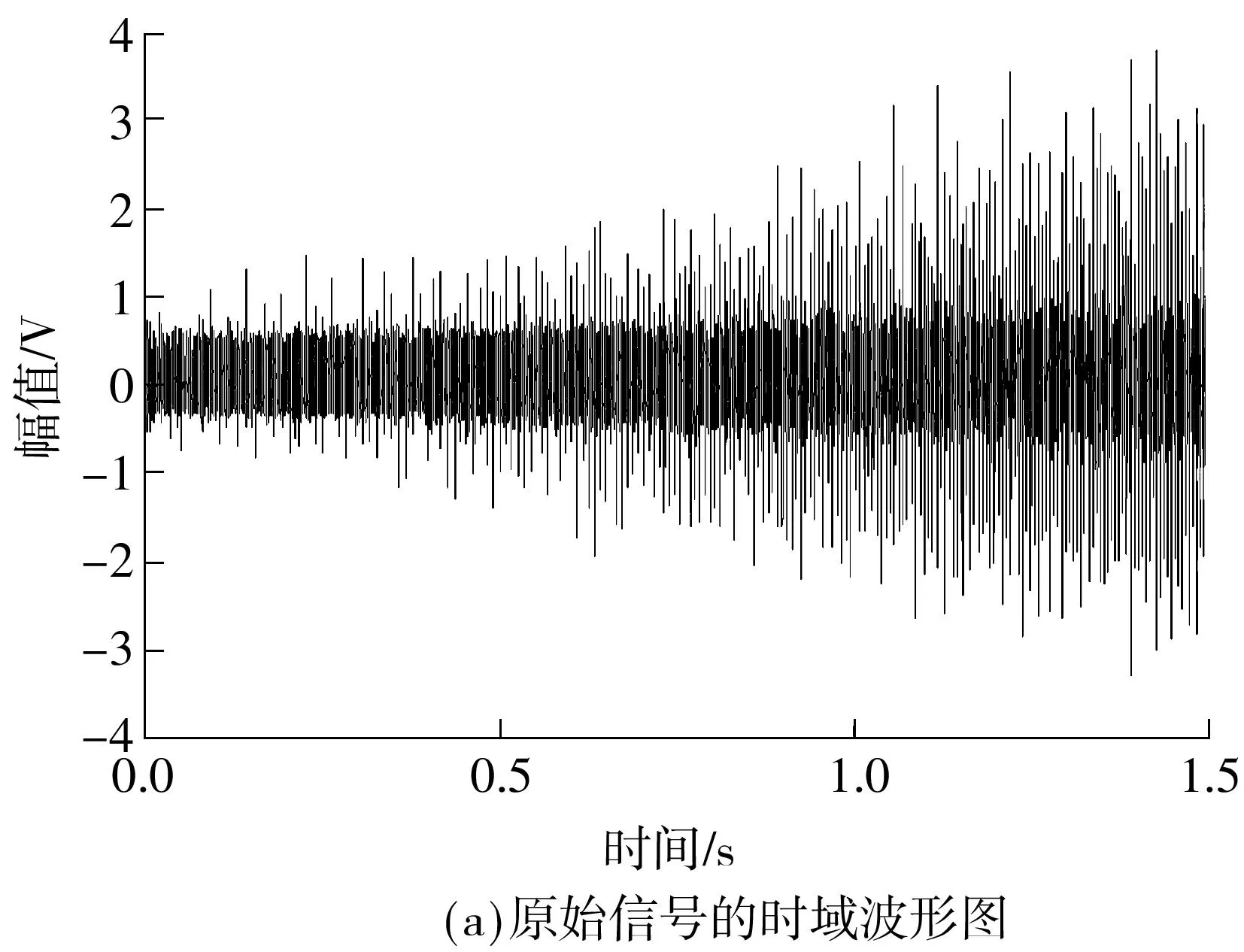
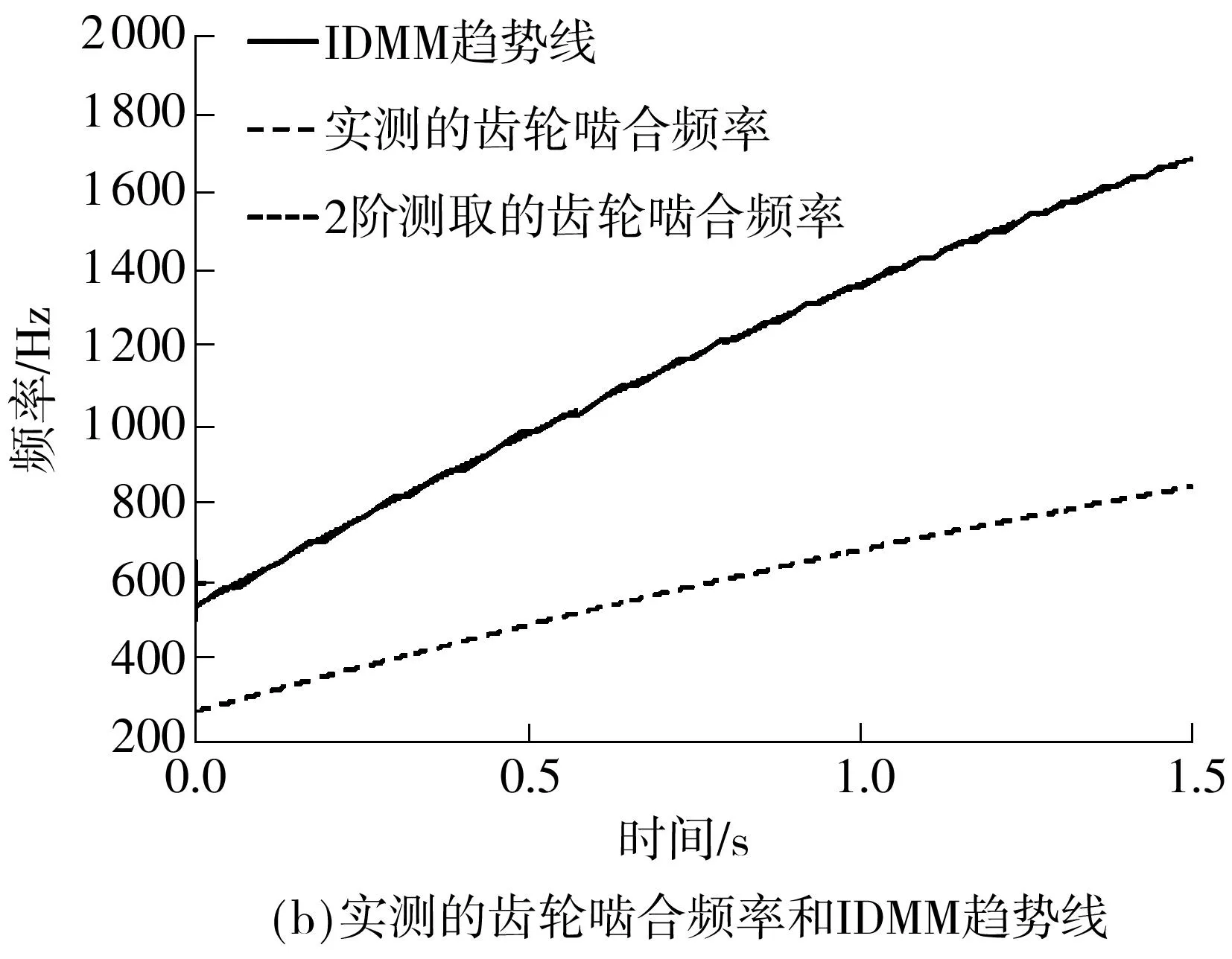
图5原始信号的时域波形图以及实测的齿轮啮合频率和IDMM趋势线

Fig.5Mixed signal in time domain，extracted IDMM trend and measured gear instantaneous meshing frequency

图6　验证试验中的重采样信号

对IMF2进行包络谱分析，得到包络谱如图7(a)，与图7(b)(重采样信号的包络谱)相比，齿轮啮合频率干扰峰被去除，故障特征阶比峰值的幅度也明显增加.图7(a)中一阶转频阶比峰值对应的横坐标为0.032 34，一阶故障特征阶比为0.117 5，两个数值的比值为3.63，而滚动轴承实际故障特征系数为3.66，因此可以确定该轴承外圈出现故障.

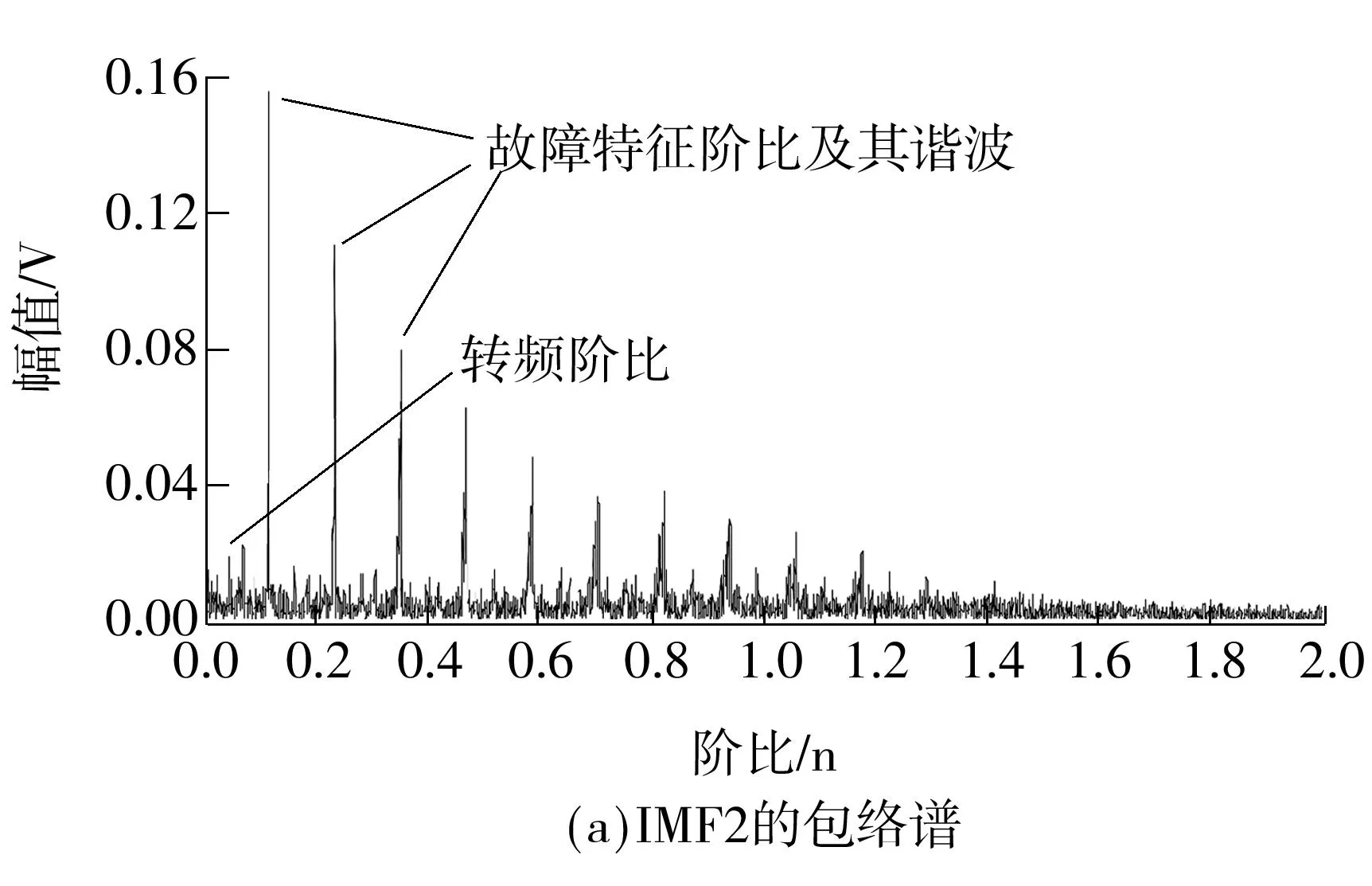
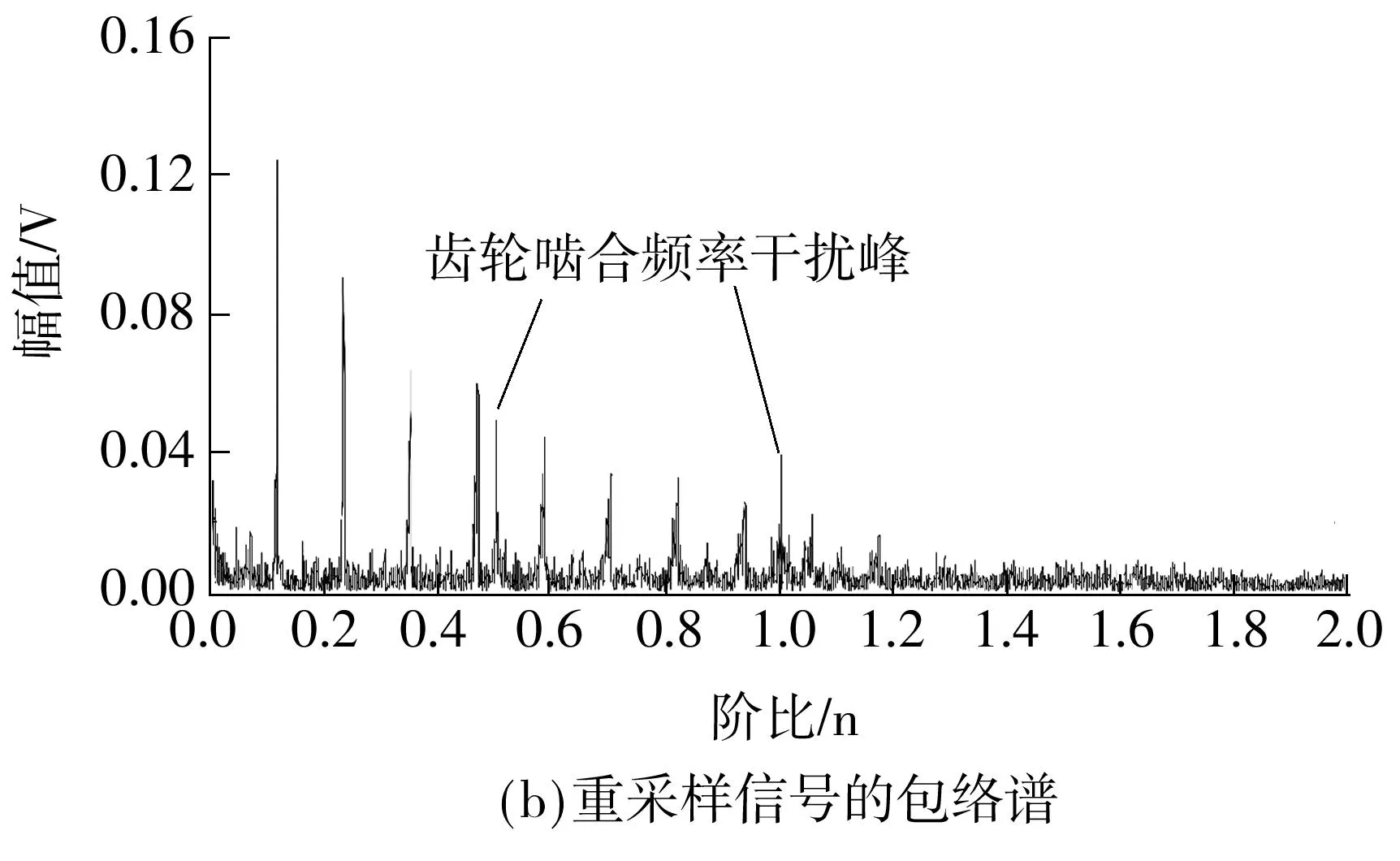
图7　验证试验中IMF2的包络谱及重采样信号的包络谱

Fig.7Envelope order spectra of IMF2 and the resampled signal in verification test

4结论

(1)将EEMD算法用于滚动轴承的故障诊断，能有效去除混合信号中的齿轮噪声干扰成分，利用IDMM易于提取以及IDMM趋势线与轴承转频存在固定的比例系数等特性，将其等效为轴承转频，减少了滚动轴承故障诊断过程对转速计等辅助设备的依赖.

(2)基于EEMD和IDMM的滚动轴承故障诊断方法可以有效地判断轴承是否发生故障以及故障类型，相对于重采样信号的包络谱，文中方法获得的包络谱中轴承故障特征阶比幅值以及转频阶比幅值明显提高.

参考文献：

[1]CHENG W D，GAO R X，WANG J J，et al.Envelope deformation in computed order tracking and error in order analysis [J].Mechanical System And Signal Processing，2014，48(1/2):92- 102.

[2]GUO Y，LIU T W，NA J，et al.Envelope order tracking for fault detection in rolling element bearings [J].Journal of Sound and Vibration,2012,331(25):5644- 5654.

[3]SAAVEDRA P N，RODRIGUEZ C G.Accurate assessment of computed order tracking [J].Shock and Vibration，2006，13(1):13- 21.

[4]WANG K S，HEYNS P S.The combined use of order tracking techniques for enhanced Fourier analysis of order components [J].Mechanical Systems and Signal Processing，2011，25(3):803- 811.

[5]COATS M D，RANDALL R B.Order-tracking with and without a tacho signal for gear fault diagnostics [C]∥Proceedings of Acoustics.Fremantle:[s.n.]，2012：1- 8.

[6]赵晓平，赵秀莉，侯荣涛，等.一种新的旋转机械升降速阶段振动信号的瞬时频率估计算法 [J].机械工程学报,2011，47 (7):103- 108.ZHAO Xiao-ping，ZHAO Xiu-li，HOU Rong-tao，et al.A new method for instantaneous frequency estimation of run-up or run-down vibration signal for rotating machinery [J].Journal of Mechanical Engineering，2011，47(7):103- 108.

[7]WANG T Y，LING M，LI J Y，et al.Bearing fault diagnosis under unknown variable speed via gear noise cancellation and rotational order side band identification [J].Mechanical System and Signal Processing，2015，62/63:30- 53.

[8]HUANG N E，SHEN Z，LONG S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J].Proceedings of the Royal Society of London Series A-Mathematical Physical and Engineering Sciences，1998，454:903- 995.

[9]RATO R T，ORTIGUEIRA M D，BATISTA A G.On the HHT，its problems，and some solutions [J].Mechanical Systems and Signal Processing，2008,22(6):1374- 1394．

[10]GAI G H.The processing of rotor startup signals based on empirical mode decomposition [J].Mechanical Systems and Signal Processing，2006，20(1):225- 235．

[11]WU Z，HUANG N E.Ensemble empirical mode decomposition:a noise assisted data analysis method [J].Advances in Adaptive Data Analysis，2009，1(1):1- 41.

[12]彭畅,柏林,谢小亮.基于 EEMD、度量因子和快速谱峭度图的滚动轴承故障诊断方法 [J].振动与冲击，2012,31(20):143- 146.

PENG Chang，BO Lin，XIE Xiao-liang.Fault diagnosis method of rolling element bearing based on EEMD，measure-factor and fast kurtogram [J].Journal of Vibration and Shock,2012,31(20):143- 146.

[13]曹冲锋,杨世锡,杨将新.大型旋转机械非平稳振动信号的EEMD降噪方法 [J].振动与冲击,2009,28(9):33- 38．

CAO Chong-feng，YANG Shi-xi，YANG Jiang-xin.De-noising method based on EEMD for large rotating machinery vibration signal [J].Journal of Vibration and Shock，2009,28(9):33- 38．

[14]李昌林,孔凡让,黄伟国,等.基于EEMD和Laplace小波的滚动轴承故障诊断 [J].振动与冲击,2014,33(3):63- 69.

LI Chang-lin，KONG Fan-rang，HUANG Wei-guo，et al.Rolling bearing fault diagnosis based on EEMD and Laplace wavelet [J].Journal of Vibration and Shock，2014,33(3):63- 69.

[15]唐贵基,王晓龙.基于EEMD降噪和1.5维能量谱的滚动轴承故障诊断研究 [J].振动与冲击,2014,33(1):6- 10.

TANG Gui-ji，WANG Xiao-long.Fault diagnosis for roller bearings based on EEMD de-noising and 1.5-dimensional energy spectrum [J].Journal of Vibration and Shock，2014，33(1):6- 10.

[16]王天杨,李建勇,程卫东.基于改进的自适应噪声消除和故障特征阶比谱的齿轮噪源干扰下变转速滚动轴承故障诊断 [J].振动与冲击,2014,33(18):7- 13.

WANG Tian-yang，LI Jian-yong，CHENG Wei-dong.Fault diagnosis of rolling bearing under a variable rotational speed and gear vibration noise based on revised ANC algorithm and FCO spectrum [J].Journal of Vibration and Shock，2014，33 (18):7- 13.

Fault Diagnosis of Rolling Bearing Under Gear Noise Interference and Variable Rotating Speed

ZHAODe-zunLIjian-yongCHENGWei-dong

(School of Mechanical Electronic and Control Engineering, Beijng Jiaotong University, Beijing 100044, China)

Abstract:In order to improve the fault diagnosis accuracy of rolling bearings that are commonly interfered by gear noise and variable rotating speed, a fault diagnosis method based on the ensemble empirical mode decomposition (EEMD) and the instantaneous dominant meshing Multiply(IDMM) is proposed. The proposed method employs EEMD to eliminate the gear noise in bearing vibration signals, transfers IDMM into an instantaneous rotating frequency, and uses the order tracking to overcome the decrease of diagnosis accuracy due to rotating speed variation. Simulated and experimental results show that the proposed method is effective in eliminating the interferences caused by gear noise and rotating speed variation, thus improving the characteristic order amplitude of faults. Accordingly, the installation of tachometers can be avoided.

Key words:variable rotating speed; gear noise; rolling bearing;fault diagnosis; ensemble empirical mode decomposition; instantaneous dominant meshing multiply

doi：10.3969/j.issn.1000-565X.2016.02.011

中图分类号：TH 113.1

文章编号:1000- 565X(2016)02- 0067- 07

作者简介:赵德尊(1990-)，男，博士生，主要从事制造装备智能测控与故障诊断研究.E-mail:14116346@bjtu.edu.cn†通信作者: 程卫东(1967-)，男，副教授，主要从事制造装备智能测控与故障诊断教学与研究.E-mail:wdcheng@bjtu.edu.cn

*基金项目:国家自然科学基金资助项目(51275030)

收稿日期:2015- 06- 19

Foundation item: Supported by the National Natural Science Foundation of China(51275030)