固体潮对测站位移的影响特征分析

王　伟,章传银,杨　强,柯宝贵

(中国测绘科学研究院，北京 100830)



固体潮对测站位移的影响特征分析

王伟,章传银,杨强,柯宝贵

(中国测绘科学研究院，北京 100830)

Analysis of Solid Earth Tides Effects on Station Displacements

WANG Wei,ZHANG Chuanyin,YANG Qiang,KE Baogui

摘要：采用IERS规范上的方法和2013年发布的DE430星历文件，计算并分析了北京房山站和浙江地区固体潮对测站位移的影响。研究发现，固体潮影响具有很强的周期性，存在2周和半年的长周期，在局部区域的等值线都成线状分布。本文研究可为固体潮方面的相关研究提供参考。

关键词：固体潮；位移影响；特征分析

在引潮力作用下，地球内部和外部形状时刻发生着周期性变化，通常将这种现象称为地球固体潮[1]。固体潮对重力、应变和地表位移等地球物理场产生影响，因此，现代空间大地测量观测必须考虑固体潮的影响。固体潮对地面测站位移的影响是指引潮位导致粘弹性地球形变，引起对地面站点位移的间接影响。

在空间大地测量数据处理中，固体潮影响的公式逐渐趋于IERS标准[2]。固体潮对位移影响的研究有计算引潮力位与地球形变之间关系的固体潮勒夫数、精化时间域内二阶和三阶引潮力位对位移影响的公式、不同固体潮模型改正的差异等[3-7]。而针对固体潮影响的特征分析较少。

本文主要是采用IERS2010规范上的方法[8]，采用更新的星历文件DE430，计算固体潮对测站位移的影响，并对该影响进行时频分析，揭示在WGS-84坐标系下X、Y、Z3个方向上的特征和规律。

一、固体潮影响的计算

为顾及纬度的相关性，IERS协议采用Mathews理论[9]的位移勒夫数多重表达方式，给出了分潮引起的地面测站位移的向量表达式。

固体潮对测站位移的影响通常分两步计算：

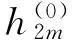
2) 考虑频率相关的二阶位移勒夫数与标称值的偏差，对第1步的计算结果进行改正，改正包括周日位移勒夫数虚部的贡献。

地面测站位移固体潮的间接影响等于第1步和第2步计算结果之和[8]。

采用美国宇航局(NASA)喷气推进实验室(JPL)发布的DE430星历文件计算日、月位置。DE430星历发布于2013年，可以计算从1550年1月1日至2650年1月22日间的行星位置，含有目前精度最高的月球星历。DE430星历文件可以在JPL服务器ftp:∥ssd.jpl.nasa.gov/pub/eph下载。

二、数据分析

本文选择了浙江地区的部分测站进行固体潮影响研究，研究区域和测站如图1所示。

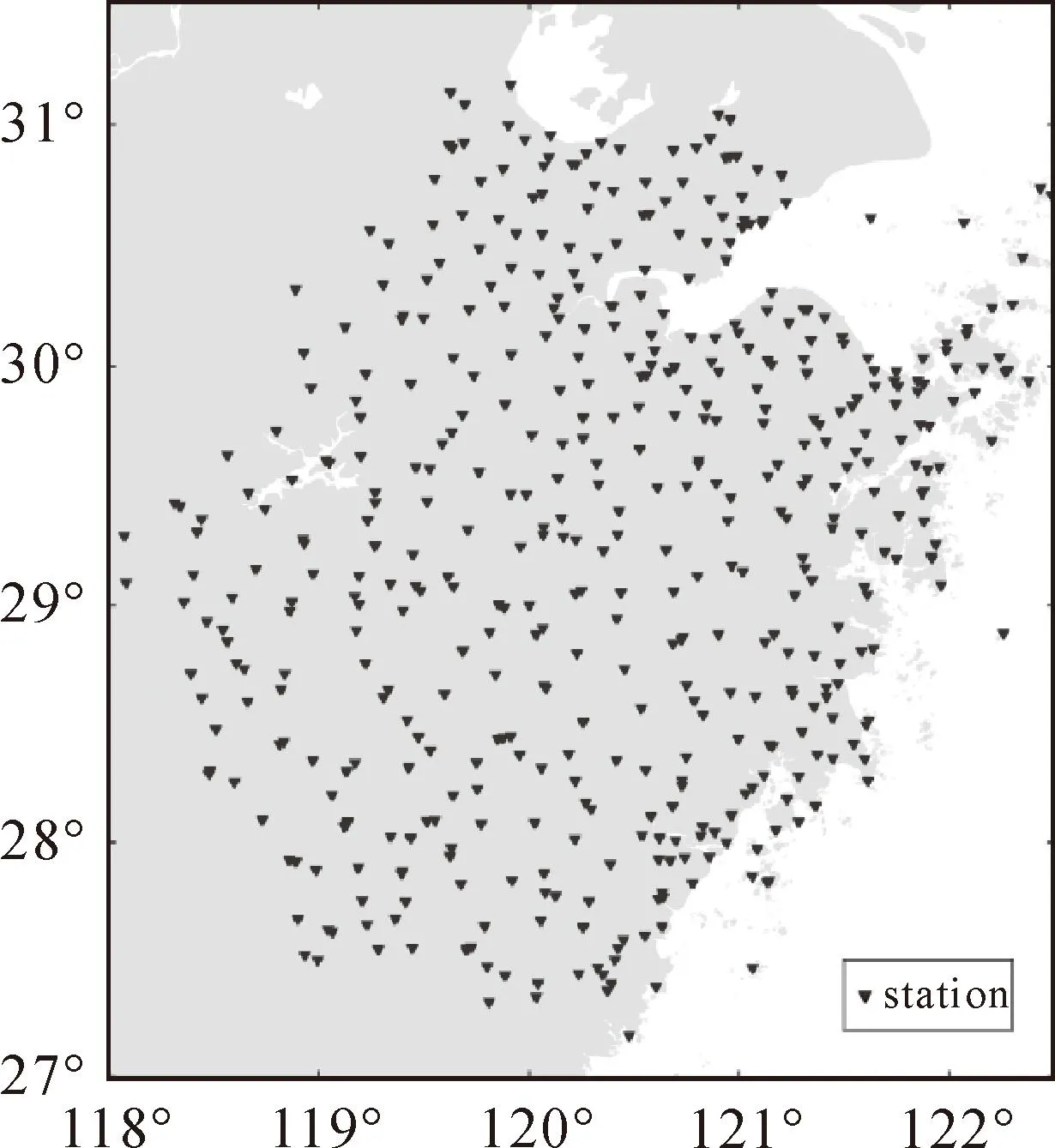
图1　研究区域及测站位置

根据IERS2010规范中的方法，采用DE430星历计算固体潮对测站位移影响。计算北京房山站2012年1—2月两个月的固体潮影响情况，如图2所示。

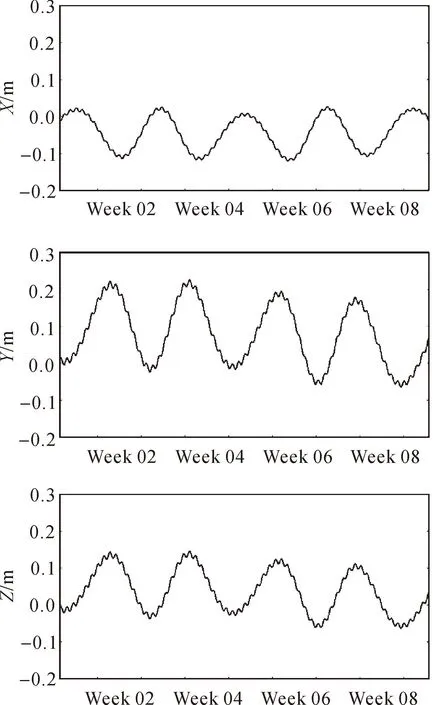
图2　房山站2012年1—2月的固体潮影响

从图2可以发现，固体潮在试验的两个月内，呈现明显的周期性，周期约2周。在X方向上的最大值与在Y和Z方向上的最小值接近，都在0左右。在Y方向上的最大值在0.2 m左右。Y与Z方向上的波形相似，且都与X方向波形相反。

为进一步研究固体潮影响的特征，扩大研究时间跨度，计算北京房山站从2012年1月1日至2014年12月31日的固体潮影响，如图3所示。

由图3可以发现，固体潮的影响在长时间跨度上同样有很强的周期性，存在约半年的周期。在Y方向上同样存在3个方向上的最大值。Y与Z方向上影响值的波形相似，与X方向上的波形相反。

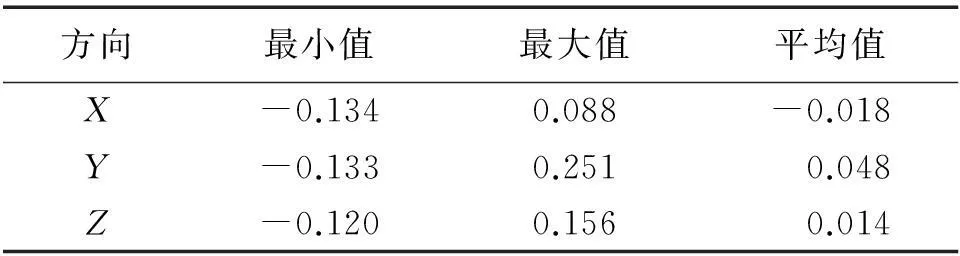
将固体潮影响在WGS-84坐标系下3个方向上的值进行统计，见表1。3个方向上的最小值接近，最大值相差较大，Y方向上较其他两个方向最大值偏大。

为了研究固体潮影响的区域特点，分别计算研究区域多个时间点上的固体潮影响。通过多次试验计算可知：在局部区域，固体潮影响在X、Y和Z3个方向上的等值线都成线状分布；Y方向上的影响值较X和Z方向上偏大，与之前的时间序列分析一致。图4、图5分别是2015年2月3日0点和4月3日0点固体潮影响在X、Y、Z3个方向上的等值线图。

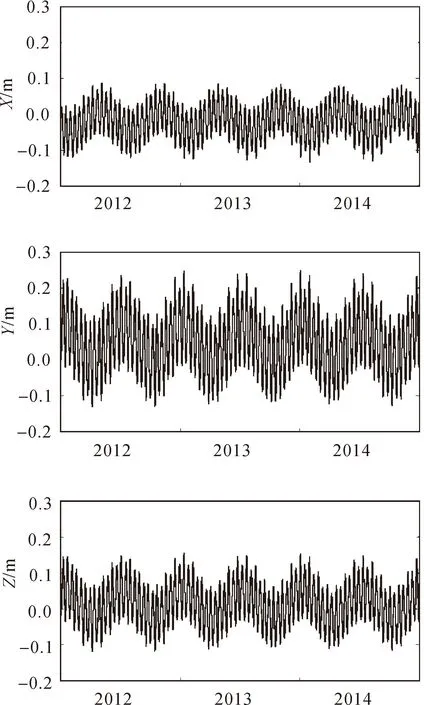
图3　房山站2012—2014年的固体潮影响

m

三、结束语

本文计算了房山站和局部区域的固体潮影响，分析了固体潮影响的特征。固体潮对测站位移的影响呈现明显的周期性，存在2周和半年的长周期特征。同一测站上Y和Z方向上的固体潮影响波形相似，Y方向上的影响值较X和Z方向上偏大。在局部区域，固体潮影响在3个方向上的等值线都成线状分布。本文研究结果可以为固体潮方面的相关研究提供参考。

图4　研究区域固体潮影响等值线图(2015年2月3日)

图5　研究区域固体潮影响等值线图(2015年4月3日)

参考文献：

[1]孙和平,许厚泽,陈武,等.香港地区重力固体潮和海潮负荷特征研究[J].地球物理学报,2006(3): 724-734.

[2]张捍卫,郑勇,赵方权.固体潮对测站位移影响的理论研究[J].大地测量与地球动力学,2003(3): 98-103.

[3]JOHN M G. Test of Theoretical Solid Earth and Ocean Gravity Tides[J].Geophysical Journal International, 1996(1): 106-114.

[4]董春来,路长城,郭淑艳,等. 海潮对GNSS高精度测量影响的研究[J].测绘通报,2011(2):4-5,20.

[5]ZAHRAN K H, JENTZSCH G, SEEBER G. World-wide Synthetic Tide Parameters for Gravity and Vertical and Horizontal Displacements[J]. Journal of Geodesy,2005 (6-7):293-299.

[6]殷海涛,李杰,马丕峰,等.固体潮模型对GPS时间序列的影响研究[J].大地测量与地球动力学,2009(2): 48-52.

[7]王文利,陈士银,董鸿闻. 现行水准测量日月引力改正数学模型的分析与使用[J].测绘通报,2000(12): 8-9.

[8]GÉRARD P， BRIAN L. IERS Conventions (2010) [M]. Frankfurt am Main: Verlag des Bundesamts für Kartographie und Geodäsie, 2010.

[9]MATHEWS P M, BUFFETT B A, SHAPIRO I I. Love Numbers for a Rotating Spheroidal Earth: New Definitions and Numerical Values[J]. Geophysical Research Letters, 1995 (5):579-582.

[10]CARTWRIGHT D E, TAYLER R J. New Computations of the Tide-generating Potential[J]. Geophysical Journal of the Royal Astronomical Society, 1971 (1):45-74.

中图分类号：P229

文献标识码：B

文章编号：0494-0911(2016)03-0007-03

通信作者：章传银

作者简介：王伟(1981—)，男，博士，副研究员，主要从事物理大地测量和卫星重力学等方面的研究工作。E-mail: wangwei@casm.ac.cn

基金项目：国家自然科学基金(413040019；41374081)

收稿日期：2015-04-16； 修回日期： 2015-11-06

引文格式： 王伟,章传银,杨强,等. 固体潮对测站位移的影响特征分析[J].测绘通报，2016(3)：7-9.DOI:10.13474/j.cnki.11-2246.2016.0073.