精密水准测量中固体潮改正的应用

2022-08-08王文利郭春喜秦世民

测绘工程 2022年4期

王文利，郭春喜，张涛，秦世民

(自然资源部大地测量数据处理中心，西安 710054)

月球、太阳等天体对地球存在着引力，这种引力称为引潮力[1]。由于引潮力的作用，固体地球测站上引力方向会变化，地面产生周期性的起伏，地壳内部密度也发生变化产生附加位，被称为固体潮[2]。固体潮对精密水准测量结果产生影响，它使水准仪垂线产生偏离，使前、后视读数产生误差，进而影响水准测量高差[1]。同时，引潮力使作为水准测量基准的水准面发生倾斜，进而影响水准测量的精度[3]。据研究统计，固体潮改正对水准环闭合差影响不太明显，一般均在2 mm以内[4-6]，但对于南北方向的水准路线而言，这项改正随距离而积累[7-8]。为此，在精密水准测量数据处理时，高差需加入固体潮改正，有效保证水准测量的精度。GB/T 12897-2006《国家一、二等水准测量规范》(简称《规范》)也明确规定：水准高差应加入固体潮改正[9]。目前精密水准测量数据一般只记录测段(两水准点间)往测、返测的始、末时间，《规范》中对精密水准测量的固体潮改正均是事后在数据处理中根据测段往、返测的始、末时间进行改正。因引潮力在不同地点、不同时刻都不相同(每日每时每刻在变化)，即使在相同地点、不同时刻都是变化的，而往测或返测的测段长度约为2～10 km，往测或返测的始末时间有同天、跨天、跨月甚至还有跨年的，所以，在事后数据处理时用测段往、返测的始、末时间计算固体潮改正，既要综合考虑同天上、下午观测，跨天、跨月、跨年观测时间，还要考虑各地太阳中天前后2 h不宜观测等因素，合理取用计算测段固体潮改正的观测时间(年、月、日、时、分)，达到准确地扣除固体潮影响的效果。但《规范》中测段高差固体潮改正计算，存在计算模型不详细、观测时刻取用不明晰，导致给用户带来计算结果差异较大、残存误差较大等问题，直接影响改正效果。在研究、分析的基础上，通过实例计算与长期数据处理经验，分析固体潮改正的变化规律，归纳整理出在精密水准测量数据处理中测段高差固体潮改正的详细计算模型、计算方法、观测时间(年、月、日、时、分)取用原则，并分析比较基于测站和测段的精密水准固体潮改正差异及测段高差固体潮改正方法的弊端，对今后精密水准测量中固体潮改正方法提出新思路与建议。

1 固体潮改正数学模型

精密水准测量测段高差的固体潮改正计算详细模型如下。

1)水准测量一测段高差的固体潮改正U算式为：

U=γ·[θmcos(Am-A)+θscos(As-A)]·Rs.

(1)

式中：γ为潮汐因子(γ=0.68)；θm,θs分别为月球、太阳在测站与天体方向的地倾斜影响,rad；Am,As分别为测站至月球、太阳方向的方位角(0°～360°);A为观测路线方向方位角(0°～360°)；Rs为测段距离,km。

2)月球、太阳的地倾斜影响θm,θs算式为[10]：

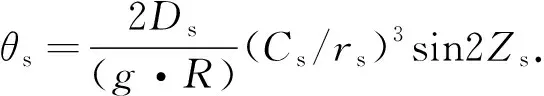
(2)

式中：g为地球平均重力值(g=982.0 cm/s2)；R为地球平均曲率半径(R=637 100 000 cm)；Dm,Ds分别为月球、太阳的杜德森常数，取值Dm=26 277.236 cm2/sec2,Ds=0.459 9Dm；Cm为地心至月球的平均距离(Cm=3.844×1010cm)；rm，rs分别为地心至月球、地心至太阳在观测时刻的瞬时距离；Zm，Zs分别为月球、太阳的天顶距(0°～180°)。

3)月地、日地的平均距离与瞬时距离比分别为Cm/rm，Cs/rs，真黄经λm，λs，真黄纬βm，βs算式为

(3)

式中：S为月球平黄经(°)；P为月球近地点平黄经(°)；H为太阳平黄经(°)，Ps为太阳近地点平黄经(°)；N为升交点平黄经(°)。

4)天文参数S,H,P,N,Ps算式为[11]：

(4)

式中：T为儒略世纪数。

5)儒略世纪数T算式为[12]：

T={[367y-int(7(y+int((m+9)/12))/4)+d+

(h-8)/24+int(275m/9)]-694 006.5}/36 525.

(5)

式中：y为年(公元);m为月;d为日;h为时(北京时);int为取整。

6)月球、太阳的赤纬与时角算式为[13]：

(6)

式中：ε为黄赤交角(°)，τ0为地方恒星时(°),δm,tm为日球的赤纬和时角，ts为太阳赤纬和时角。

7)黄赤交角ε、地方恒星时τ0计算：

ε=23.452 29°-0.013 01°·T-

0.000 002°·T2+0.000 000 5°·T3,

τ0=H+L+15(h-8)-180°.

(7)

式中：L为测段两端点的大地经度平均值；T为儒略世纪数；h为时(北京时)。

8)平均地心纬度φ、天体天顶距、天体方位角和水准路线方位角A算式为：

(8)

式中：AT，ZT分别表示月球和太阳的天体方位角及天体天顶距；B1,B2和L1,L2分别为测段起止点的大地纬度、大地经度。

2 固体潮改正变化规律分析

天体的视位置(赤经和赤纬)是每日每时每刻在变化的[14]且不呈线性变化，所以天体引潮力产生的固体潮在不同地点、不同时刻都不相同，即使在相同地点、不同时刻都是变化的。通过算例分析，掌握固体潮改正随观测时间(年、月、日)的变化规律，就可精密计算出水准测量时刻的固体潮改正值，有效保证水准测量的精度。

算例1：计算5 km测段在2020年5月1—31日每天00:00—24:00固体潮改正，绘制固体潮改正周日变化折线图(见图1)。

图1 固体潮改正周日变化折线图

从图1可以看出：每天固体潮改正随时刻变化呈周期性(正弦或余弦)变化(如2020年5月1—31日9 h)。

算例2：计算5 km测段在2020年1月—12月10日09:00固体潮改正，绘制固体潮改正月变化折线图(见图2)。

从图2可以看出：同年各日某一时刻每月固体潮改正变化均不同，同日同时的固体潮改正量总在某月达到最大值(如6日09:00固体潮在6月达最大值)、在某月(如12月)达到最小值，但从各月固体潮改正均值来看，5—8月较大，1月、12月最小，但3月、10月固体潮改正接近零，也就是说每年3月、10月的固体潮改正量较小。

图2 固体潮改正月变化折线图

算例3：计算5 km测段在2001—2021年5月10日09:00固体潮改正量，绘制固体潮改正年变化折线图(见图3)。

图3 固体潮改正年变化折线图

从图3可以看出：同月同日同时不同年固体潮改正呈周期性变化(周期约为4 a)。

3 测段高差固体潮改正计算方法

目前精密水准测量手簿一般只记录测段(两水准点间)往测、返测的始末时间，测段长度大约2～10 km，往测或返测的始末时间有同天、跨天、跨月甚至还有跨年的，而固体潮改正随观测时间(年、月、日)呈周期性变化，如果只用往测、返测的始末时间的固体潮改正均值代表往测、返测固体潮改正，计算方法太近似误差较大。由于固体潮改正与往、返测高差观测时刻有密切关系，改正值不但应按往、返测分别计算，应特别注意取用的观测时刻正确、合理[4]，还应充分顾及《规范》要求：水准观测不宜在日出与日落前30 min内、太阳中天前后各约2 h内进行[9]。对大量实测数据进行了分析和试验验证，提出文中论述的按测段计算往测、返测固体潮改正计算流程。

3.1 测段固体潮改正计算方法

《规范》要求：水准观测不宜在日出与日落前30 min内、太阳中天前后各约2 h内进行。全国各地日照时间大约为11 h(上午5.5 h、下午5.5 h)，除去日出与日落前的30 min，日照时间大约为10 h(上午5 h、下午5 h)，若再除去太阳中天前后各2 h，上午、下午有效观测时间约为3 h。从图1可以看出，固体潮改正随时刻呈周期性(正弦或余弦)变化。因此，文中采用分区段方法计算测段固体潮改正[11,15-17]，该方法充分考虑了最有利观测时间、间歇时间与休息时间，比直接用往测或返测的始末时间计算更为合理。计算方法描述如下：

1)往测或返测在同年、同月、同日观测。若(末时-始时)≤5 h时，则取始时、始末时中数、始末时中数、末时4个时刻的固体潮改正中数作为该测段的固体潮改正；若(末时-始时)>5 h时，分两个分段(上、下午)：第一分段取始时、始时+1.5 h、始时+1.5 h、始时+3 h这4个时刻的固体潮改正中数作为第一分段的固体潮改正，第二分段取末时-3 h、末时-1.5 h、末时-1.5 h、末时这4个时刻的固体潮改正中数作为第二分段的固体潮改正，然后取两分段的固体潮改正中数作为该测段的固体潮改正。

2)往测或返测在同年、同月、不同日(始末日不同)观测。取始日的始时、始时+1.5 h、始时+1.5 h、始时+3 h这4个时刻的固体潮改正中数作为始日的固体潮改正，取末日的末时-3 h、末时-1.5 h、末时-1.5 h、末时这4个时刻的固体潮改正中数作为末日的固体潮改正，然后取始、末两日的固体潮改正中数作为该测段的固体潮改正。

3)往测或返测在同年、不同月(始末月不同)观测。分两个分段(始月始日、末月末日)：取始月、始日的始时、始时+1.5 h、始时+1.5 h、始时+3 h这4个时刻的固体潮改正中数作为第一分段的固体潮改正，取末月、末日的末时-3 h、末时-1.5 h、末时-1.5 h、末时这4个时刻的固体潮改正中数作为第二分段的固体潮改正，然后取两分段的固体潮改正中数作为该测段的固体潮改正。

4)往测或返测在不同年(始末年不同)观测。分两个分段(始年始月始日、末年末月末日)：取始年、始月、始日的始时、始时+1.5 h、始时+1.5 h、始时+3 h这4个时刻的固体潮改正中数作为第一分段的固体潮改正，取末年、末月、末日的末时-3 h、末时-1.5 h、末时-1.5 h、末时这4个时刻的固体潮改正中数作为第二分段的固体潮改正，然后取两分段的固体潮改正中数作为该测段的固体潮改正。

3.2 算例验证

算例4：分别以2020年5月10日07：00—12:00、14:00—18:00、08:00—17:00、09:00—19:00这4个时间段用不同方法计算其固体潮改正U进行比较验证。计算结果统计见表1(表中Ut表示t时的固体潮改正)。

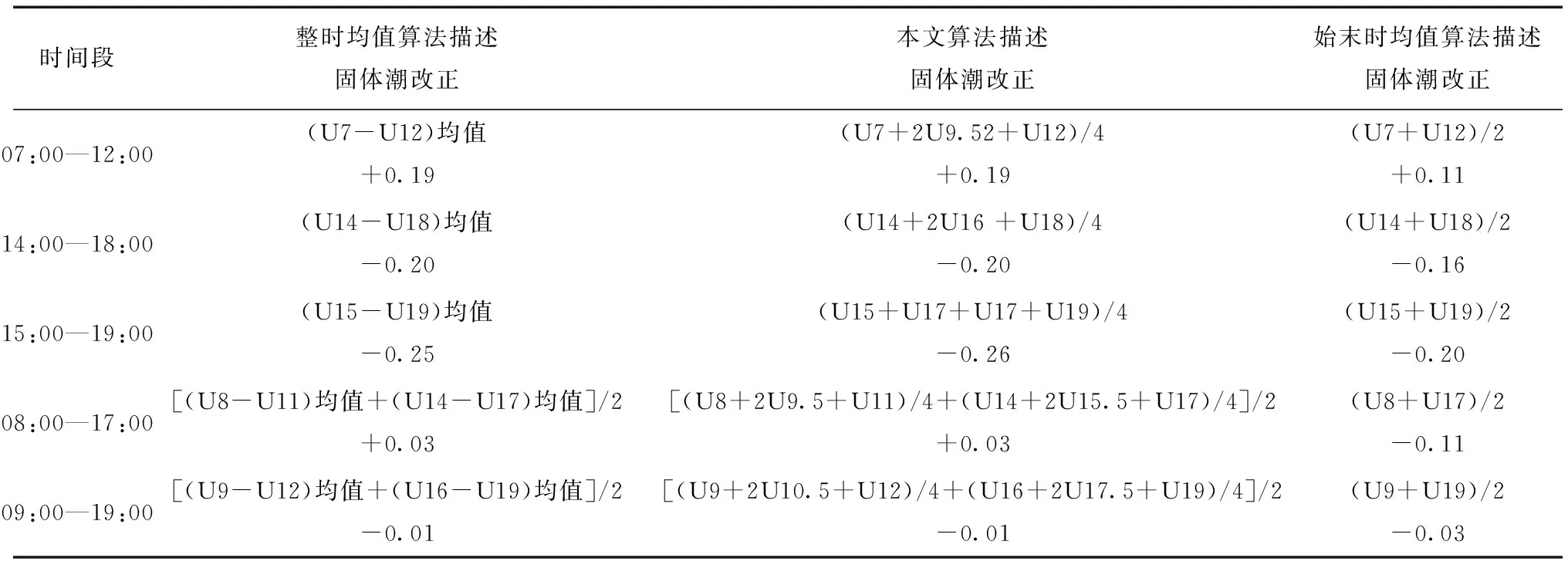
表1 不同方法计算的固体潮改正统计表 mm

从表1 可以看出：文中算法与考虑了最有利观测时间、间歇时间与休息时间的整时均值算法计算的测段固体潮改正基本一致，但直接采用始末时均值算法计算的固体潮改正误差较大，测段固体潮改正除用本文算法计算，还可以用整时均值算法计算。

4 基于测站的精密水准固体潮改正

固体潮改正大小是随着地球、太阳和月球的位置不同而不同的，三者的位置关系是时间的参数。就固体潮改正模型而言，它是水准测量在某地某瞬时时刻的固体潮改正，从固体潮改正的变化规律看，它是每日每时每刻在变化的(随日随时呈周期性变化)。目前《国家一、二等水准测量规范》中对精密水准测量的固体潮改正是按测段进行的，这给固体潮的改正带来了问题。测段上的固体潮的影响是每个测站上固体潮影响的积累，那么测段上固体潮改正本来应该是所有测站固体差改正的代数和。这种以测段来改正测站积累的固体差改正，残存误差很大，直接影响了改正效果[18]。鉴于此，文献[18-19]提出了基于测站的固体潮改正方案，文中用实际算例进一步验证了基于测站的固体潮改正方案的科学性与合理性。

算例5：分别选取2020年6月、10月、12月在云南施测的3条水准路线的3个水准测段数据(如图4所示)，对往测的高差分别以测段和测站为基本单元进行固体潮改正计算，比较结果如表2所示。

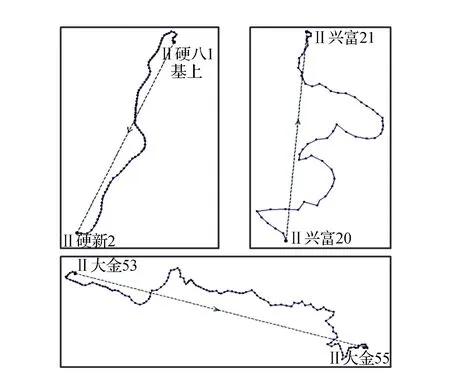
图4 水准测段示意

从表2可以看出：基于测段和测站的固体潮改正差异较大，如果累计到每条水准路线上，其差异将会更大。

表2 固体潮改正结果比较

通过实际试算，证明目前生产中普遍使用的按测段进行固体潮改正的方法残差较大，而按测站改正固体潮的方法比按测段进行固体潮改正精确得多，是今后精密水准测量中对固体潮改正的新思路。现代的水准测量自动化程度高，可同时精确记录每一动作的时间，且用GNSS 技术也可方便快捷获取每一测站点的坐标。因此，每个测站记录观测时刻和站点坐标信息，在每个测站进行固体潮改正，达到准确扣除固体潮影响的效果[19]。