几道2015年国外数学竞赛试题的巧思妙解



几道2015年国外数学竞赛试题的巧思妙解

江西省九江县新塘中学(332111)郤红英

本文旨在介绍笔者在中学数学解题教学中的亲身体会，期冀对各位老师有用、有益.

例1(2016年美国Mock ARML数学竞赛)

已知a+b=4,a2+b2=40,a2b+ab2=-48,求a3+b3+2ab的值.

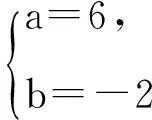
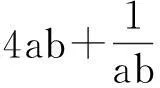
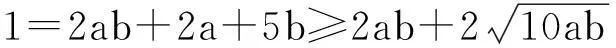
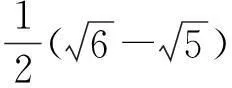
例3(2015年马来西亚数学竞赛)已知a,b,c≥3，求证：3(abc+b+2c)≥2(ab+2ac+3bc).

证明：3(abc+b+2c)-2(ab+2ac+3bc)

=(3bc-2b-4c)a+3(b+2c)-6bc

=3(c-1)b-6c≥9(c-1)-6c=3(c-3)≥0，故3(abc+b+2c)≥2(ab+2ac+3bc).

注：主元思想先导，减元操作随后. 比较法是证明不等式的最基本的方法.

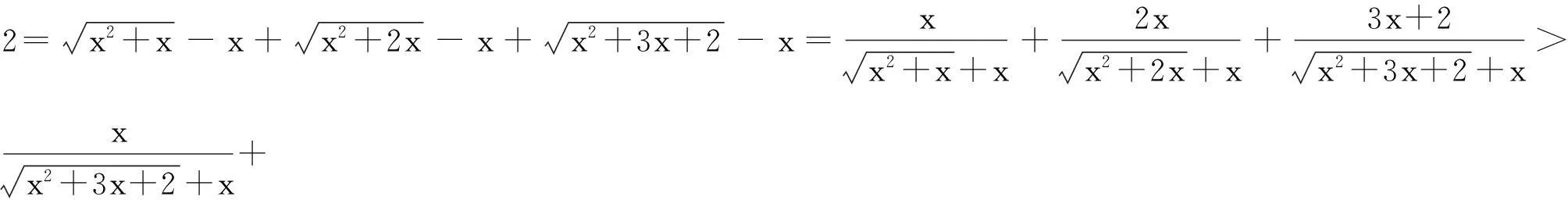
注：证明的第一步—变形—举足轻重，这是最困难的一步.所有工作的目标就是一个：获得二元不等式3x2+x-1<0.