构造等差数列解读无理方程组



构造等差数列解读无理方程组

江苏省泰州市姜堰区罗塘高级中学(225500)金岳男

本文主要谈谈如何构造等差数列解读某些非数列的无理方程组问题，供师生教学时参考.

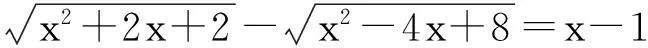
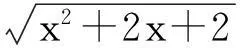
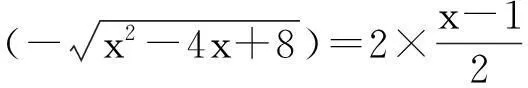
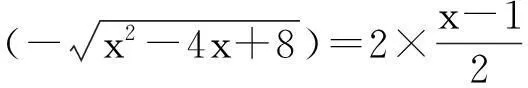
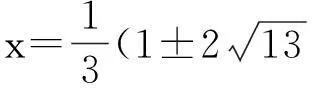
点评：本题解法的巧妙之处在于通过构造等差数列，大大减少了计算量，降低了解题的难度，可谓匠心独具，新颖别致.体现了解题的探索精神和创新精神，充分显示了构造法的优越性.

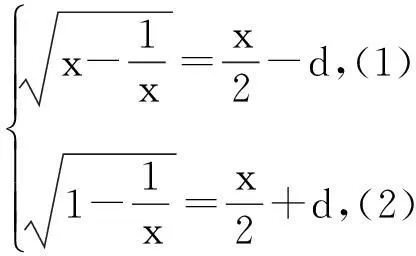
点评：本题用一般的思维方式考虑，很难找到解题的方法，而通过构造等差数列，沟通了题设与结论的关系，使问题得到轻松解决.此题从表面上看似乎与等差数列无关，使人陷入“山穷水尽疑无路”之情景.但仔细观察题目条件的特点，充分展开联想，发挥思维的创造性，使得解题思路简捷明快，解法简单顺畅，解法灵活巧妙.

思路分析：本题若采用平方法，对(1)式进行两次平方去掉根号求解，不仅运算复杂，而且也很困难.然而注意到(1)式的特征“两数之和是第三数”，应用构造等差数列的方法求解，可使问题化繁为简、变难为易.

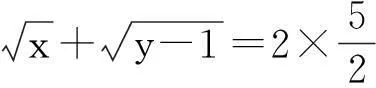
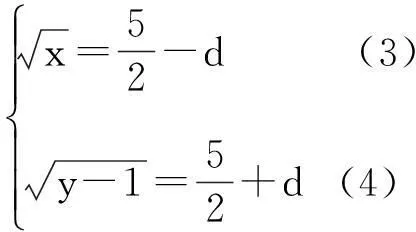
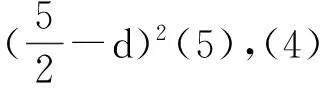
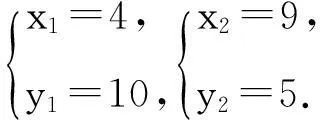
点评：本题解法的巧妙之处在于通过构造等差数列，避免了传统解法中脱根号的繁琐运算.

例4解方程组

思路分析：本题可采用平方法去根号求解，也可采用换元法求解.然而根据(1)式的特征，通过构造等差数列求解，却别有风味.

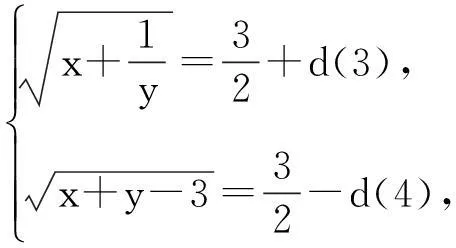
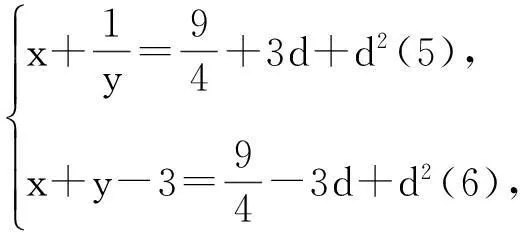
经检验上述四组解都是原方程组的解.

点评：本题按常规解法较繁较难，然而运用了构造等差数列法，则降低了解题难度，提高了解题速度，收到了意想不到的效果.

综上可知：例1例2均是先从已知方程变形入手，通过构造等差数列，设公差为d，再将所设两无理方程两边平方相减，求得公差d与x之间的关系式，最后将此关系式代回所设的无理方程中求得其解.例3例4均是从方程组中第(1)式入手，通过构造等差数列，设公差为d，将方程组中第(2)式变形为关于d的二次方程，求出d的数值后，进而求得方程组的解.构造等差数列解无理方程组，其关键是要从问题的背景出发，根据题目的结构特征，寻找两代数式之和等于第三个代数式的关系去构造等差数列.这种方法通俗易懂，它既有利于学生融会贯通“基础知识和基本技能”，又有利于帮助学生提高综合解题水平，对于启迪学生思维、开拓学生视野，提高教学质量，提高教师讲课效果，对于培养学生学数学、用数学、研究数学的兴趣均颇有益处.

参考文献

[1]马小燕.构造等差数列探究高考三角求值问题[J].数学教学通讯(重庆)，2010，9.