“充要条件”在数学求解中的错例分析



“充要条件”在数学求解中的错例分析

山东省泰安宁阳一中(271400)林令强

数学题目中的求解(证)结果是题目条件的必要不充分条件或者是充要条件.当题目中的求解(证)结果是题目给出的条件的必要不充分条件时，题目求解(证)结果只是由题目条件推出的多个结果之一，并未完整地表达出题目条件所具有的性质.当题目中的求解(证)结果是题目给出的条件的充要条件时，结果则完整地表达了题目条件所具有的性质.若我们求解(证)的题目结果是条件的充要条件，在求解时，要么保证解题过程等价，要么先求出题目条件的必要条件，然后进行验证，以保证结果与条件等价.笔者结合教学经验，谈几例学生因对题目的求解(证)结果与题目条件关系不明确而引发的错误，以飨读者.

错因：f(0)=0是f(x)是奇函数的必要不充分条件，故得出的结果不能保证f(x)是奇函数.

正解：解法一(解题过程等价)

解法二(先求条件的必要条件，再验证)

例2定义在R上的函数f(x)满足f(x+2)+f(x)=0，且函数y=f(x-1)是奇函数，则函数f(x)的图像可能是().

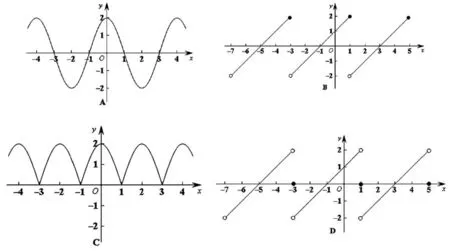
错解：由f(x+2)+f(x)=0，可类比得f(x+4)+f(x+2)=0，所以f(x+4)=f(x)，T=4.因为y=f(x-1)是奇函数，即y=f(x-1)的图像关于点(0,0)成中心对称，所以y=f(x)的图像关于点(-1,0)成中心对称.故选D.

错因：f(x+2)+f(x)=0能推出T=4，但T=4推不出f(x+2)+f(x)=0，即T=4是f(x+2)+f(x)=0的必要不充分条件，所以由T=4推出的函数图像并不能完整的表达f(x+2)+f(x)=0所具有的性质.

正解：解法一(解题过程等价)

函数y=f(x-1)是奇函数，所以f(-x-1)=-f(x-1)，由f(x+2)=-f(x)得-f(x-1)=f(x+1)，所以f(-x-1)=f(x+1)，所以f(-x)=f(x)，于是得函数f(x)为偶函数，又由f(x+2)+f(x)=0可类比得f(x+4)+f(x+2)=0，所以f(x+4)=f(x)，T=4，故选A.

解法二(图像变换)

f(x+2)+f(x)=0，当x∈(-2,0)时，x+2∈(0,2)，因为满足f(x+2)=-f(x)，显然只有A满足条件，故选A.

(1)当a=1时，证明：函数y=f(x)在(0,+∞)上是增函数；

(2)若y=f(x)在(0,+∞)上是增函数，求正数a的取值范围.

错因：很显然“a≥1是y=f(x)在(0,+∞)上是增函数的必要条件”，解法并没有说明a≥1能使函数y=f(x)在(0,+∞)上是增函数.