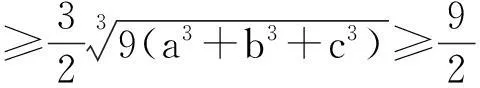分拆方法在证明不等式中的应用例谈



分拆方法在证明不等式中的应用例谈

南昌大学附属中学(330047)周辉

分拆在不等式的证明中非常重要.分拆的目的就是为使用常用的不等式营造一个和谐的环境.下面笔者以2015年国际数学奥林匹克的一些典型试题为例，充分展示分拆方法在证明不等式中的作用.

例1(2015年阿塞拜疆数学奥林匹克)

评注：合理的分拆，为放缩和应用柯西不等式创造了条件.

例2(2015年澳大利亚数学奥林匹克)

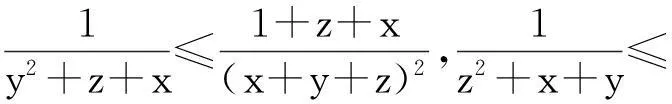
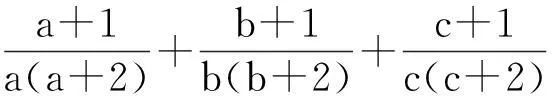
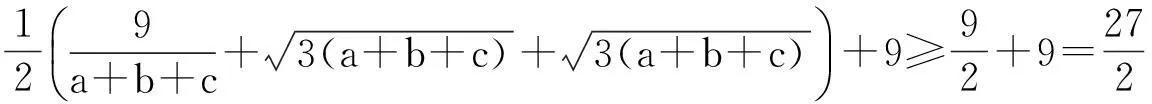
评注：多项的分拆放缩，目标是使取等的条件一致.

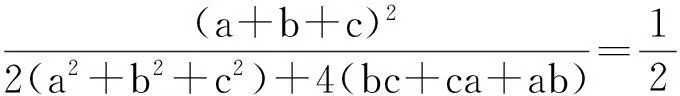
综上，原不等式成立.

评注：第一次的分拆，是将分母升幂，为后续的换元打下基础.

例6(2015年阿塞拜疆数学奥林匹克)

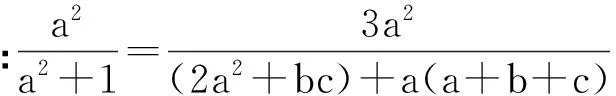
例7(2015年摩尔多瓦数学奥林匹克)已知a,b,c是满足abc=1的正数,求证：