一类高考压轴题中的不等式证明策略
2016-05-05缪林
一类高考压轴题中的不等式证明策略
江苏省昆山中学(215300)缪林
在各地高考压轴题中常见这样的不等式“a1+a2+…+an>F(n)”或“ a1·a2·…·an>F(n)”的判断或论证,这类问题涉及函数、数列、不等式等综合知识,对数学知识技能、数学思想意识的要求非常之高. 命题意图是对前面几个小问中获得的结论进行“二次开发”,获得一个新的命题,再利用这一命题进行论证,解题技巧强,思维要求高,因此,绝大多数同学望而却步. 若从“看成”角度探寻解题策略,常常可以化难为易迎刃而解.
所谓 “看成”即是通过对数学问题表征的分析研究,将数学对象赋予(视着)新的数学意义,并尝试将其激活为某类问题模型的过程. “看成策略”即是在“看成”的基础上选择解题方向,拟定解题计划,然后执行相应的解题程序.这是一种有目的的思维活动,但并不遵循严格的规则,通常是凭知识经验和审美判断,带有一定程度的猜测性和预见性,常常需要多角度尝试“看成”,合理“看成”路径的选择是解题成功的关键.
1、将F(n)看成数列前n项之和
例1(2014年陕西(理)第21题) 设函数F(x)=ln(1+x),G(x)=xF ′(x),x≥0,其中F ′(x)是F(x)的导函数.
(1)令G1(x)=G(x),Gn+1(x)=G(Gn(x)),n∈N+,求Gn(x)的表达式;
(2)若F(x)≥aG(x)恒成立,求实数a的取值范围;
(3)设n∈N+,比较G(1)+G(2)+…+G(n)与n-F(n)的大小,并加以证明.
思路探求:(1),(2) 两小问略;
由于S(n)是数列{G(n)}的前n项之和,故可尝试把T(n)看成数列{bn}前n项之和,若能比较G(n)与bn之大小即可获得结论.

评析:对问题表征的差异分析是实现“看成”的关键. 左式是n项之和,而右式仅二项,减少差异的两种最为自然的想法是:其一、对左式求和——“合”,但在此处显然是不可能的;其二、将右式转化为某数列前n项之和——“分”,由此获得“看成”的策略:将T(n)看成某数列前n项和,进而将问题转化为比较两数列相应项的大小,这远比创造性地运用第(2)小问获得的结论,通过对左式中的通项进行放缩转化为可求和的数列进行求和再比较大小更为简捷明晰.
2、将F(n)看成数列前n项之积
例2(2015年安徽理科题)设n∈N*,xn是曲线y=x2n+3+1在点(1,2)处的切线与x轴交点的横坐标.
(1)求数列{xn}的通项公式;





3、将“常数”看成无穷递缩等比数列所有项之和或数列的前n项之和
例3(2014新课标理科Ⅱ理)已知数列{an}满足a1=1,an+1=3an+1.
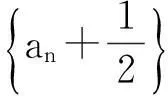

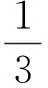

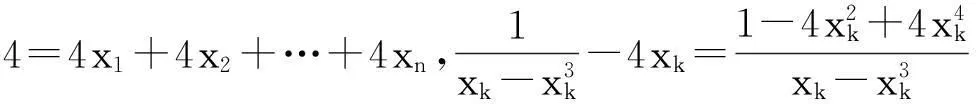
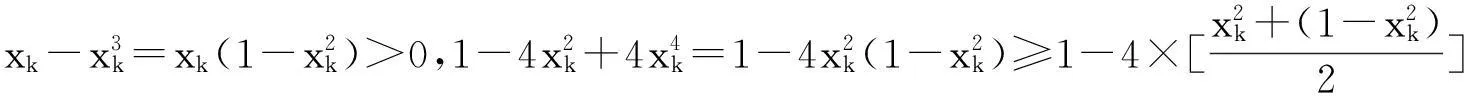


在差异分析观点之下,上述措施不是一个妙手偶得的特殊技巧,而是一个策略思想的具体实施.
参考文献
[1]罗增儒. 数学解题学引论[M]. 西安:陕西师范大学出版社,1997.
[2]齐建民. 从“见山是山”到“见山不是山”[J]. 中学数学研究(江西),2014(4):28-30.
[3]缪林. 目标引领 理性探索[J]. 中学数学教学参考,2011(11):37-40.
